使用Latex插入数学公式(二)
初级运算
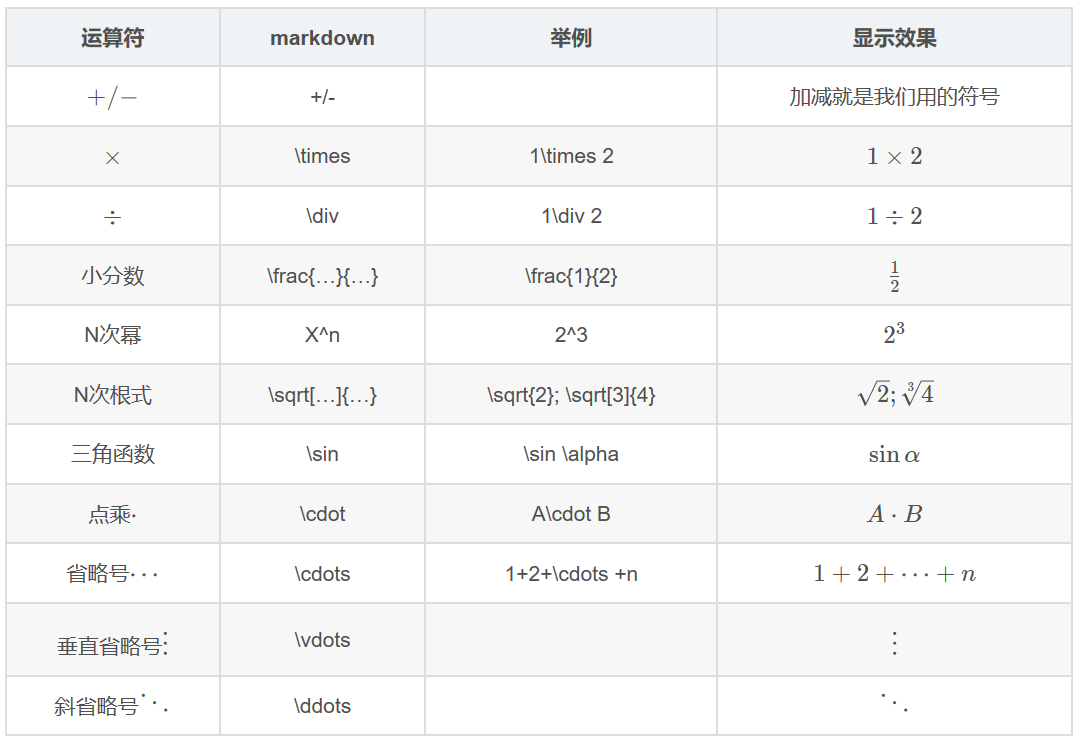
关系运算符

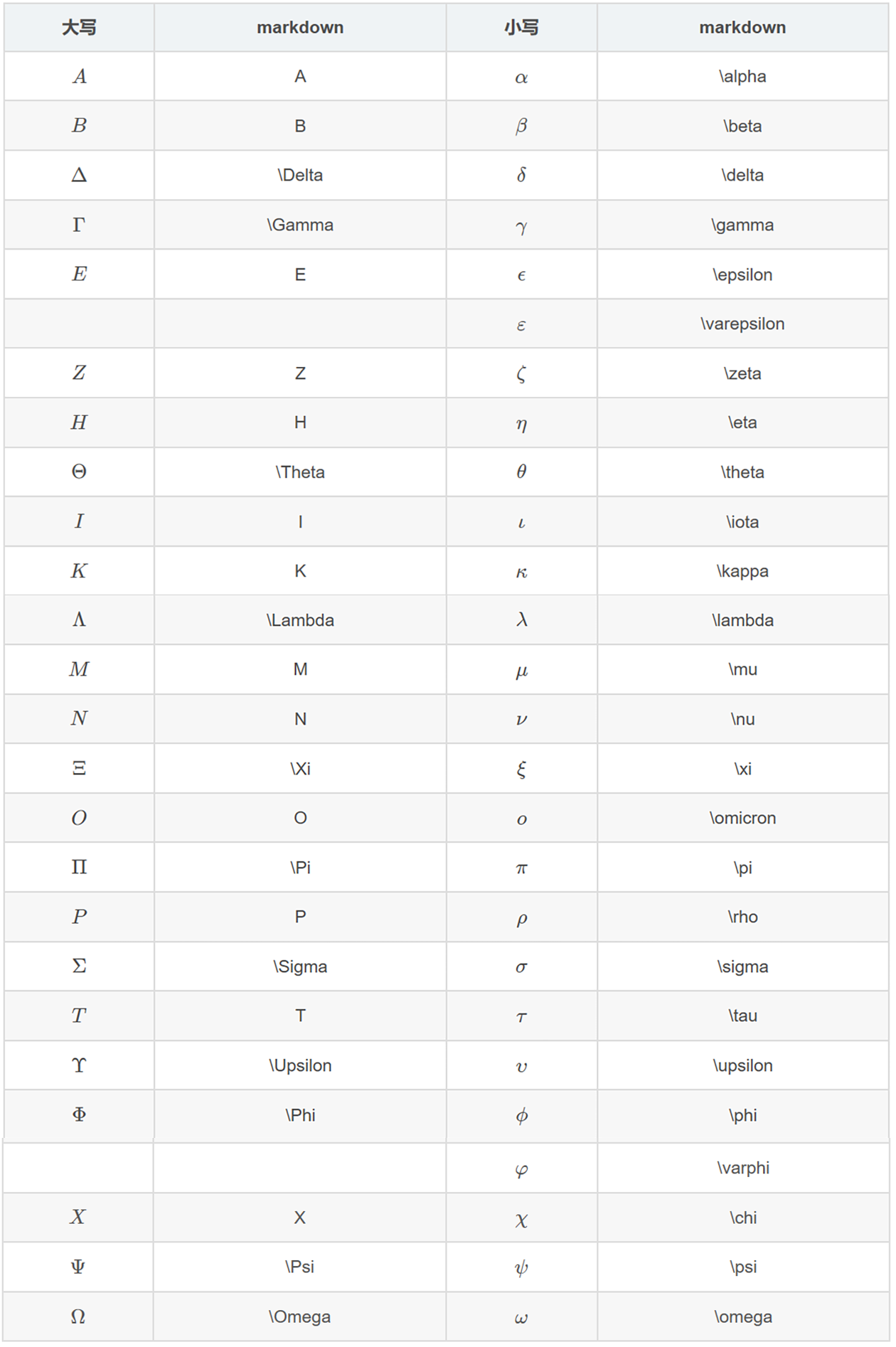
希腊字母
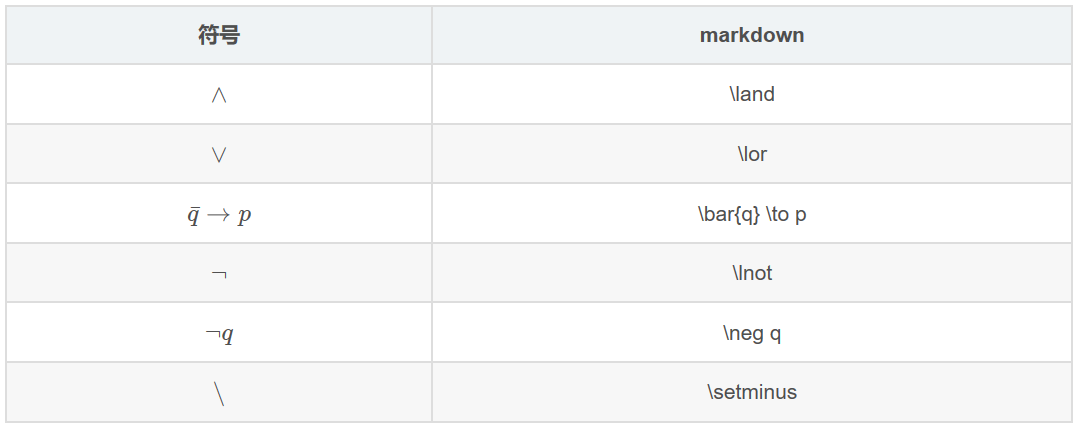
集合运算符 逻辑运算符
逻辑运算符
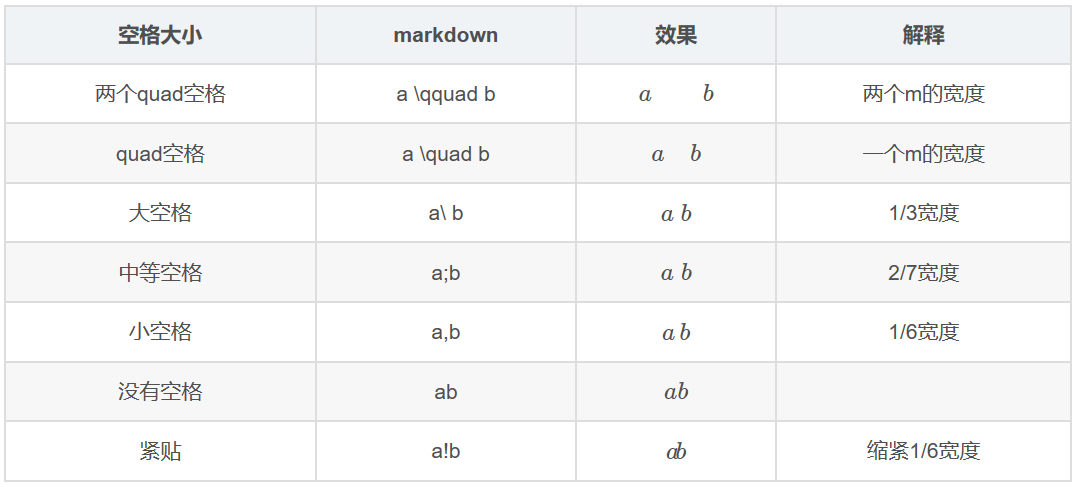
空格问题
矩阵格式
矩阵格式有三种:
- 无括号的矩阵
matrix 是 Latex 的矩阵命令,矩阵命令中每一行以 \\ 结束,矩阵的元素之间用 & 来分割开
$$
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix} \tag{1}
$$
$$
\begin{matrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{matrix} \tag{1}
$$
- 中括号的矩阵
$$
A=
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{bmatrix} \tag{2}
$$
$$
A=
\begin{bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{bmatrix} \tag{2}
$$
- 花括号的矩阵
$$
A=
\begin{Bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{Bmatrix} \tag{3}
$$
$$
A=
\begin{Bmatrix}
1 & 2 & 3 \\
4 & 5 & 6 \\
7 & 8 & 9
\end{Bmatrix} \tag{3}
$$
分段函数
$$k_j=\begin{cases}
1 & knet_j=max\left\{knet_1,knet_2,\cdots,knet_h\right\}\\
0 & 其他\\
\end{cases}$$
$$k_j=\begin{cases}
1 & knet_j=max\left\{knet_1,knet_2,\cdots,knet_h\right\}\\
0 & 其他\\
\end{cases}\tag{4}$$
连分式
$$\begin{aligned}
b_0+
\cfrac{a_1}{b_1 +
\cfrac{a_2}{b_2 +
\cfrac{a_3}{b_3 +
\ddots
\cfrac{a_n}{b_n}}}}
\end{aligned}$$
$$\begin{aligned}
b_0+
\cfrac{a_1}{b_1 +
\cfrac{a_2}{b_2 +
\cfrac{a_3}{b_3 +
\ddots
\cfrac{a_n}{b_n}}}}
\end{aligned}\tag{5}$$
一个技巧
如果你的等式需要写多步,将等号对齐会好看的多。& 用于对其等号等符号,以编排格式(&本来是用来分割单元的,但系统会自动将&分割出的列自动排版)。
$$
\begin{aligned}
knet_j & =XW_j\\
&=(x_1,x_2,\cdots,x_n){(w_{1j},w_{2j},\cdots,w_{nj})}^T\\
&=w_{1j}x_1+w_{2j}x_2+\cdots+w_{nj}x_n
\end{aligned}$$
$$
\begin{aligned}
knet_j & =XW_j\\
&=(x_1,x_2,\cdots,x_n){(w_{1j},w_{2j},\cdots,w_{nj})}^T\\
&=w_{1j}x_1+w_{2j}x_2+\cdots+w_{nj}x_n
\end{aligned}\tag{6}$$
行间有效
可以使用 \displaystyle,
也就是单独占一行的公式的格式,与之相对应的是inline格式也就是行内公式。
$\sum_{i=1}^ni^2 + 1$
$\displaystyle \sum_{i=1}^ni^2 + 1$
- $\sum_{i=1}^ni^2 + 1$
- $\displaystyle \sum_{i=1}^ni^2 + 1$
参考链接:
(1)https://blog.csdn.net/GloriousEzreal/article/details/80748658#_266
(2)https://blog.csdn.net/bennyfun79/article/details/15500575
(3)https://blog.csdn.net/yanxiangtianji/article/details/17583723


 浙公网安备 33010602011771号
浙公网安备 33010602011771号