用球面映射巧解分赃难题：拓扑学的另一妙用
问题
一条项链上有n种类型的珠宝，每种珠宝的数量均为偶数。问至少可以切多少刀，可以将所有珠宝均分？
首先介绍Borsuk-Ulam Theorem:
想象一个三维空间中的球面被扭曲压缩到二维平面上，由于变形是连续的，因此球面上有许多点重合在了一起。
$Borsuk-Ulam$定理告诉我们，总能找到这样的两个点，它们一开始在球面上处于完全相反的两极，经过映射后会重新合在一起。
这个定理有一个经典的应用：地球上一定存在完全相对的某一对点，两处的气温和气压都恰好相同。因为地球上每一点都对应这气温和气压两个值，这与将地球表面映射到一个二维平面是一样的，同时这映射也是连续的。
简单证明
给定某个从球面到平面的函数，想象地球赤道上两个相对的点问绕赤道走一圈，则函数在平面上相应的函数值会形成某种闭合回路，由于两点最后一定交换了位置，那么一定存在使这两点的$X$坐标相同的位置，标记下这一位置。
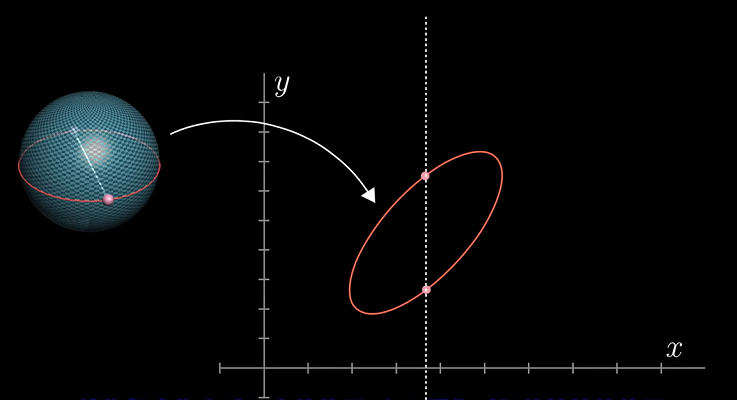
想象将赤道倾斜，沿着这个略微不同的圆继续上述步骤，此时在平面上输出的回路会有所改变，不过同理，在路线上一定存在某点使得对拓的两点$X$坐标相等，标记下这一位置。
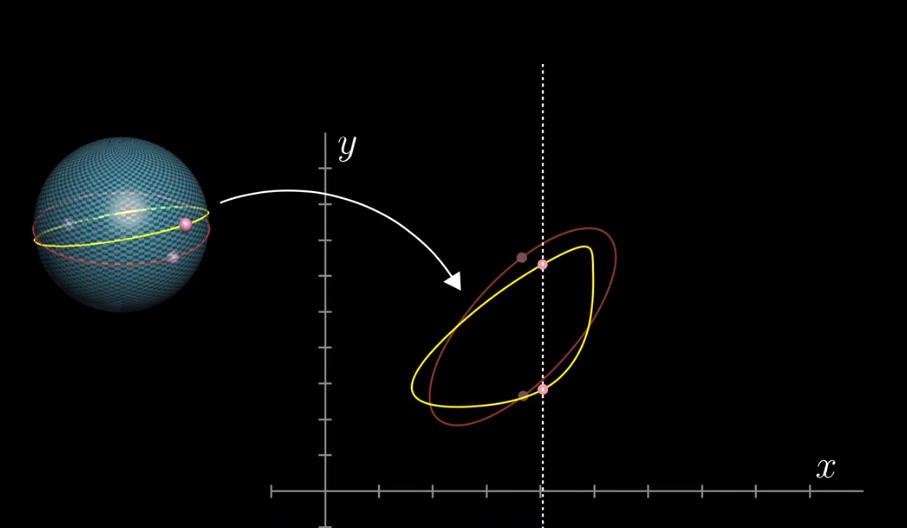
重复这一步骤，连续旋转赤道，经过180°，回到原位。你所标记的点在球面上会形成闭合回路。所标记的点在平面上同样形成闭合回路（白色线条所示），在这条回路上，这两点的$X$坐标总是相同的，同时由于两点最后也会交换位置，因此中途定有一点使得$Y$坐标也相等。这样我们就找到了这一点。
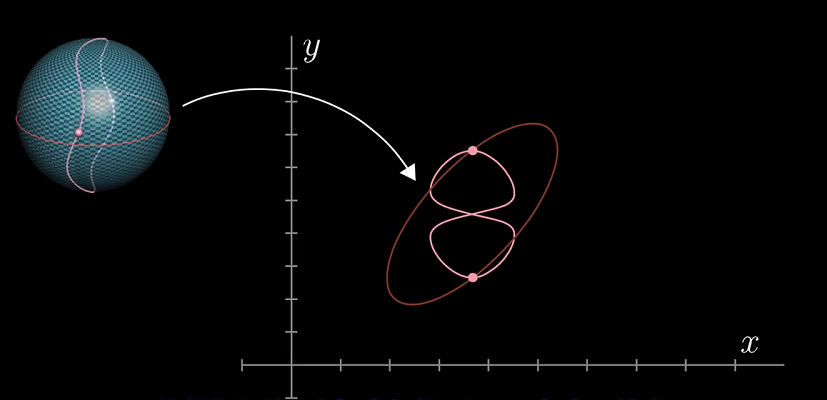
为了阐述该定理如何应用到我们的问题上，首先将$Borsuk-Ulam$定理严格写出
$$\text{For any continuous function } f: S^2\rightarrow \mathbb{R}^2 \\
\exists (x_1,x_2,x_3) \qquad\text{s.t. } x_1^2+x_2^2+x_3^2=1 \\
f(x_1,x_2,x_3) = f(-x_1,-x_2,-x_3)$$
由于该定理适合于连续情况而项链分赃问题是离散的，首先将宝石想象成连续的线段。可以看出如果这一连续的问题能够解决，则离散的问题也自然解决。因为我们可以调整切割点的位置使其恰好落在线段的端点上。
考虑仅有2中宝石的情况，令项链长度为1，欲将球的方程与切割方法联系起来，令切割的三段长度分别为$x^2,y^2,z^2$，并根据正负号将这一长度分给$A$或$B$比如系数为正，则这一段给贼1；系数为负，则一段给贼2
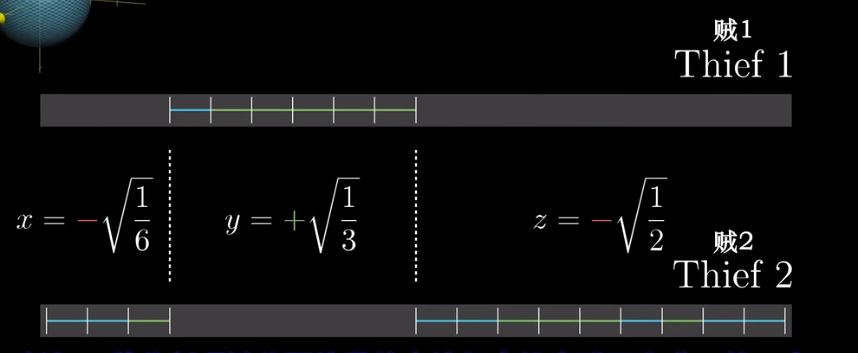
这样就有$x^2+y^2+z^2=1$，即球面上的每一点对应一种分配方案。
更进一步地，我们构造这样的函数：输入一个给定的项链分配方案，输出两个数，分别对应其中一人得到的两种宝石数量。这其实就是从球面到平面的一个映射。由$Borsuk-Ulam$定理可知，一定存在一种分配方案使得$A、B$在交换所分得的宝石后保持每种数量不变，也就是一种均分方案。
将这一定理拓展至高维情形：从一个$n$维空间的超球面到$n-1$维空间的映射也必须保证这样一对点存在。因此对于$n$种不同的宝石，只需要切$n$刀便可均分。
参考链接
