文法与文法分类
文法
文法的定义
文法:文法是定义和阐明语言的一种规格化方法,也可以说是以有穷的集合刻画无穷的集合的一种工具
20世纪50年代,美国语言学家乔姆斯基提出一个短语结构文法,同时还根据产生语言的文法的产生式的不同将文法和对应的语言分为三大类
一个短语结构文法(grammer)(简称)文法G包括:
- 一个有限集合N,其元素称为非终结符号
- 一个有限集合T,其元素称为终结符号
- {(N∪T)* - T*} x (N∪T)* 的一个有限子集P,称为产生式的集合
- 一个开始符号σ∈N
记作G=(N,T,P,σ)
产生式:产生式(α,β)∈P通常写成α→β。在产生式中a∈(N∪T)* - T*,于是α至少包含一个非终结符号,而β能够由终结符号和非终结符号的任意组合构成。
α称为这个产生式的左部,β称为这个产生式的右部
文法的推导
(1)设G=(N,T,P,σ)是一个文法,如果α→β是一个产生式且xαy∈(N∪T)* ,这里x,y∈(N∪T)* ,则称xβy可直接从xαy推导,并写成xαy=>xβy
(2)如果对于αi∈(N∪T)*(i=1,2,...,n),都有αi+1∈(N∪T)*(i=1,2,...,n-1)可直接从αi推出,则称αn可从α1推导,并写成αn=>α1,我们称α1=>α2=>...=>αn是αn的推导
一个约定:(N∪T)*的任意元素都是自身可推导的。w∈T*称为文法正确的当且仅当σ=>w
可见推导是是(N∪T)*上的关系,而且具有传递性
注意,“文法正确”不一定“语意正确”
文法到语言
由文法G生成的语言是指σ可推导的T上所有字符串组成的集合,记作L(G)
例如:
(1)文法G=({σ},{x},{σ→xσ,σ→x},σ)生成的语言是L(G)={xn | n≥1}
(2)文法G=({σ},{x},{σ→xσ,σ→λ},σ)生成的语言是L(G)={xn | n≥0}
(3)文法G=({σ},{x},{σ→xσy,σ→xy},σ)生成的语言是L(G)={xnyn | n≥1}
文法的等价
如果L(G)=L(G’),则称文法G和G’等价
例如:
(1)文法G=({σ},{x},{σ→xσ,σ→x},σ)生成的语言是L(G)={xn | n≥1}
(2)文法G=({σ},{x},{σ→σx,σ→x},σ)生成的语言是L(G)={xn | n≥1}
这两个语言相同,所以这两个文法等价
文法的分类
设G=(N,T,P,σ)是一个文法并设λ是空串。
- 产生式的两端无任何限制的为0型文法,0型文法产生的语言称为0型语言或称递归可数语言
- 如果每个产生式σAβ→αδβ,其中α,β∈(N∪T)*,A∈N,δ∈(N∪T)*-{λ}。则称G为上下文相关(1型)文法
- 如果每个产生式为A→δ,其中A∈N,δ∈(N∪T)*,则称G为上下文无关(2型)文法
- 如果每个产生式形式为A→a或A→aB或A→λ,其中A,B∈N,a∈T,则称G为正则(3型)文法
为什么“1型”文法称为上下文相关文法?
在上下文相关文法中,产生式σAβ→αδβ表明只有当非终止符号A的前后为α、β的条件下(即所谓的“上下文”),A才可以改写成δ
而在上下文无关文法中,产生式A→δ表明任何时候都可以将A替换成δ.
正则文法的产生非常简单,右部为一个终结符号、一个终结符号跟一个非终结符号或者为一个空串
例如:
(1)设N={σ,A,B,C,D,E},T={a,b,c},P={σ→aB,A→aAC,CD→CE,Cc→Dcc},则G={N,T,P,σ}是一个上下文相关文法
(2)G=({σ},{0,1,+,x},{σ→0,σ→1,σ→σ+σ,σ→σxσ}P,σ)是一个上下文无关文法
(3)可以证明L(G)={anbncn | n≥1}不是正则的
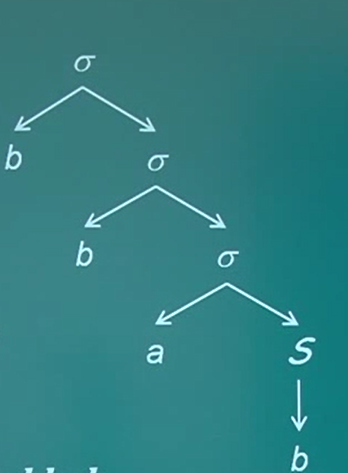
(4)N={σ,S},T={a,b},P={σ→bσ,σ→aS,S→bS,S→b},则G={N,T,P,σ}是一个正则文法
分析树
分析树(parse tree),也称作派生树或具体语法树,它使用位置根树的形式描述一个上下文无关文法中句子的推导结果
假设G={N,T,P,σ}是一个上下文无关文法。则
- 对树中的每一个顶点使用N∪T中的一个符号进行表示
- 跟的标号为σ
- 树的叶子结点都是终结结点
- 树的非叶子结点都是非终结结点
- 若顶点A的子女结点从左到右依次B1、B2、... 、Bn,则必有产生式A→B1B2...Bn
- 从左到右读出每个叶子节点的标号
例如:
正则文法G=(N,T,P,σ),N={σ,S},T={a,b},P={σ→bσ,σ→aS,S→bS,S→b},易知这是一个上下文无关文法
从σ唯一推导的是
$\sigma =>b\sigma =>...=>b^n\sigma \\=>b^naS=>...=>b^nan^{m-1}S\\=>b^nab^m$
看一个具体的例子字符串bba可从σ可推导的,写成
$\sigma =>b\sigma =>...=>b^n\sigma \\=>b^naS=>...=>b^nan^{m-1}S\\=>b^nab^m$
所以它的分析树如下:
歧义文法
设G=(N,T,P,σ)是一个上下文无关文法,若存在x∈L(G),使得有两个(或两个以上)的分析树可以产生x,则称G为一个有歧义的文法,简称为歧义文法。
有定理表明:上下文无关文法是否有歧义性是不可判定的。
1961年帕克里(Rohit Parikh)证明一些文法具有固有的歧义性,即每个与之等价的文法都是歧义文法。
参考资料:中国大学mooc 刘铎 离散数学


 浙公网安备 33010602011771号
浙公网安备 33010602011771号