谢宾斯基三角形的几种生成方法
简介
谢宾斯基三角形(Sierpinski triangle)是一种分形,由波兰数学家谢宾斯基在1915年提出。它是一种自相似集。

几种生成方法
方法一:去掉中心
- 取一个实心的三角形(多数用等边三角形)
- 连接三边中点,将它们分成4个小三角形
- 将正中间的三角形挖空
- 对其余三个小三角形重复操作1

取一个正方形或其它图形开始,用类似的方法,形状也和谢宾斯基三角形相似,例如:
- 取一个实心正方形
- 将它分成3个“品”字形的小正方形
- 将其余部分“挖空”
- 重复步骤1

方法二:Chaos Game
- 任取平面上三点,画出这三点
- 在平面上任取一点P
- 画出P与三角形其中任意一个顶点的连线的中点
- 重复2
这种方法简单暴力,但又极其优雅。

1 / 程序名称:谢宾斯基(Sierpinski)三角形,也叫垫片 2 // 编译环境:Visual C++ 6.0,EasyX 2011惊蛰版 3 // 最后更新:2010-11-16 4 // 5 #include <graphics.h> 6 #include <conio.h> 7 #include <time.h> 8 9 int main() 10 { 11 srand((unsigned)time(NULL)); // 设置随机种子 12 POINT P[3] = {{320, 50}, {120, 400}, {520, 400}}; // 设定三角形的三个顶点 13 POINT p = {rand() % 640, rand() % 480}; // 随机产生当前点 14 15 // 初始化图形模式 16 initgraph(640, 480); 17 18 // 绘制三万个点 19 int n; 20 for(int i = 0; i <= 30000; i++) 21 { 22 n = rand() % 3; 23 p.x = (p.x + P[n].x) / 2; 24 p.y = (p.y + P[n].y) / 2; 25 putpixel(p.x, p.y, GREEN); 26 } 27 28 // 按任意键退出 29 getch(); 30 closegraph(); 31 32 return 0; 33 }
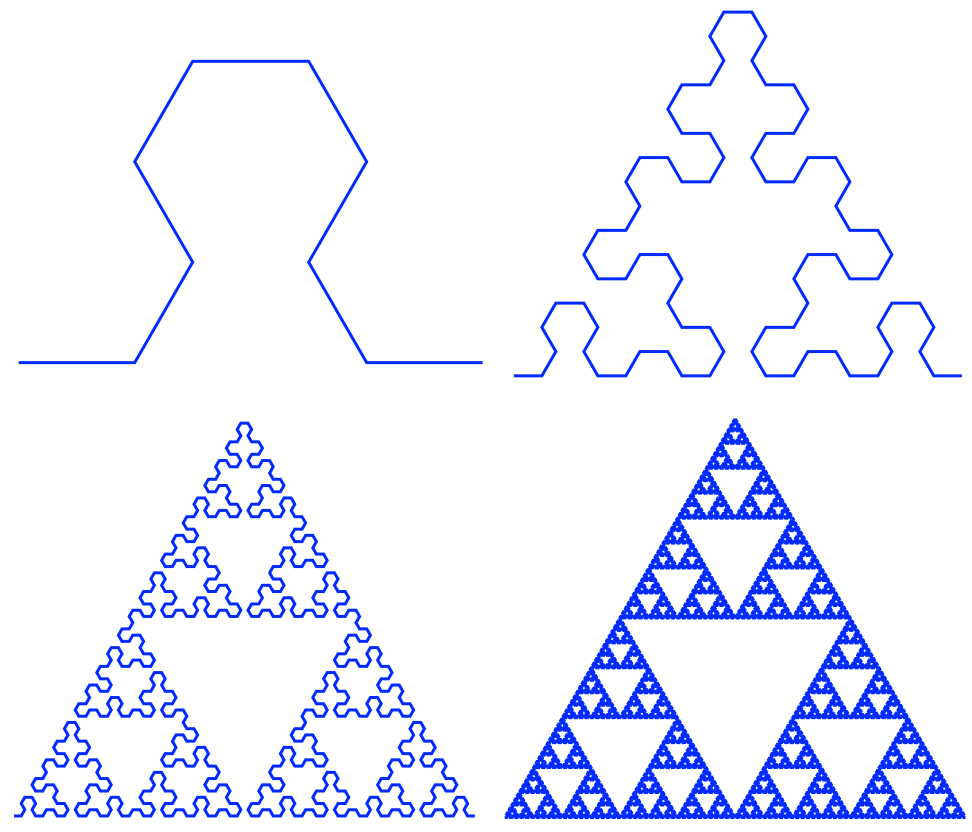
方法三:L系统
通过曲线逼近谢宾斯基三角(没看懂维基上的生成规则,555)
贴图:
方法四:杨辉三角
将有4·2n(n≥0) 行的杨辉三角中的奇数染成黑色,当n趋于无穷大时,得到的就是谢宾斯基三角形
例如:n=3时

方法五:元胞自动机
也译作细胞自动机,由冯·诺依曼在20世纪50年代,此后史蒂芬·沃尔夫勒姆对元胞自动机理论作了深入的研究。
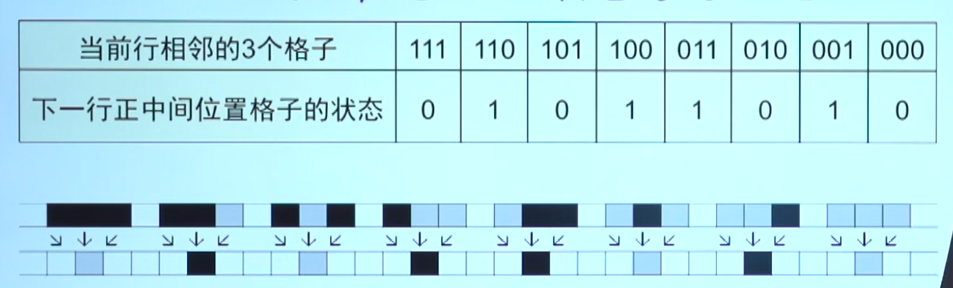
元胞自动机有很多规则,这里用“规则90”
考虑无限长度的一维格子表,用黑色格子表示1,白色格子表示0,有无限行这样的一维格子表就形成了“只有上界”的二维格子表。
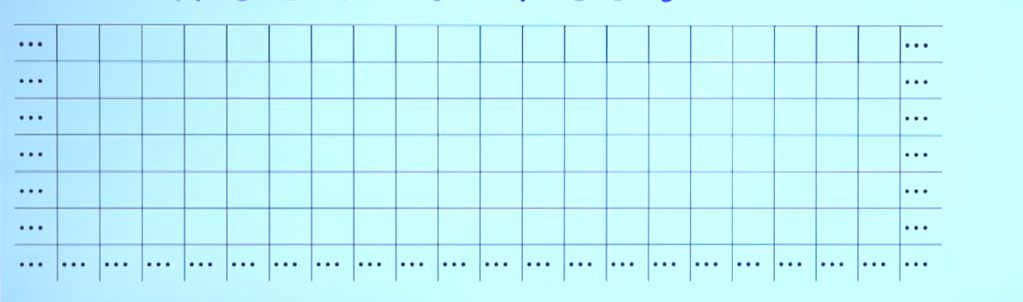
“规则90”:相邻的三个格子决定下一行中间格子的状态,具体规则如下表:
生成的过程:

其实从从杨辉三角来理解这种方法就不难了。
分形
1973年,曼德勃罗(B.B.Mandelbort)首次提出分维和分形(fractal)的设想,其原意具有不规则和支离破碎的几何形状。一般是指“一个粗糙或零碎几何形状,可以分成数部分,且每一份(大约)是整体的缩小版”,此性质称为“自相似”。
数值特征
例如:用无限的周长围住了面积为0的区域
例如:在谢宾斯基三角形中,设初始周长为1单位,初始面积为1单位,则有$S_n=/frac{3}{2}^n$,$C_n=/frac{3}{4}^n$。当n趋于无穷大时,周长为∞,面积为0.
维数(豪斯多夫维)
例如:当一个正方形边长变成3倍时,得到9个他组成的、和它相似的正方形,正方形的维数是2,恰好又$log9/log3=2$
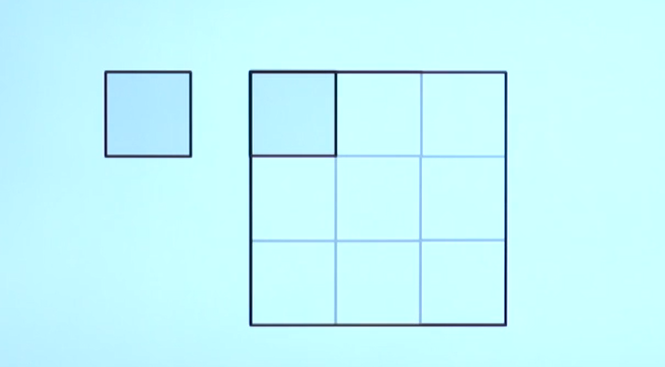
又例如:当一个长方体边长变成2倍时,得到8个由它组成、与它相似的长方体,长方体的度数为3,恰好有$log8/log2=3$

而谢宾斯基三角形的边长变成2倍时,得到三个由它组成、与它相似的图形,根据前面的计算方法,它的豪斯多夫维是$log3/log2\approx 1.585$,不再是整数。
结语
学习《离散数学》看到谢宾斯基三角形,发现POJ1942就是有关它的题目。这样有成功的水一题(可还行)。

1 #include<cstdio> 2 #include<algorithm> 3 using namespace std; 4 5 const int maxm = (1 << 10) + 10; 6 const int maxn = (1 << 11) + 10; 7 char ch[maxm][maxn]; 8 int n; 9 10 inline void draw(int x, int y, int n) 11 { 12 if (n == 1) 13 { 14 ch[x][y] = '/'; ch[x][y + 1] = '_'; ch[x][y + 2] = '_'; ch[x][y + 3] = '\\'; 15 ch[x - 1][y + 1] = '/'; ch[x - 1][y + 2] = '\\'; 16 return; 17 } 18 draw(x, y, n - 1); 19 draw(x, y + (1 << n),n - 1); 20 draw(x - (1 << (n - 1)), y + (1 << (n - 1)), n - 1); 21 } 22 23 void solve() 24 { 25 while (scanf("%d",&n) == 1 && n) 26 { 27 int row = 1 << n, col = 1 << (n + 1); 28 for (int i = 0; i < row; i++) 29 for (int j = 0; j < col; j++) ch[i][j] = ' '; 30 draw(1 << n, 0, n); 31 for (int i = 1; i <= row; i++) 32 { 33 int last; 34 for (int j = 0; j < col; j++) if (ch[i][j] != ' ') last = j; 35 for (int j = 0; j <= last; j++) printf("%c", ch[i][j]); 36 printf("\n"); 37 } 38 printf("\n"); 39 } 40 } 41 42 int main() 43 { 44 solve(); 45 46 return 0; 47 }
参考链接:
2、https://www.cnblogs.com/ljh2000-jump/p/5883295.html
3、https://www.codebus.cn/yangw/post/sierpinski-triangle



 浙公网安备 33010602011771号
浙公网安备 33010602011771号