计算机组成与设计(五)—— 加法器的优化
4-bit加法器示例
先看一下上一节得到的加法器实现,可以看出改进的地方。
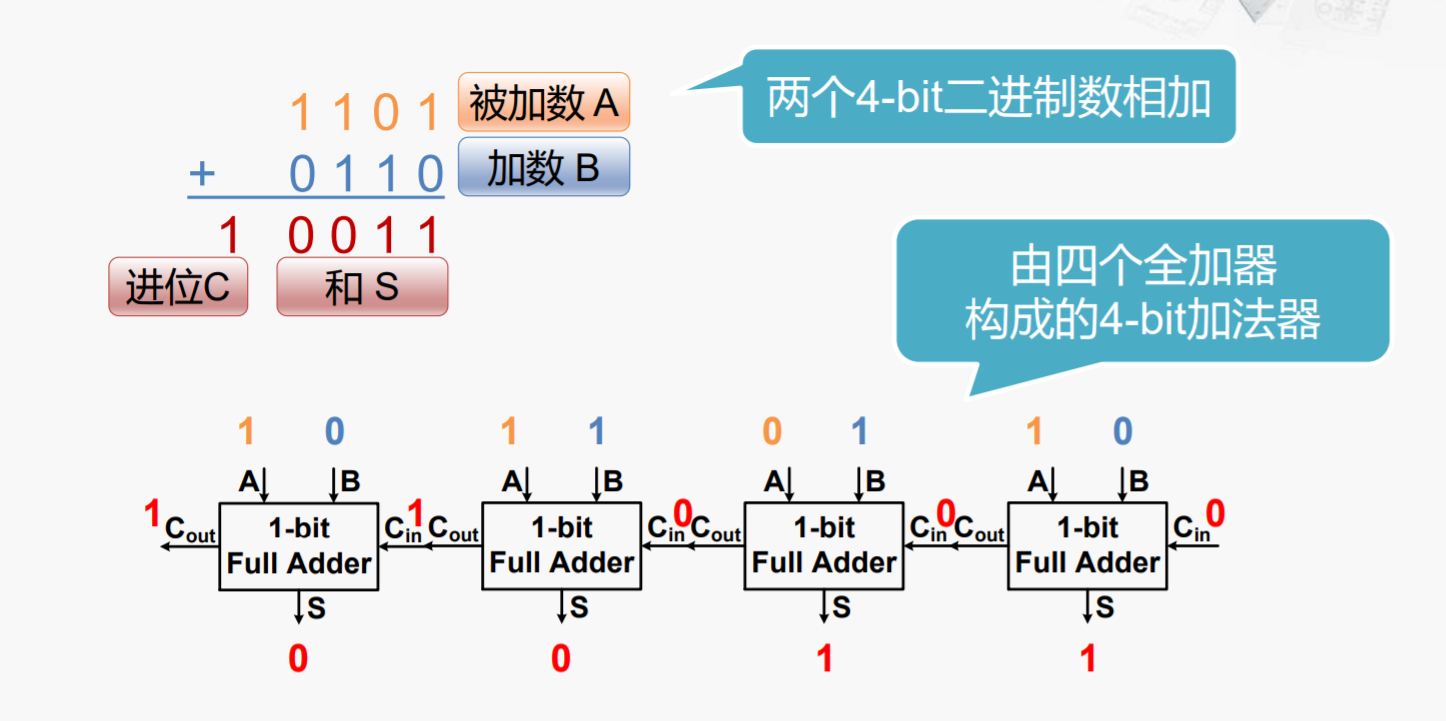
不难发现整个过程是从右至左依次执行,每一个进位需要等前面的运算全完成,可以在一开始得到所有的进位吗?
行波进位加法器(Ripple-Carry Adder,RCA)
像上面4-bit加法器这样实现的加法器被称作行波进位加法器,所有的进位像波浪一样向左推进。
- 结构特点:低位全加器的Cout连接到高一位全加器Cin
- 优点:电路布局简单,设计方便
- 缺点:高位的运算必须等待低位的运算完成
4-bit RCA的门电路实现
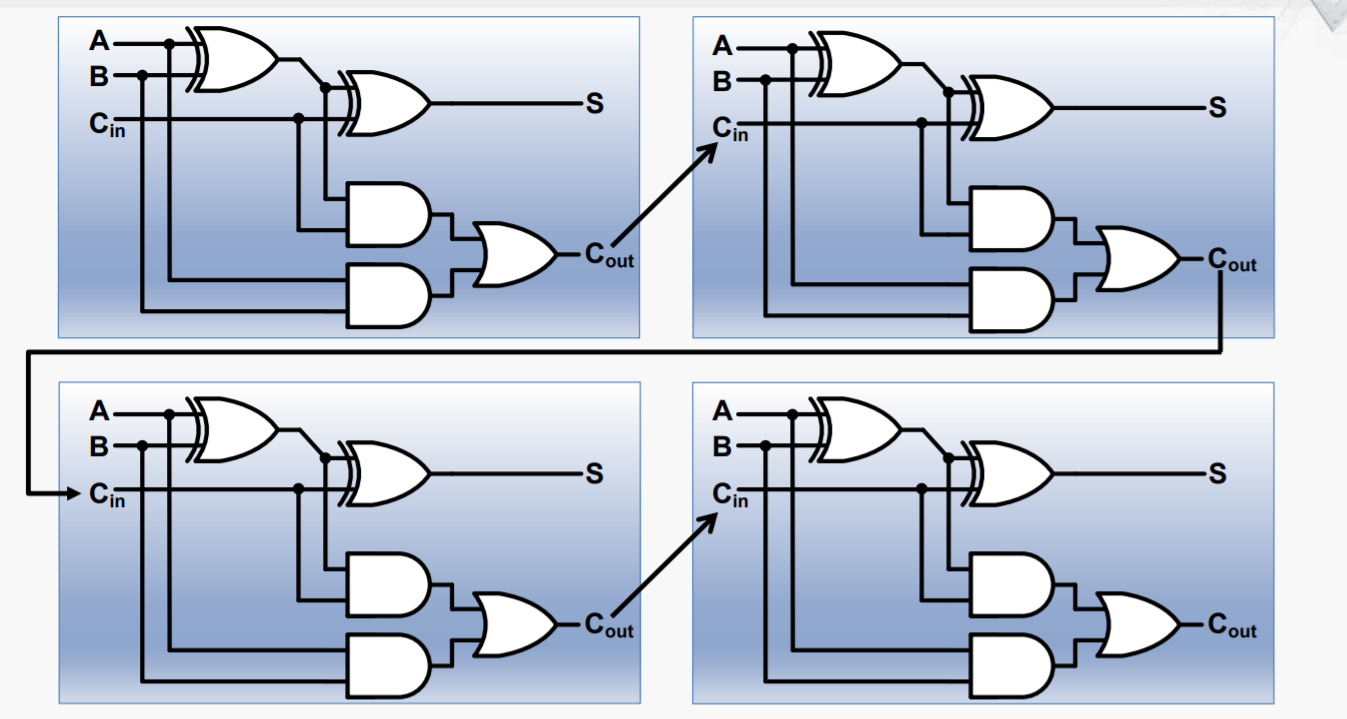
我们考察其中的关键路径(延迟最长的路径)
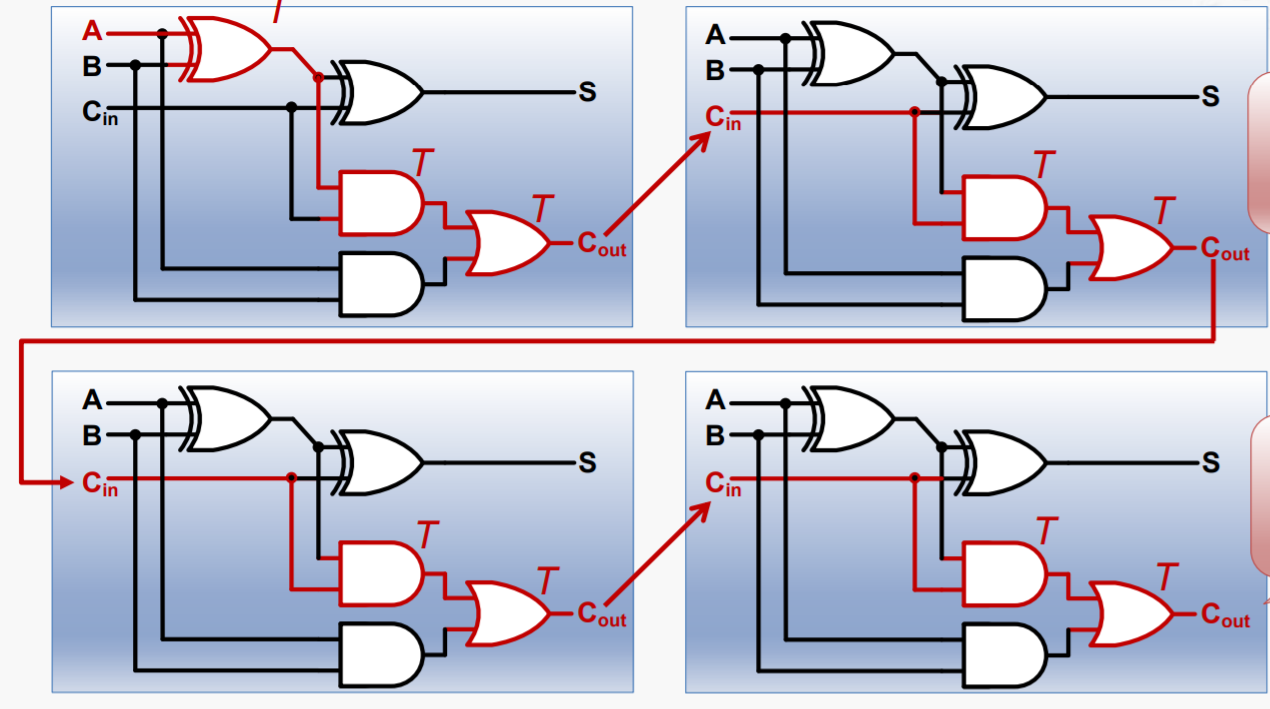
总延迟时间:(T + T)*4 + T = 9T,推广到n位,总时间为(2n + 1)*T。降低总延迟时间就是我们优化的方向。
加法器的优化思路
主要思路:提前计算出“进位信号”。对进位信号进行分析:
$C_{i+1} = (A_i · B_i) + (A_i · C_i) + (B_i · C_i) = (A_i · B_i) + (A_i + B_i) · C_i$
设:生成信号(Genarate):$G_i = A_i · B_i$,传播信号(Propagate):$P_i = A_i + B_i$,则:$C_{i+1} = G_i + P_i · C_i$
如果把这看作一个递推公式,这是一个等差函数,通项可直接求出来,且只与$A_i$和$B_i$有关。这样就可以提前计算出每个“进位信号”,如图:

分析一下电路实现

超前进位加法器(Carry-Lookahead Adder,CLA)
像上面那样通过一个电路提前计算进位的加法器叫做超前进位加法器,具体如图:
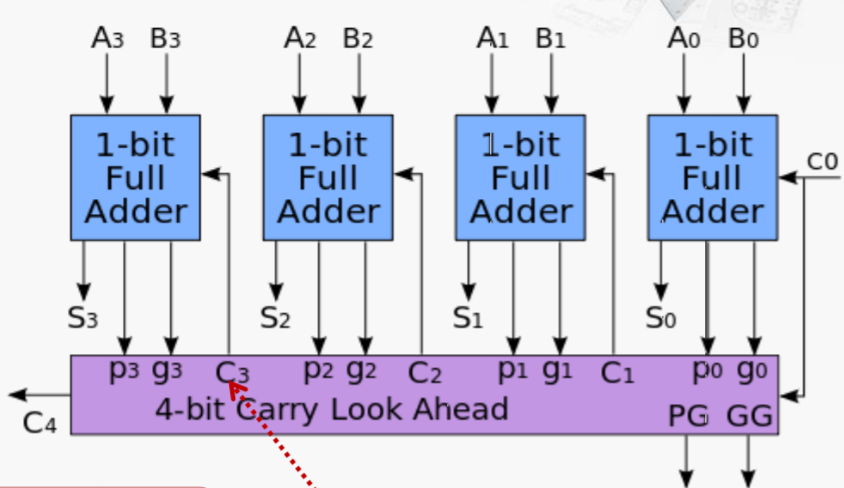
其中,C1、C2、C3、C4都由下面的电路计算好,需要3级门延迟,然后在全加器中关键路径上还有1级延迟,如图
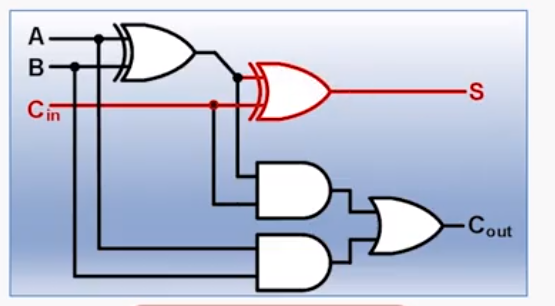
所以,总共有4级门延迟。
- 如果采用这种完全的超前进位,理论上的门延迟都是4级门延迟
- 实际电路过于复杂,难以实现(C31需要32位的与门和或门?hh)
- 通常的方法:采用多个小规模的超前进位加法器拼接而成,例如,用4个8-bit的超前进位加法器连接成32-bit加法器
参考链接:https://www.coursera.org/learn/jisuanji-zucheng/lecture/Y1Q3C/306-jia-fa-qi-de-you-hua
个性签名:时间会解决一切


 浙公网安备 33010602011771号
浙公网安备 33010602011771号