模拟退火
简介
随机这种东西,貌似在ACM里好像就是用于骗分。
但其实有更多实际的用处(用
代替
防止快排退化,用
构建Treap树保持二叉搜索树的平衡等等),还有就是模拟退火算法,也算是随机化算法中一个极好的例子吧。
模拟退火是一种随机化算法,常用于求函数极值。当一个问题的方案数量极大(甚至是无穷的),我们一般有两个选择。
爬山算法
爬山算法每次在当前找到的方案附近寻找一个新的方案(常见方式是随机一个差值), 然后如果这个解更优那么直接转移.
对于单峰函数来说这显然可以直接找到最优解(不过你都知道它是单峰函数了为啥不三分呢?)
但是对于多数我们求解的函数来说, 它并不一定会长成这个样子...于是就极其有可能钻进一个局部的最优解出不来了。
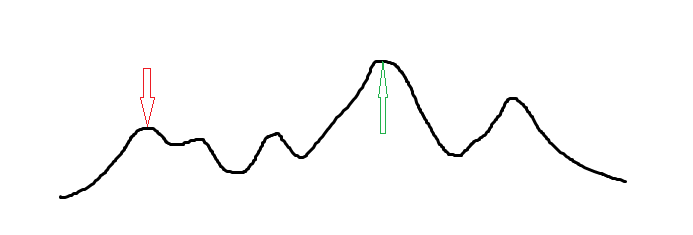
模拟退火
根据爬山算法的过程,我们发现:对于一个当前最优解附近的非最优解,爬山算法直接舍去了这个解。而很多情况下,我们需要去接受这个非最优解从而跳出这个局部最优解,即为模拟退火算法。
退火其实本来是冶金工业里的术语...大概过程是先把晶体加热到极高的温度再缓慢降温, 在这个过程中减少晶体中的缺陷(达到能量最低的最稳定状态)
然后机智的我们发现这个过程最终和我们的最优化过程类似!
模拟退火算法描述
根据热力学规律并结合计算机对离散数据的处理, 我们定义: 当前温度为T,当前状态与新状态之间的差值为ΔE,则发生状态转移的概率为
P(ΔE) = exp(ΔE/T)
显然,如果ΔE为正的话一定会转移成功,但是对于ΔE<0则以上面这个概率接受这个新解
然后我们维护温度T即可,这里我们有三个参数:处温T0,降温系数C,终温Tk.
一般T0是一个较大的数,C是一个接近1但小于1的值,Tk是一个接近0的正数.
首先,让T=T0,然后进行一次转移尝试,T*=C.
当T < Tk时模拟退火过程结束,当前解作为最优解
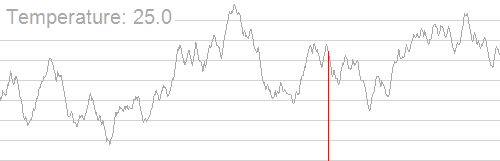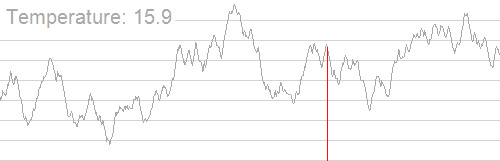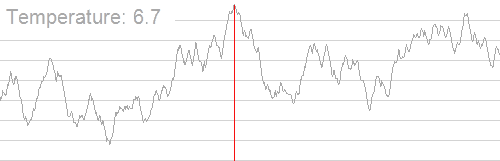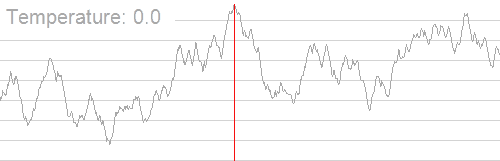
具体过程还是看Wikipedia上的动图吧:
(随着温度的降低,跳跃越来越不随机,最优解也越来越稳定)
模拟退火的实际使用
-
例题
gty又虐了一场比赛,被虐的蒟蒻们决定吊打gty。gty见大势不好机智的分出了n个分身,但还是被人多势众的蒟蒻抓住了。蒟蒻们将n个gty吊在n根绳子上,每根绳子穿过天台的一个洞。这n根绳子有一个公共的绳结x。吊好gty后蒟蒻们发现由于每个gty重力不同,绳结x在移动。蒟蒻wangxz脑洞大开的决定计算出x最后停留处的坐标,由于他太弱了决定向你求助。
不计摩擦,不计能量损失,由于gty足够矮所以不会掉到地上。(详情)
- 思路
问题其实就是找一个点,使得
最小,使用模拟退火算法即可。
为什么这样,(去看链接里的图,文字表诉似乎不是很好理解),因为到达稳定状态要让整个体系的总重力势能最低(总能量最低,没有动能的情况下)。
- 代码
1 #include<cstdio> 2 #include<cmath> 3 using namespace std; 4 5 const double INF = 1e17; 6 const double EPS = 1e-5; //小点好啊,1e-3不让过。。。 7 const double PI = acos(-1.0); 8 const double C = 0.99; //降温系数c 9 const int maxn = 10000 + 10; 10 struct Point 11 { 12 double x, y, w; 13 Point(double _x,double _y):x(_x),y(_y){} 14 Point(){} 15 void Read() { 16 scanf("%lf%lf%lf", &x, &y, &w); 17 } 18 void operator += (Point t) { 19 x += t.x; y += t.y; 20 } 21 void operator /= (int n) { 22 x /= n; y /= n; 23 } 24 }; 25 int n; 26 Point now, ans, points[maxn]; 27 double tmp_min = INF; //当前最小和 28 29 inline double Dist(Point a, Point b) 30 { 31 return sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y)); 32 } 33 inline double Cal(Point p) 34 { 35 double res = 0.0; 36 for (int i = 0; i < n; i++) res += Dist(p, points[i]) * points[i].w; 37 if (res < tmp_min) tmp_min = res, ans = p; 38 return res; 39 } 40 inline double Rand() 41 { 42 return (rand() % 1000 + 1.0) / 1000.0; 43 } 44 45 int main() 46 { 47 srand(19260817); 48 scanf("%d", &n); 49 for (int i = 0; i < n; i++) points[i].Read(), now += points[i]; 50 now /= n; 51 double T = 100000.0, alpha, detal; //T既表示最高温度,也表示最大变化范围,alhpa变化系数,detal表示差值 52 while (T > EPS) 53 { 54 alpha = 2.0 * PI * Rand(); 55 Point tmp(now.x + T * cos(alpha), now.y + T * sin(alpha)); 56 detal = Cal(now) - Cal(tmp); 57 if (detal >= 0 || exp(detal / T) >= Rand()) now = tmp; 58 T *= C; 59 } 60 61 //小范围再次寻找,提高精度 62 T = 0.001; 63 int cnt = 1000; 64 while (cnt--) 65 { 66 alpha = 2.0 * PI * Rand(); 67 Point tmp(ans.x + T * cos(alpha) * Rand(), ans.y + T * sin(alpha) * Rand()); 68 Cal(tmp); 69 } 70 71 printf("%.3lf %.3lf\n",ans.x,ans.y); 72 73 return 0; 74 }
- 注意
1、为什么效率变化会这么快,其实是伪代码中降温率c取值的原因,降温率越慢,速度越慢(但结果越精确),反之速度越快,但就有可能像那个WA一样降温过快,还没找到最优解温度已经趋于了稳定,所以实际应用时不建议这个值设置得过小。
一般降温系数C与1的差减少一个数量级,时间消耗大约多10倍;T0,Tk,变化一个数量级,时间消耗不会变化太大
2、提高精度的小技巧:根据当前温度决定差值的范围. 这样在降温即将结束接近最优解的时候可以有更大的概率更精确地命中最优解.
3、但顺便说一句,BZOJ, ZOJ, POJ都不允许使用time()函数(防止出现漏洞),因此用srand()初始化时应该用一个常数。(经典质数hh)
-
爬山算法
只有发现更优解才更新(没有非最优解跳出的那部分代码)
只需删去那句代码
即将
1 if (detal >= 0 || exp(detal / T) >= Rand()) now = tmp;
替换成
1 if (detal > 0) now = tmp;
洛谷测评前者用时210ms,后者只需182ms
参考链接:
1、https://zhuanlan.zhihu.com/p/21277465
2、https://www.cnblogs.com/rvalue/p/8678318.html
3、https://blog.csdn.net/hydingsy/article/details/81945795
4、https://blog.csdn.net/Icefox_zhx/article/details/80543899
Tk


 浙公网安备 33010602011771号
浙公网安备 33010602011771号