替罪羊树的原理及实例

[Scapegoat Tree] & BZOJ3224

识替罪羊树之算法乃吾生之幸也！

0x00 扯淡

知乎上面有个问题问最优雅的算法是什么，我觉得暴力即是优雅。

当然这里说的暴力并不是指那种不加以思考的无脑的暴力，而是说用繁琐而技巧性的工作可以实现的事，我用看似简单的思想和方法，也可以达到近似于前者的空间复杂度和时间复杂度，甚至可以更优，而其中也或多或少的夹杂着一些"LESS IS MORE"的思想在其中。

以下文章需要对普通二叉搜索树和Treap树（可选）有一定的了解，可以自行百度也可以等我出的一篇有关这个的文章。

0x01 替罪羊树[Scapegoat Tree]

对于一棵二叉搜索树，最重要的事情就是维护他的平衡，以保证对于每次操作（插入，查找，删除）的时间均摊下来都是 $O(logN)$ 乃至 $O(lgN)$ （红黑树，但是常数大而且难写，此处不展开介绍）。

为了维护树的平衡，各种平衡二叉树绞尽脑汁方法五花八门，但几乎都是通过旋转的操作来实现（AVL 树，红黑树，Treap 树（经@GadyPu指正，可持久化Treap树不需要旋转），Splay…），只不过是在判断什么时候应该旋转上有所不同。但替罪羊树就是那么一棵特立独行的猪，哦不，是一只特立独行的树。

0x02 各种嘿嘿嘿的操作

重构

重构允许重构整棵替罪羊树，也允许重构替罪羊树其中的一棵子树。

重构这个操作看似高端，实则十分暴力（真）。主要操作就是把需要重构的子树拍平（由于子树一定是二叉搜索树，所以拍平之后的序列一定也是有序的），然后拎起序列的中点，作为根部，剩下的左半边序列为左子树，右半边序列为右子树，接着递归对左边和右边进行同样的操作，直到最后形成的树中包含的全部为点而不是序列（这样形成的一定是一棵完全二叉搜索树，也是最优的方案）。

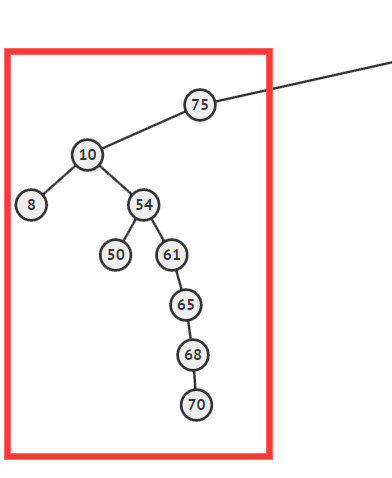
这是一棵需要维护的子树，虽然目前不知道基于什么判断条件，但这棵是明显需要维护的。

$O(n)$ 拍平之后的结果，直接遍历即可。子树的重构就完成了。

插入

插入操作一开始和普通的二叉搜索树无异，但在插入操作结束以后，从插入位置开始一层一层往上回溯的时候，对于每一层都进行一次判断 $h(v) > log(1/\alpha )(size(tree))$ ，一直找到最后一层不满足该条件的层序号（也就是从根开始的第一层不满足该条件的层序号），然后从该层开始重构以该层为根的子树（一个节点导致树的不平衡，就要导致整棵子树被拍扁，估计这也是“替罪羊”这个名字的由来吧）。

每次插入操作的复杂度为 $O(log_{n})$ ，每次重构树的复杂度为 $O(n)$ ，但由于不会每次都要进行重构，也不会每次都重构一整棵树，所以均摊下来的复杂度还是 $O(log_{n})$ 。

$\alpha$ 在这里是一个常数，可以通过调整 $\alpha$ 的大小来控制树的平衡度，使程序具有很好的可控性

------------- $2016/5/30$ 日更新-------------

为了测试 $\alpha$ 值的选取对于程序性能的影响，枚举了 $(0.5,1)$ 这个区间内 $\alpha$ 的值，性能绘制成图标如下（数据采用BZOJ 6,7,8三组数据的3倍）

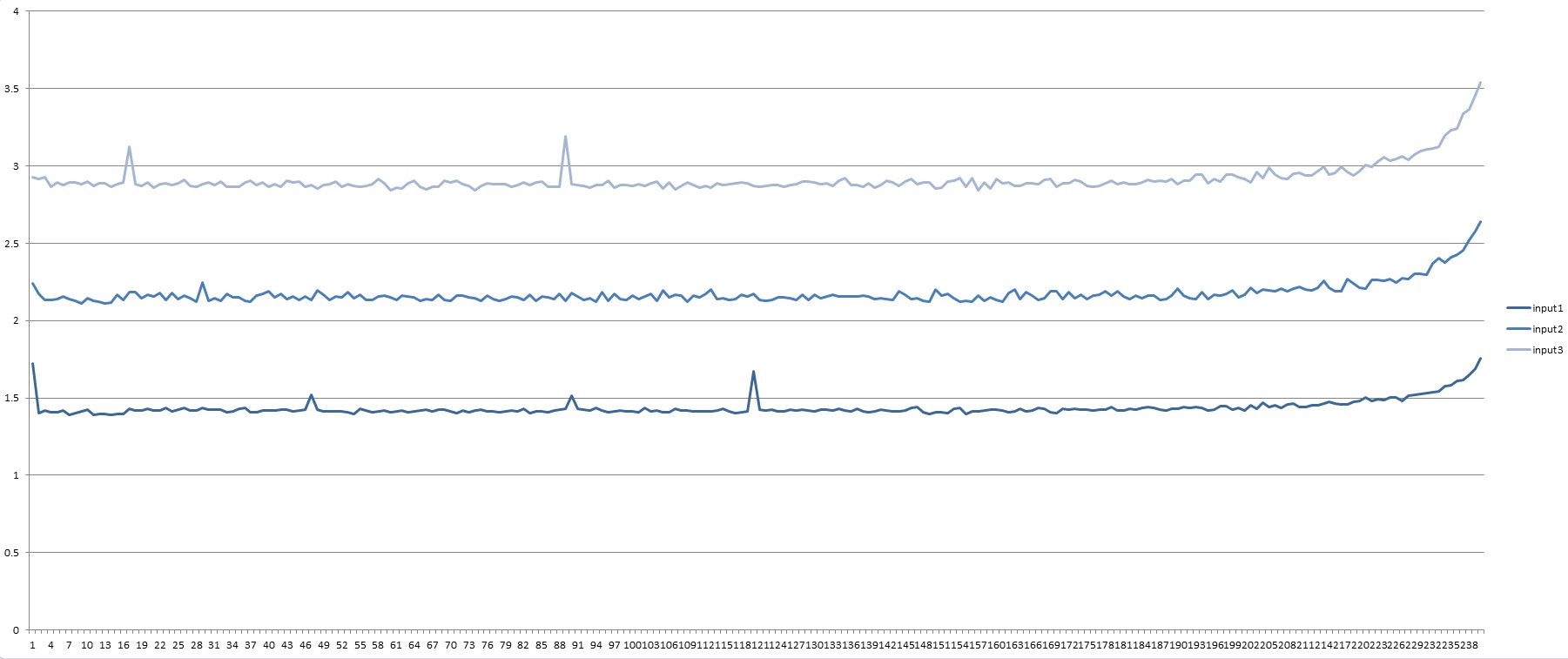
（测试结果如上）

由此可见， $(0.5,1)$ 区间内 $\alpha$ 的取值对于程序性能并没有很大的影响，当然也有可能是我测试方法不当，

------------- $2016/6/1$ 日更新-------------

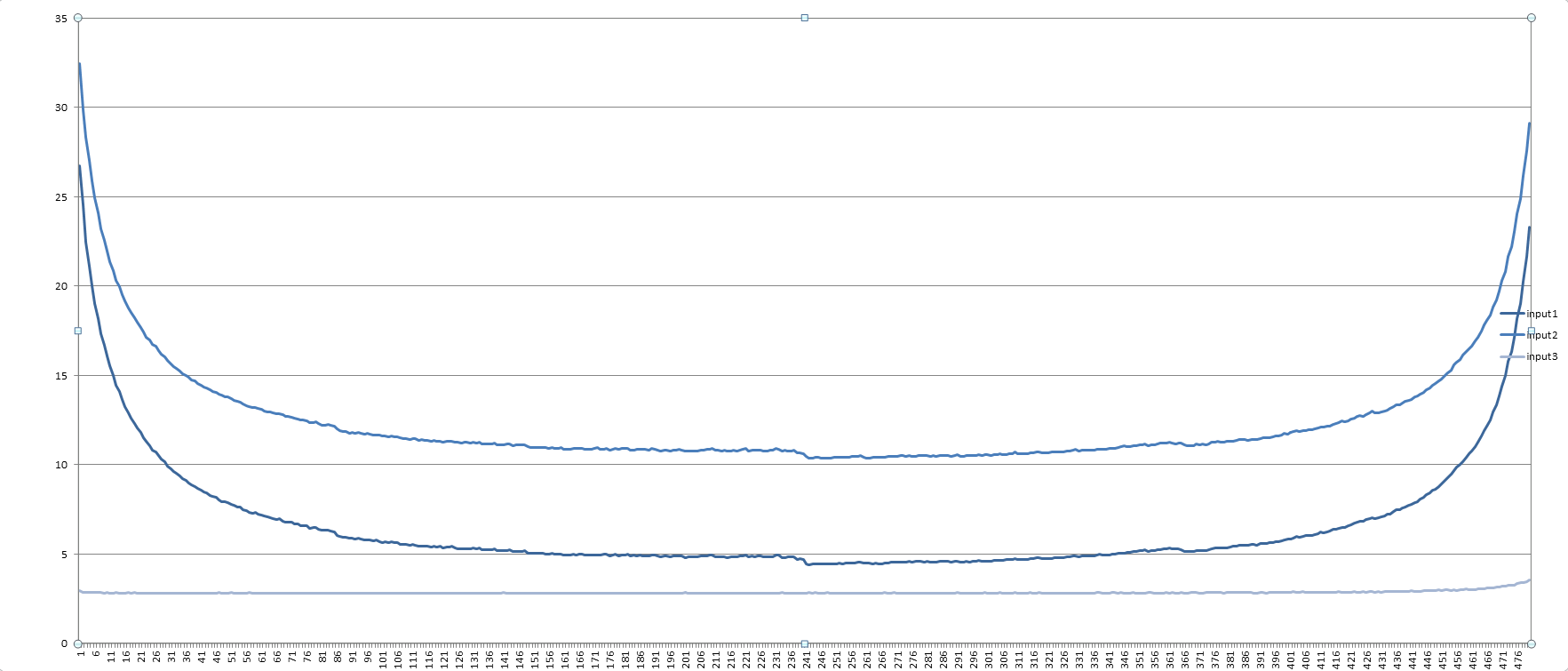
（测试结果如上）

对于取值越靠近两端的确速度越慢，但中间貌似还是没有什么差异。如果有好的数据构造方法希望能提出，一定会再次尝试，谢谢。

删除（惰性删除）

我觉得删除操作是替罪羊树中最好玩的地方，替罪羊树的删除节点并不是真正的删除，而是惰性删除（即给节点增加一个已经删除的标记，删除后的节点与普通节点无异，只是不参与查找操作而已）。当删除的数量超过树的节点数的一半时，直接重构！（屌丝和暴力属性 $MAX$ ），可以证明均摊下来的复杂度还是 $O(log_{n})$ （作者太傻证明不来）。

查找第K大&查找数X的序号

和普通的二叉搜索树无异，但是需要注意标明被删除掉的节点不能被算入。

0x03 代码

以下是替罪羊树的模板，大部分操作直接调用成员函数就可以了。

  1 #include <vector>
  2 using namespace std;
  3 
  4 namespace Scapegoat_Tree {
  5 #define MAXN (100000 + 10)
  6     const double alpha = 0.75;
  7     struct Node {
  8     Node * ch[2];
  9     int key, size, cover; // size为有效节点的数量，cover为节点总数量 
 10     bool exist;    // 是否存在（即是否被删除） 
 11     void PushUp(void) {
 12         size = ch[0]->size + ch[1]->size + (int)exist;
 13         cover = ch[0]->cover + ch[1]->cover + 1;
 14     }
 15     bool isBad(void) { // 判断是否需要重构 
 16         return ((ch[0]->cover > cover * alpha + 5) || 
 17                 (ch[1]->cover > cover * alpha + 5));
 18         }
 19     };
 20     struct STree {
 21     protected:
 22         Node mem_poor[MAXN]; //内存池，直接分配好避免动态分配内存占用时间 
 23         Node *tail, *root, *null; // 用null表示NULL的指针更方便，tail为内存分配指针，root为根 
 24         Node *bc[MAXN]; int bc_top; // 储存被删除的节点的内存地址，分配时可以再利用这些地址 
 25 
 26         Node * NewNode(int key) {
 27             Node * p = bc_top ? bc[--bc_top] : tail++;
 28             p->ch[0] = p->ch[1] = null;
 29             p->size = p->cover = 1; p->exist = true;
 30             p->key = key;
 31             return p;
 32         }
 33         void Travel(Node * p, vector<Node *>&v) {
 34             if (p == null) return;
 35             Travel(p->ch[0], v);
 36             if (p->exist) v.push_back(p); // 构建序列 
 37             else bc[bc_top++] = p; // 回收 
 38             Travel(p->ch[1], v);
 39         }
 40         Node * Divide(vector<Node *>&v, int l, int r) {
 41             if (l >= r) return null;
 42             int mid = (l + r) >> 1;
 43             Node * p = v[mid];
 44             p->ch[0] = Divide(v, l, mid);
 45             p->ch[1] = Divide(v, mid + 1, r);
 46             p->PushUp(); // 自底向上维护，先维护子树 
 47             return p;
 48         }
 49         void Rebuild(Node * &p) {
 50             static vector<Node *>v; v.clear();
 51             Travel(p, v); p = Divide(v, 0, v.size());
 52         }
 53         Node ** Insert(Node *&p, int val) {
 54             if (p == null) {
 55                 p = NewNode(val);
 56                 return &null;
 57             }
 58             else {
 59                 p->size++; p->cover++;
 60                 
 61                 // 返回值储存需要重构的位置，若子树也需要重构，本节点开始也需要重构，以本节点为根重构 
 62                 Node ** res = Insert(p->ch[val >= p->key], val);
 63                 if (p->isBad()) res = &p;
 64                 return res;
 65             }
 66         }
 67         void Erase(Node *p, int id) {
 68             p->size--;
 69             int offset = p->ch[0]->size + p->exist;
 70             if (p->exist && id == offset) {
 71                 p->exist = false;
 72                 return;
 73             }
 74             else {
 75                 if (id <= offset) Erase(p->ch[0], id);
 76                 else Erase(p->ch[1], id - offset);
 77             }
 78         }
 79     public:
 80         void Init(void) {
 81             tail = mem_poor;
 82             null = tail++;
 83             null->ch[0] = null->ch[1] = null;
 84             null->cover = null->size = null->key = 0;
 85             root = null; bc_top = 0;
 86         }
 87         STree(void) { Init(); }
 88 
 89         void Insert(int val) {
 90             Node ** p = Insert(root, val);
 91             if (*p != null) Rebuild(*p);
 92         }
 93         int Rank(int val) {
 94             Node * now = root;
 95             int ans = 1;
 96             while (now != null) { // 非递归求排名 
 97                 if (now->key >= val) now = now->ch[0];
 98                 else {
 99                     ans += now->ch[0]->size + now->exist;
100                     now = now->ch[1];
101                 }
102             }
103             return ans;
104         }
105         int Kth(int k) {
106             Node * now = root;
107             while (now != null) { // 非递归求第K大 
108                 if (now->ch[0]->size + 1 == k && now->exist) return now->key;
109                 else if (now->ch[0]->size >= k) now = now->ch[0];
110                 else k -= now->ch[0]->size + now->exist, now = now->ch[1];
111             }
112         }
113         void Erase(int k) {
114             Erase(root, Rank(k));
115             if (root->size < alpha * root->cover) Rebuild(root);
116         }
117         void Erase_kth(int k) {
118             Erase(root, k);
119             if (root->size < alpha * root->cover) Rebuild(root);
120         }
121     };
122 #undef MAXN
123 
124 }

小小的封装了一下。

如果对封装不习惯的，这里有一个为封装的：https://www.luogu.org/record/show?rid=14045715

0x04 例题

来看一道例题：P3369

您需要写一种数据结构（可参考题目标题），来维护一些数，其中需要提供以下操作：

插入x数2. 删除x数(若有多个相同的数，因只删除一个)
查询x数的排名(若有多个相同的数，因输出最小的排名)
查询排名为x的数
求x的前驱(前驱定义为小于x，且最大的数)
求x的后继(后继定义为大于x，且最小的数)

Input

第一行为 $n\leq 100000$ ，表示操作的个数,下面n行每行有两个数 $opt$ 和 $x$ ， $opt$ 表示操作的序号( $1\leq opt\leq 6$ )。

Output

对于操作 $\left\{ 3,4,5,6 \right\}$ 每行输出一个数，表示对应答案。

Sample Input

Sample Output

106465
84185
492737

0x05 题解

模板题，套用上面的就可以了。

 1 /**************************************************************
 2     Problem: 3224
 3     User: SillyVector
 4     Language: C++
 5     Result: Accepted
 6     Time:200 ms
 7     Memory:4112 kb
 8 ****************************************************************/
 9  
10 #include <iostream>
11 #include <cstdio>
12 #include <cstring>
13 #include <vector>
14 using namespace std;
15 
16 /*
17     Template
18 */
19  
20 #define INLINE __attribute__((optimize("O3"))) inline
21 INLINE char NC(void)
22 {
23         static char buf[100000], *p1 = buf, *p2 = buf;
24         if (p1 == p2) {
25                 p2 = (p1 = buf) + fread(buf, 1, 100000, stdin);
26                 if (p1 == p2) return EOF;
27         }
28         return *p1++;
29 }
30 INLINE void read(int &x) {
31         static char c; c = NC(); int b = 1;
32         for (x = 0; !(c >= '0' && c <= '9'); c = NC()) if(c == '-') b = -b;
33         for (; c >= '0' && c <= '9'; x = x * 10 + c - '0', c = NC()); x *= b;
34 }
35 using namespace Scapegoat_Tree;
36  
37 STree _t;
38 int n, k, m;
39 int main(void) {
40         //freopen("in.txt", "r", stdin);
41         //freopen("out.txt", "w", stdout);
42         read(n);
43         while (n--) {
44                 read(k), read(m);
45                 switch (k) {
46                 case 1: _t.Insert(m); break;
47                 case 2: _t.Erase(m); break;
48                 case 3: printf("%d\n", _t.Rank(m)); break;
49                 case 4: printf("%d\n", _t.Kth(m)); break;
50                 case 5: printf("%d\n", _t.Kth(_t.Rank(m) - 1)); break;
51                 case 6: printf("%d\n", _t.Kth(_t.Rank(m + 1))); break;
52                 }
53                 /* DEBUG INFO
54                 vector<Node *> xx;
55                 _t.Travel(_t.root, xx);
56                 cout << "::";
57                 for(int i = 0; i < xx.size(); i++) cout << xx[i]->key << ' '; cout << endl;
58                 */
59         }
60         return 0;
61 
62 }

$200ms$ ，速度我已经很满意了。

再放一道POJ例题：1442 -- Black Box 有兴趣可以试试。

转载于：https://zhuanlan.zhihu.com/p/21263304

posted @ 2018-11-23 11:21 Rogn 阅读(2149) 评论(0) 编辑收藏举报

刷新页面返回顶部

Rogn