DS博客作业05--查找
2021-06-14 20:19 米奈希尔。 阅读(99) 评论(1) 收藏 举报| 这个作业属于哪个班级 | 数据结构--网络2011/2012 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业05--查找 |
| 这个作业的目标 | 学习查找的相关结构 |
|姓名 | 罗发槺 |
0.PTA得分截图

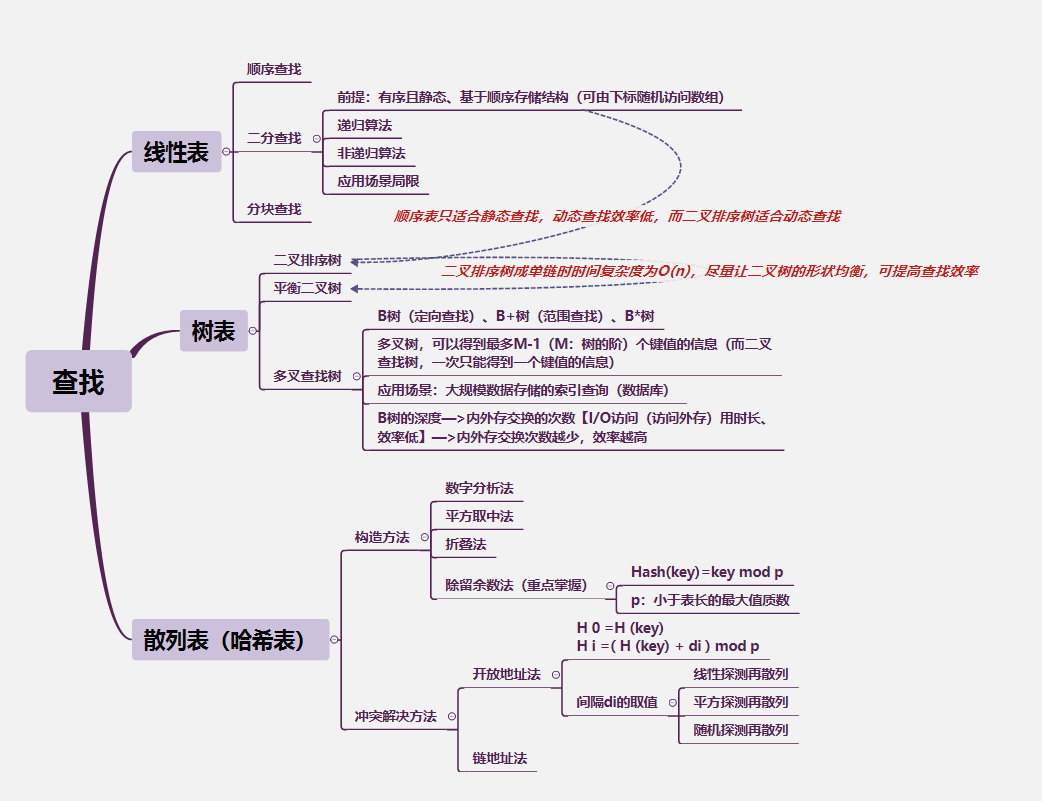
1.本周学习总结(0-5分)
1.啊啊
1.1 查找的性能指标
1.啊啊
ASL成功、不成功,比较次数,移动次数、时间复杂度
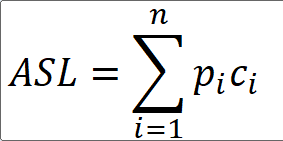
- ASL是衡量查找算法性能好坏的重要指标。一个查找算法的ASL越大,其时间性能越差;反之,一个查找算法的ASL越小,其时间性能越好。
- ASL成功:表示成功查找到查找表中的元素,平均需要关键字比较次数
- ASL不成功:表示没有找到查找表中的元素,平均需要关键字比较次数
- 计较次数:就是查找一个元素在表中的位置,直到确认成功或失败结果这一过程的比较元素个数
- 移动次数:就是处理冲突时放置一个元素直到位置唯一的移动次数
1.2 静态查找
分析静态查找几种算法包括:顺序查找、二分查找的成功ASL和不成功ASL。
1.21顺序查找
即从左往右顺着查找关键字,成功返回元素序号+1,失败返回0.
int SeqSearch(SeqList R,int n,KeyType k)
{
int i=0;
while (i<n && R[i].key!=k)//从表头往后找
i++;
if (i>=n)//未找到返回0
return 0;
else
return i+1;//找到返回逻辑序号i+1
}
若k在表中,顺序查找方法查找成功的平均比较次数约为表长的一半:
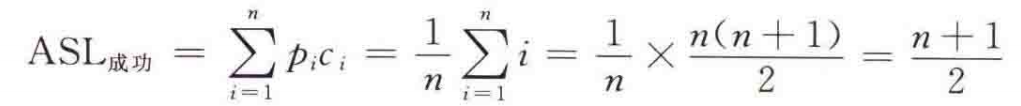
- 若k值不在表中,则必须进行n次比较之后才能确定查找失败

1.21二分查找
折半查找又称二分查找,是一种效率较高的查找方法。但是,折半查找要求线性表是有序表,即表中的元素按关键字有序。
- 基本思路
- 设R[low...high]是当前的查找区间,首先确定该区间的中点位置mid=⌊(low+ high)/2⌋, 然后将待查的k值与R[mid].key比较:
- (1)若k=R[mid].key,则查找成功并返回该元素的逻辑序号。
- (2)若k<R[mid].key,则由表的有序性可知R[mid...high].key均大于k,因此若表中存在关键字等于k的元素,则该元素必定是在位置mid左边的子表R[low...mid-1]中,故新的查找区间是左子表R[low...mid-1]。
- (3)若k> R[mid].key,则关键字为k的元素必在mid的右子表R[mid+ 1...high]中,即新的查找区间是右子表R[mid+1...high]。下一次查找是针对新的查找区间进行的。
int BinSearch(RecType R[],int n,KeyType k)
{
int low=0,high=n-1,mid;
while (low<=high)//当前区间存在元素时循环
{
mid=(low+high)/2;
if (R[mid].key==k)//查找成功返回其逻辑序号mid+1
return mid+1;
if (k<R[mid].key)//继续在R[low...mid-1]中查找
high=mid-1;
else
low=mid+1;//继续在R[mid+1...high]中查找
}
return 0;//未找到时返回0(查找失败)
}
查找成功:
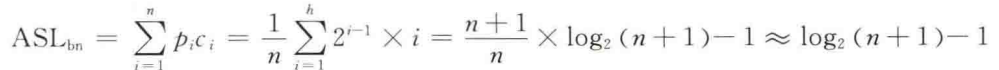
查找失败:
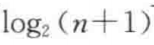
1.3 二叉搜索树
1.3.1 如何构建二叉搜索树(操作)
结合一组数据介绍构建过程,及二叉搜索树的ASL成功和不成功的计算方法。
已数据(5,2,1,6,7,4,8,3,9)为例
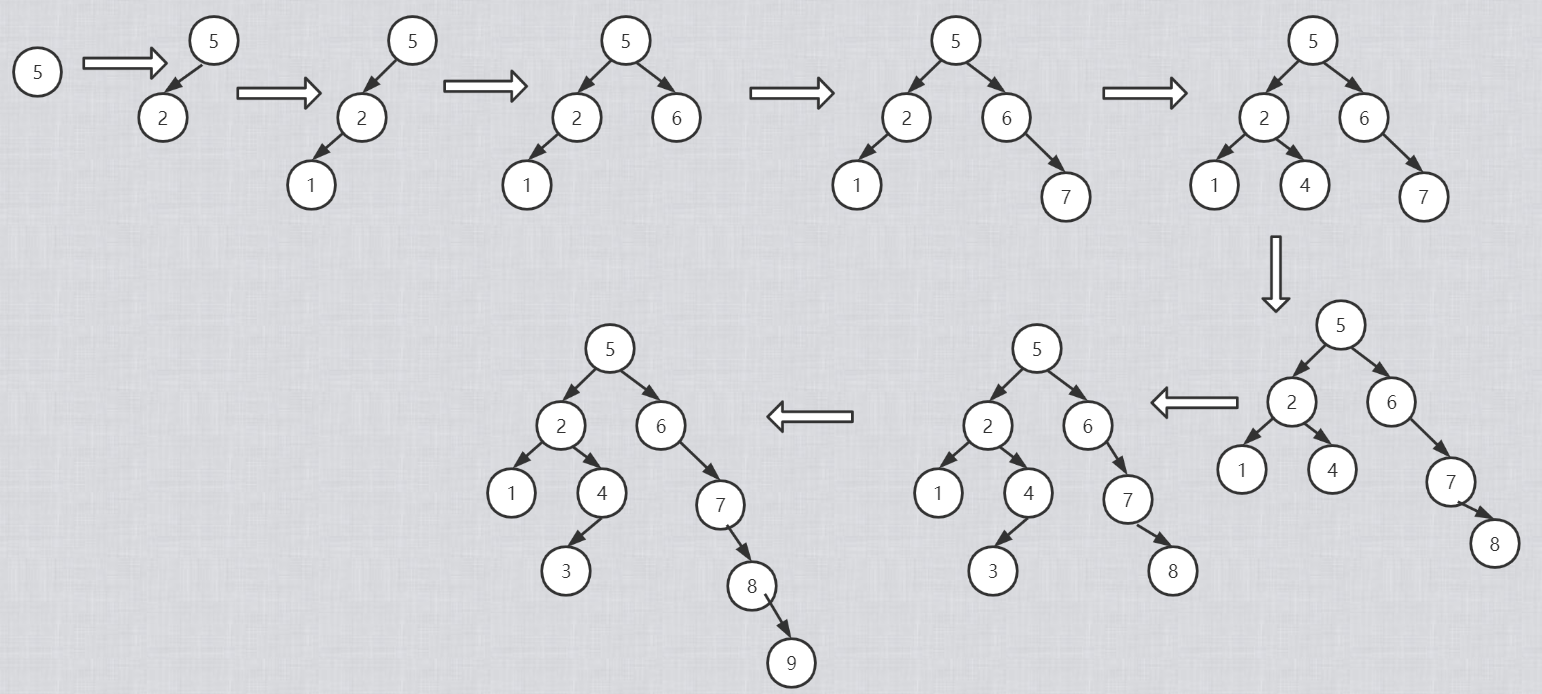
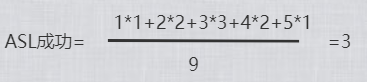
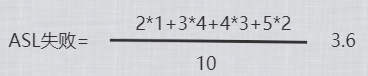
如何在二叉搜索树做插入、删除。
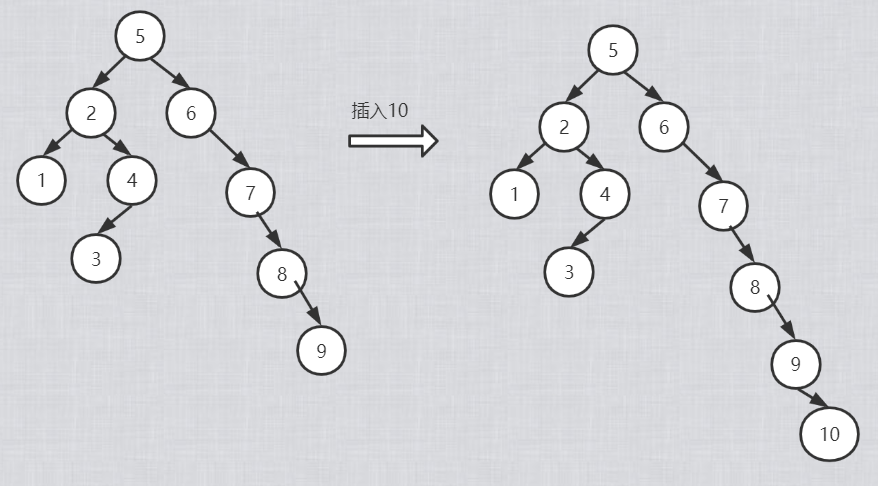
- 删除
分为如下情况:
1)被删除的节点是叶子节点。
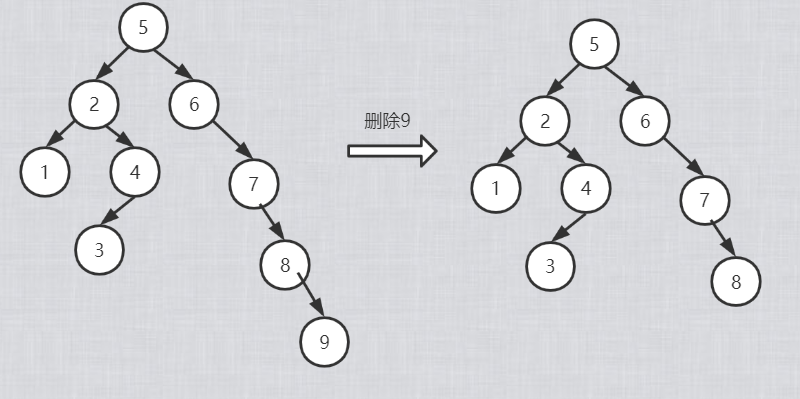
2)被删除的节点只有左子树或者只有右子树,用其左子树或者右子树代替它
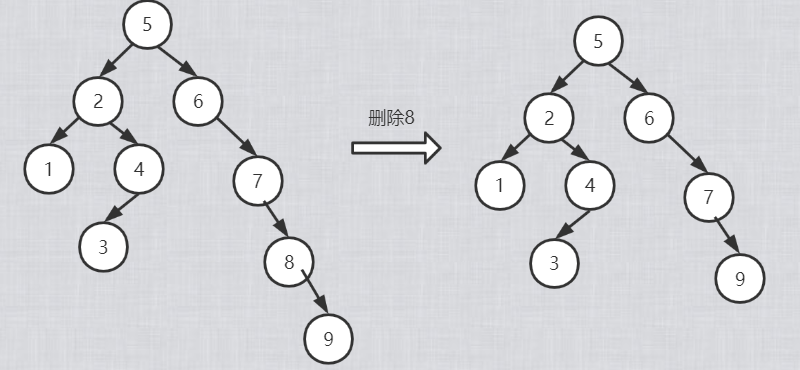
3)被删除的节点既有左子树,也有右子树,可以从其左子树中选最大的结点代替它,或者时从右子树中选最小的结点代替它
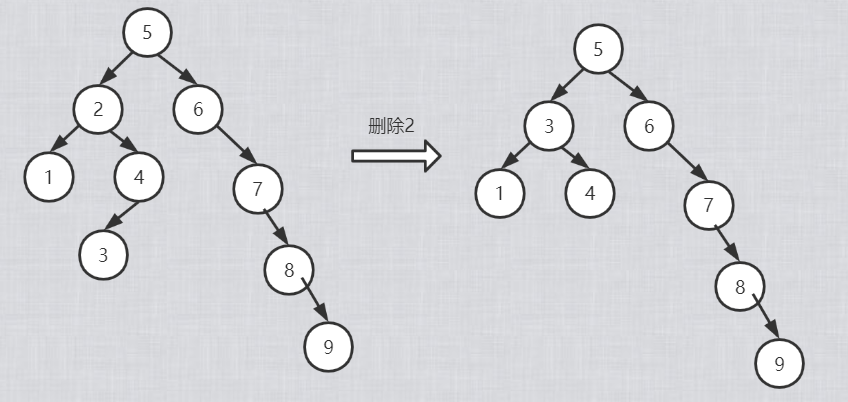
1.3.2 如何构建二叉搜索树(代码)
1.如何构建、插入、删除及代码。
构建代码:
BSTree CreatBST(KeyType a[],int n)//返回树根指针
{
BSTree bt=NULL;//初始时bt为空树
int i=0;
while (i<n)
{
InsertBST(bt,a[i]);//将a[i]插入二叉排序树T中
i++;
}
return bt;//返回建立的二叉排序树的根指针
}
在二叉排序树中插入一个关键字为k的结点要保证插入后仍满足BST性质。其插入过程是:若二叉排序树bt为空,则创建一个key域为
k的结点,将它作为根结点﹔否则将k和根结点的关键字比较,若两者相等﹐则说明树中已有此关键字k ,无须插人,直接返回假;
若k
int InsertBST(BSTree &p,KeyType k)
{
if (p==NULL)//原树为空
{
p=new BSTNode;
p->key=k;
p->lchild=p->rchild=NULL;
return 1;
}
else if (k==p->key) //相同关键字的节点0
return 0;
else if (k<p->key)
return InsertBST(p->lchild,k);//插入到左子树
else
return InsertBST(p->rchild,k);//插入到右子树
}
删除代码:
BinTree Delete( BinTree BST, ElementType X )
{
Position temp;
if(!BST) //如果最终树为空,说明没有
printf("Not Found\n");
else
{
if(X < BST->Data) //从左子树递归删除
BST->Left = Delete(BST->Left,X);
else if(X > BST->Data) //从右子树递归删除
BST->Right = Delete(BST->Right,X);
else //如果当前BST就是要删除的节点
{
if(BST->Left && BST->Right) //要被删除的节点有左右两个孩子,就从右子树中找最小的数替换删除的节点
{
temp = FindMin(BST->Right); //找最小
BST->Data = temp->Data; //替换删除的节点
BST->Right = Delete(BST->Right,temp->Data);//删除拿来替换的那个节点
}
else
{
temp = BST;
if(!BST->Left) //只有右节点
BST = BST->Right; //直接赋值就可以
else if(!BST->Right) //只有左节点
BST = BST->Left; //直接赋值就可以
free(temp);
}
}
}
return BST; //返回删除后的二叉树
}
2.分析代码的时间复杂度
如果二叉排序树是平衡的,则n个节点的二叉排序树的高度为,其查找效率为,近似于折半查找。如果二叉排序树完全不
平衡,则其深度可达到n,查找效率为O(n),退化为顺序查找。一般的,二叉排序树的查找性能在到O(n)之间。因此,
为了获得较好的查找性能,就要构造一棵平衡的二叉排序树。
3.为什么要用递归实现插入、删除?递归优势体现在代码哪里?
时间复杂度低,便于保留父子关系,删除和插入,找到父亲和孩子节点。
1.4 AVL树
- AVL树的特点是:“AVL树中任何结点的两个子树的高度最大差别为1”
1.41 AVL树的4种调整做法。
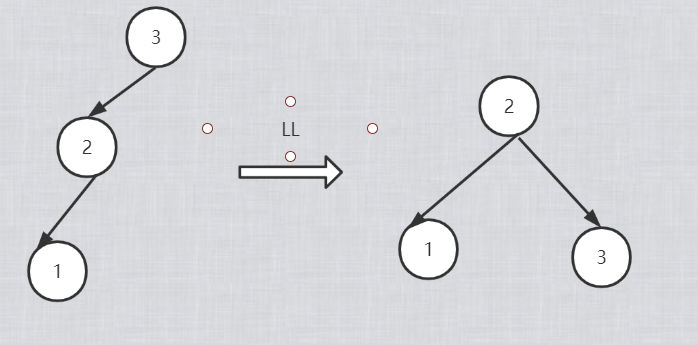
LL型
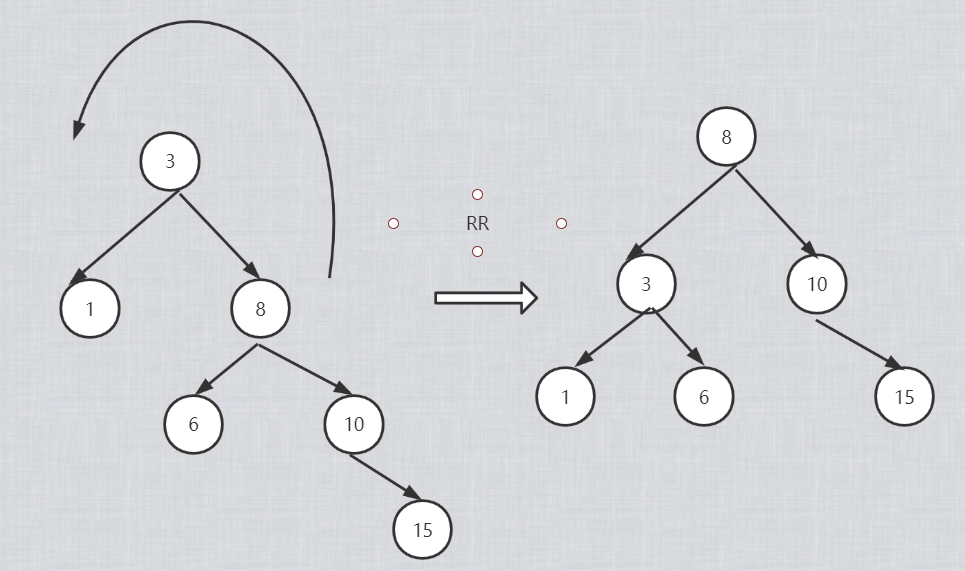
RR型
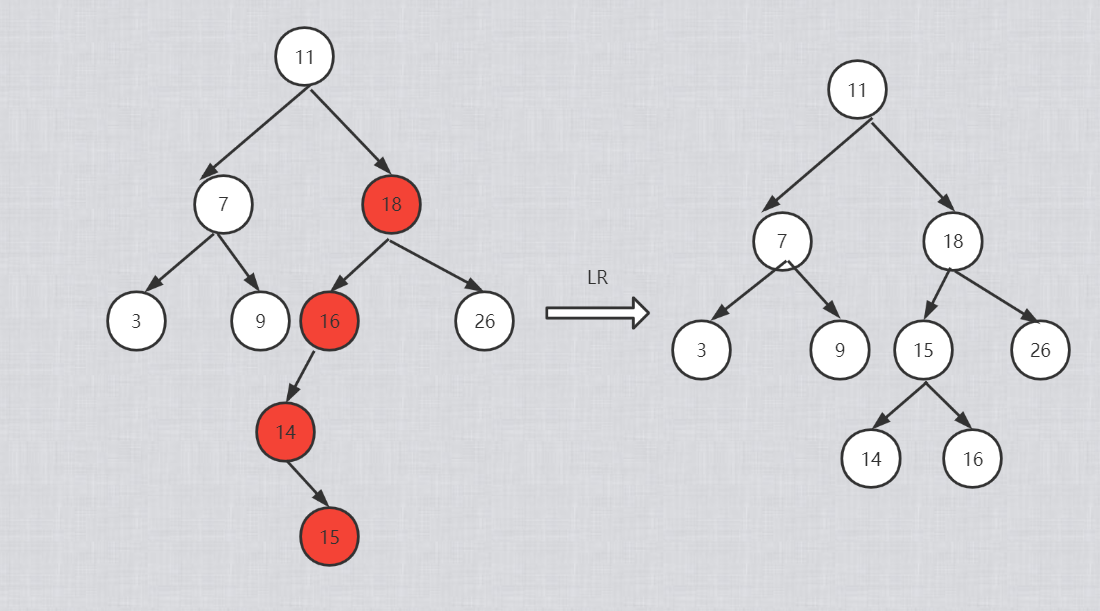
LR型
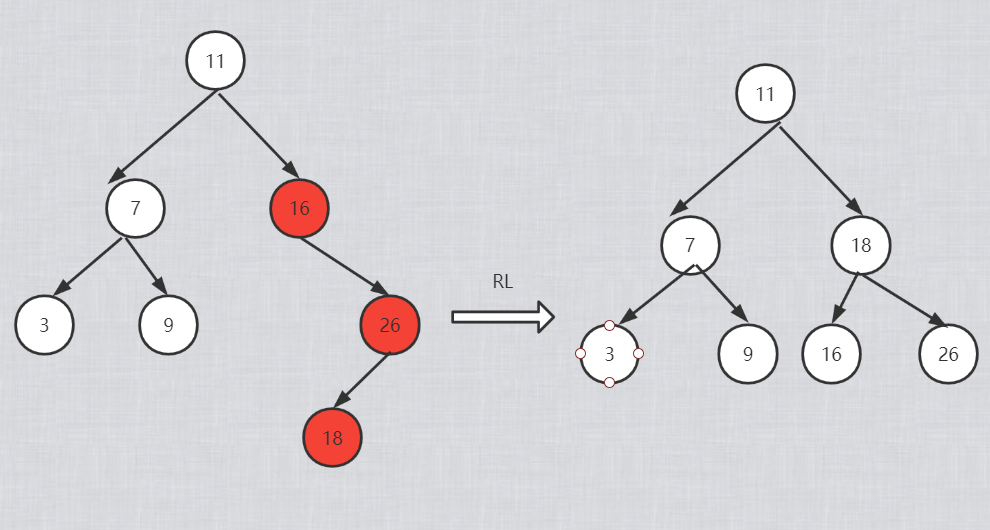
RL型
1.42 AVL树的高度和树的总节点数n的关系?
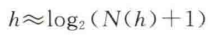
1.43 STL容器map的特点、用法。
-
map映射容器的元素数据是由一个键值和一个映射数据组成的,键值与映照数据之间具有一一映照的关系。
map容器的数据结构也采用红黑树来实现的,插入元素的键值不允许重复,比较函数只对元素的键值进行 -
头文件
#include<map> -
基本操作
begin() 返回指向 map 头部的迭代器
clear() 删除所有元素
count() 返回指定元素出现的次数
empty() 如果 map 为空则返回 true
end() 返回指向 map 末尾的迭代器
erase() 删除一个元素
find() 查找一个元素
insert() 插入元素
key_comp() 返回比较元素 key 的函数
lower_bound() 返回键值>=给定元素的第一个位置
max_size() 返回可以容纳的最大元素个数
rbegin() 返回一个指向 map 尾部的逆向迭代器
rend() 返回一个指向 map 头部的逆向迭代器
size() 返回 map 中元素的个数
swap() 交换两个 map
upper_bound() 返回键值>给定元素的第一个位置
value_comp() 返回比较元素 value 的函数
- 定义一个map容器
map<int,char>mp;//定义map容器 - 插入
普通插入
mp[1]='a'; mp[1]='b';//key不允许重复,再次插入相当于修改value的值 mp[2]='a'; mp[3]='b'; mp[4]='c'; - insert插入
mp.insert(map<int,char>::value_type(5,'d')); - 删除
mp.erase('b');//通过关键字key删除元素
1.5 B-树和B+树
B-树和AVL树区别,其要解决什么问题?
B-树定义。结合数据介绍B-树的插入、删除的操作,尤其是节点的合并、分裂的情况
1.51 B-树结构体定义
#define MAXM 10 //定义B-树的最大的阶数
typedef int KeyType; //KeyType为关键字类型
typedef struct node //B-树节点类型定义
{
int keynum; //节点当前拥有的关键字的个数
KeyType key[MAXM]; //[1..keynum]存放关键字,[0]不用
struct node* parent; //双亲节点指针
struct node* ptr[MAXM];//孩子节点指针数组[0..keynum]
} BTNode;
1.52 B-树的定义:
- 每个节点最多有m-1个关键字(可以存有的键值对)。
- 根节点最少可以只有1个关键字。
- 非根节点至少有m/2个关键字。
- 每个节点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
- 所有叶子节点都位于同一层,或者说根节点到每个叶子节点的长度都相同。
- 每个节点都存有索引和数据,也就是对应的key和value。
1.53B-树的插入
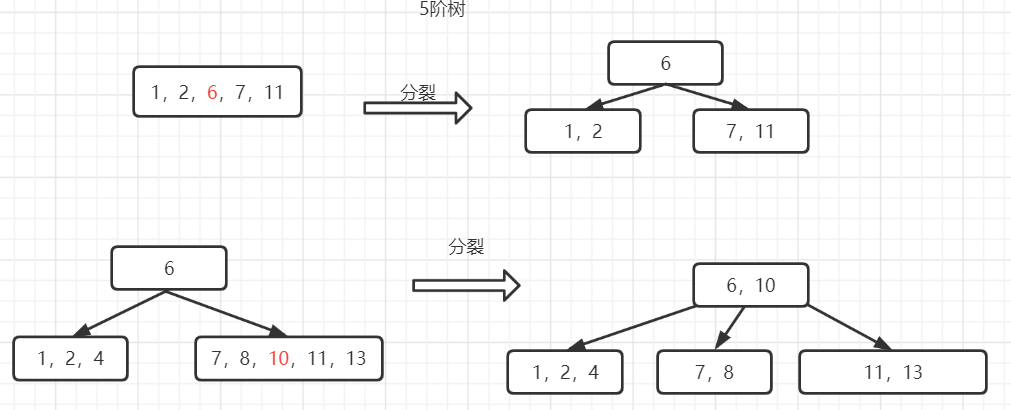
- 向一棵m阶B-树中插入关键字,插入的位置一定在叶子节点层,有两种情况:
- 1.该叶子节点的关键字个数n<m-1,不修改指针,直接插入关键字到此节点中;
- 2.该叶子节点的关键字个数n=m-1,则需进行“节点分裂”,此时若该叶子节点没有双亲节点,则新建一个双亲节点,树的高度增加一层,且双
亲节点的值为叶子节点插入关键字k后的中间位置关键字。若该叶子节点有双亲节点,则将待插入的关键字k插入到双亲节点中
1.54 B-树的删除
删除关键字k分两种情况:
-
1.在叶子节点层上删除关键字k;
-
2.在非叶子节点层上删除关键字k。对于一棵m阶B-树,非根、非叶子节点的关键字最少个数Min为 m/2取上限再减一
-
B-树非叶子节点删除:
- 1.从此节点的子树节点中借调最大或最小关键字代替要删除的关键字;
- 2.子树中删除借调的关键字;
- 3.若子树节点关键字个数小于最小值,重复步骤1;
- 4.若删除关键字在叶子节点层,按叶子节点删除操作法
-
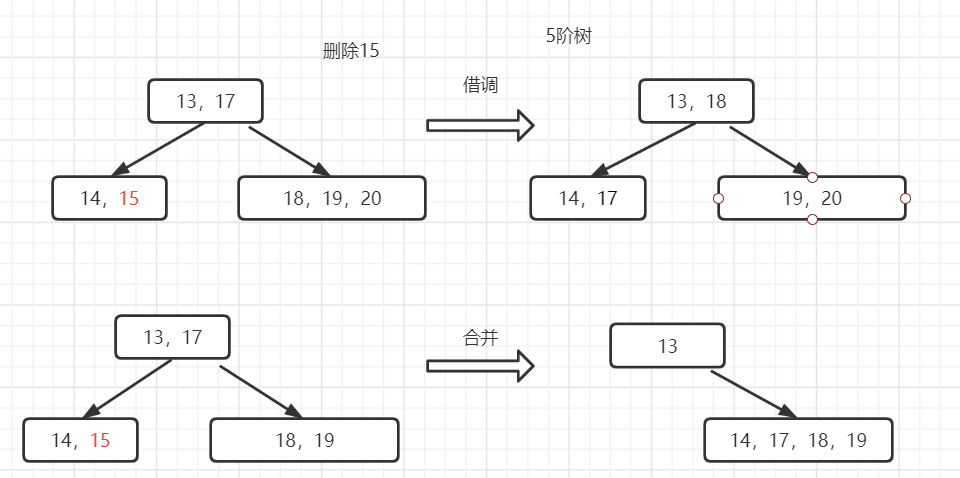
B-树叶子节点删除:B-树的叶子节点b上删除关键字有如下三种情况:
- 1.若b节点的关键字个数大于Min,则可直接删去该关键字;
- 2.若b节点的关键字个数等于Min,且其兄弟节点的关键字个数大于Min,则可以从兄弟节点借。此时兄弟节
点最小关键字上移双亲节点,而双亲节点中大于删除关键字的关键字下移删除节点; - 3.若b节点的关键字个数等于Min,且其兄弟节点的关键字个数等于Min。此时先删除关键字,兄弟节点及删
除关键字节点、双亲节点中分割两者的关键字再合并为一个新叶子节点,若双亲节点关键字个数小于Min,重复上一合并节点的步骤
1.55 B+树定义
- B+树是大型索引文件的标准组织方式,支持顺序查找和分块索引,一棵 m阶B+树满足以下六个条件
- 1.每个分支节点最多有m棵子树
- 2.根节点或者没有子树,或者至少有两棵子树
- 3.除根节点外,其他每个分支节点的子树棵数至少为m/2取上限
- 4.有n棵子树的节点有n个关键字
- 5.所有叶子节点包含全部关键字及指向相应记录的指针,叶子节点按关键字大小顺序链接,叶子节点是直接指向数据文件中的记录
- 6.所有分支节点包含子节点最大关键字及指向子节点的指针
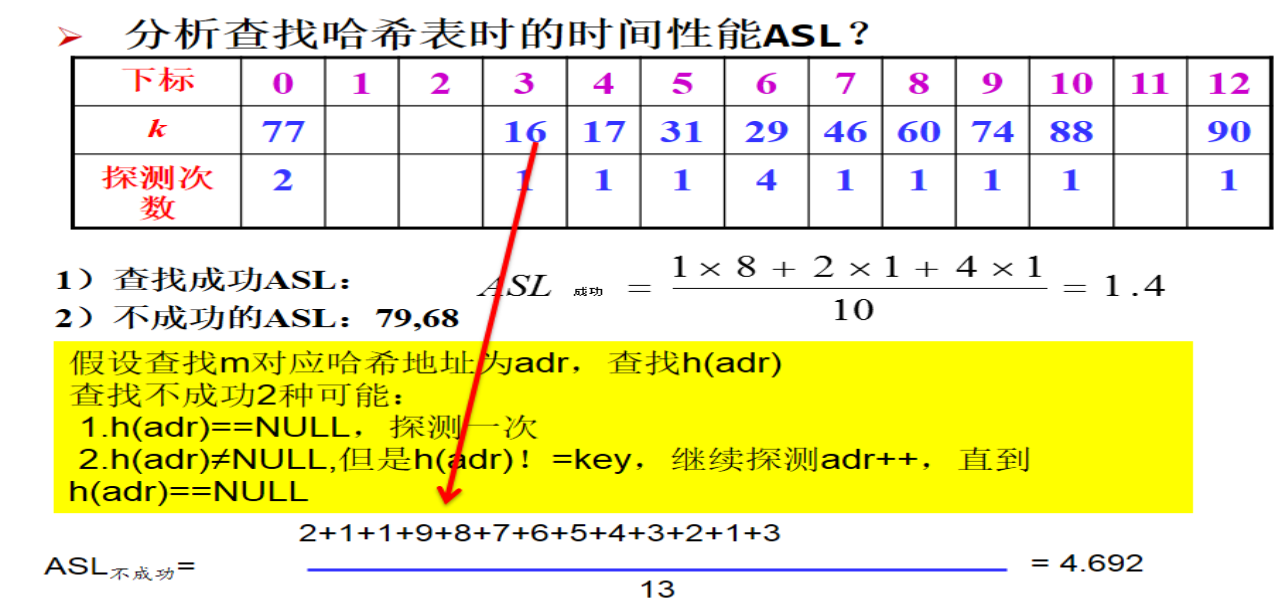
1.6 散列查找。
-
根据设定的哈希函数 H(key)和所选中的处理冲突的方法,将一组关键字映射到一个有限的、地址连续的地址集 (区间) 上,并以关键
字在地址集中的“映像”作为相应记录在表中的存储位置,如此构造所得的查找表称之为“哈希表”。 -
哈希函数h(key):把关键字为k,的对象存放在相应的哈希地址中
-
哈希表:存储数据记录的长度为m (m多n)的连续内存单元
-
构造哈希函数的方法
- 1直接定址法:直接定址法是以关键字k本身或关键字加上某个数值常量c作为哈希地址的方法。直接定址法的哈希函数h(k)为:h(k)=k+c。这种方法是不会出现哈希冲突的,但是,对于数据的格式要求太大了,不适用于所有的情况,并且,如果数据分布不连续的话,会造成内春单元的浪费。这实际上是解决方法上面的差异。
- 除留余数法:除留余数法是用关键字k除以某个不大于哈希表长度m的数p所得的余数作为哈希地址的方法。哈希函数h(k)为:h(k)=k mod p (mod为求余运算,p≤m)这里的p最好是接近于哈希表长度的素数,这样会更大程度上减少哈希冲突的概率。 这是我们最常见的方法。
-
哈希冲突
对于两个关键字分别为ki ,和kj,( i≠j)的记录有ki,≠kj,,但h(ki)=h(kj)。把这种现象叫做哈希冲突(同义词冲突)
哈希表设计主要需要解决哈希冲突。实际中哈希冲突是难以辟免的,主要与3个因素有关:
- 1.哈希表长度
- 与装填因子有关。
- 装填因子α=存储的记录个数/哈希表的大小=n/m
- α越小,冲突可能性就越小;α越大(最大可取1),冲突的可能性就越大。控制在0.6~0.9的范围内
- 2.与所采用的哈希函数有关。
- 3.与解决冲突方法有关。
解决冲突的方法
- 开放定址法:冲突时寻找新的空闲哈希地址。
-
线性探测法:线性探查法的数学递推描述公式为: d0=h(k) di=(di-1+1) mod m (1≤i≤m-1)。遇见冲突将元素向后移动一个位置看看该地址是否为空,空的话就占了它,记录移动次数,不空的话继续向下搜索,直到找到位置。
-
平方探测法:平方探查法的数学描述公式为: d0=h(k) di=(d0± i2) mod m (1≤i≤m-1),平方探查法是一种较好的处理冲突的方法,可以避免出现堆积现象。它的缺点是不能探查到哈希表上的所有单元,但至少能探查到一半单元。
-
哈希链——链地址法:拉链法是把所有的同义词用单链表链接起来的方法。
-
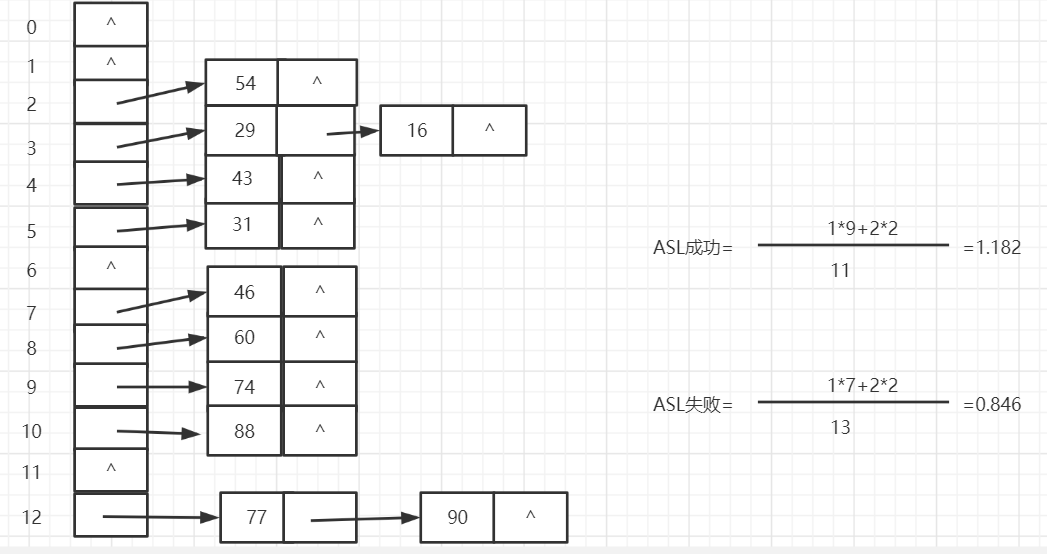
2.PTA题目介绍(0--5分)
2.1 是否完全二叉搜索树(2分)
2.1.1 伪代码(贴代码,本题0分)
typedef struct BNode
{
int data;
struct BNode* left;
struct BNode* right;
}BNode, * BinTree;
全局变量n
main
{
for i to n
输入x
插入函数Insert
endfor
if (Level(BST))
输出yes
else
输出no
}
Insert(BinTree BST, int X)
{
if bst为空
生成新节点然后返回bst
if bst的元素等于x
返回bst
else if bst的元素大于x
BST->right = Insert(BST->right, X);
else if bst的元素小于x
BST->left = Insert(BST->left, X);
}
Level(BinTree BST)//层次遍历
{
count=0,a=1;
queue<BinTree> Q;
BinTree temp;
Q.push(BST);
while 当Q为空停止循环
将Q的第一个元素赋值给temp
if temp不为空
count加一
输出temp的元素
endif
else
if count不等于总元素N
a=0;
endif
continue
endelse
temp的左右子树进队列
endwhile
返回a
}
2.1.2 提交列表

2.1.3 本题知识点
建树,树的插入,树的层次遍历,队列的使用
2.2 航空公司VIP客户查询(2分)
2.2.1 伪代码(贴代码,本题0分)
main
{
初始化哈希链
输入数据 scanf("%d %d", &N, &K);
for 1 to n
输入数据 scanf("%s %d", &str[0], &distance);
if 飞行距离distance小于最小飞行距离k
distance=k
endif
插入函数插入数据到哈希链中
endfor
int M;//要查询的人数
string inquire;
scanf("%d", &M);
for 1 to m
查询人的身份证号码
endfor
}
InsertHash 插入数据到哈希链中
{
取哈希地址
while 遍历链,看它是否飞行过
if 有该人的飞行记录
就把距离加上去
endif
endwhile
用头插法把新数据插入链中
}
Inquire 查询是否该人
{
取哈希地址
while 遍历链直到链为空
if 看看链中是否有要找的人
有就返回并输出距离
endif
endwhile
没找到就输出 No Info
}
2.2.2 提交列表
2.2.3 本题知识点
哈希链的创建,初始化,查找和插入
2.3 基于词频的文件相似度(1分)
2.3.1 伪代码(贴代码,本题0分)
for 1 to n
输入字符串
while 遍历文件直到输入#
for 判断单个文件
if 判断是否字母
如果单词没有达到上限就将单词加入到末尾
endif
endfor
输入下一个字符串
endwhile
endfor
输入m
for 1 to m
输入文件
for 从头到尾遍历文件
if 单词再两个文件都出现过
a和b进行累加
else if 单词再其中一个文件出现过
b单独累加
end
endfor
endfor
输出a/b
2.3.2 提交列表

2.3.3 本题知识点
字符串的遍历,string的使用


 浙公网安备 33010602011771号
浙公网安备 33010602011771号