数据结构与算法（八）-二叉树（斜二叉树、满二叉树、完全二叉树、线索二叉树）

前言：前面了解了树的概念和基本的存储结构类型及树的分类，而在树中应用最广泛的种类是二叉树

一、简介

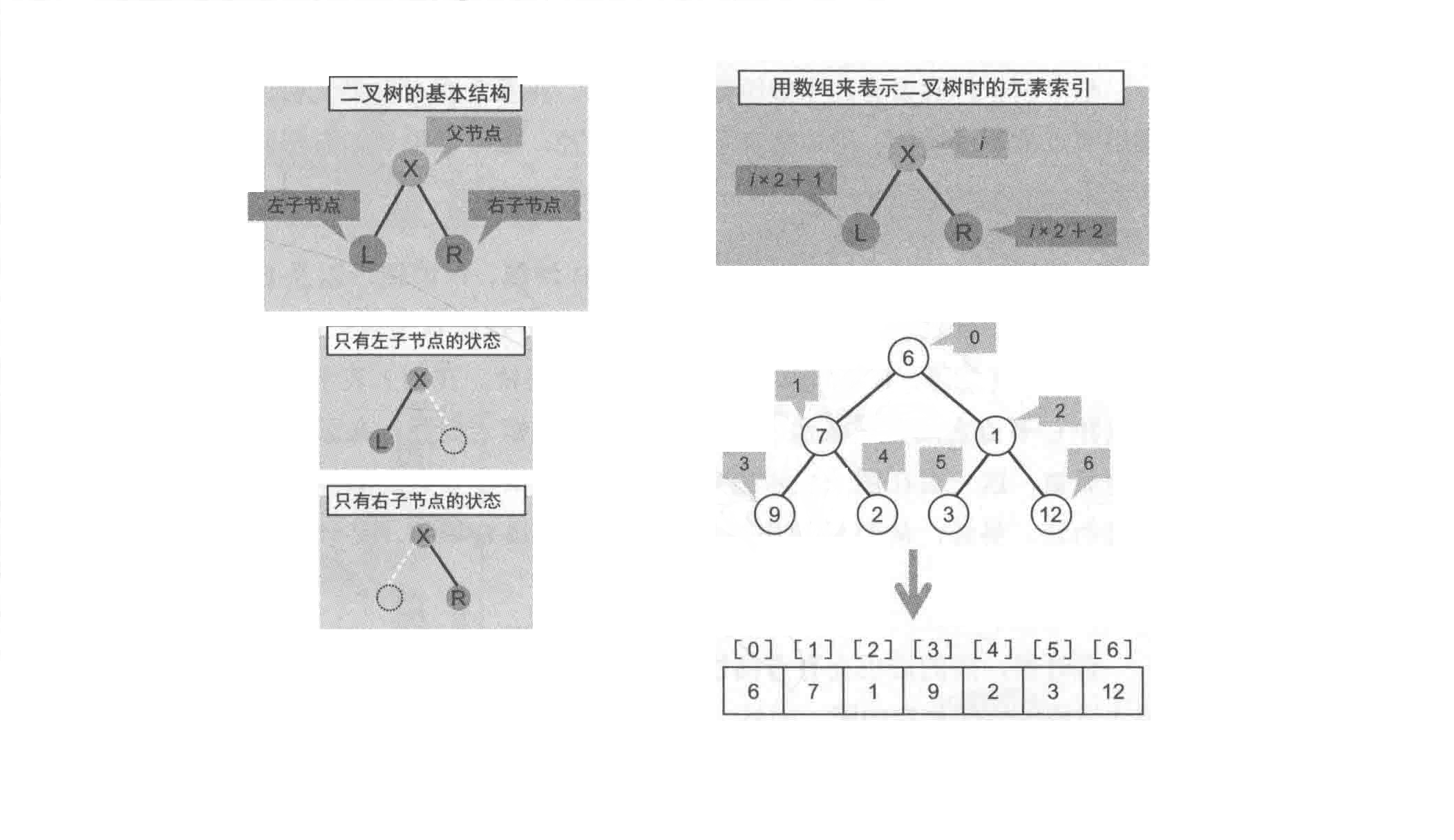
　　在树型结构中，如果每个父节点只有两个子节点，那么这样的树被称为二叉树（Binary tree）。其中，一个父结点的两个字节点分别叫做“左子节点”和“右子节点”。不过也不是所有父节点都有两个子节点，只有左子节点或者只有右子节点的情况也存在。另外，也会存在叶子结点，也就是一个子节点都没有的节点，唯一的限制就是每一个节点的子节点不能超过两个。

　　之前谈过的单向链表，是一种通过“指向下一个元素的指针”来连接各个数据的数据结构，而二叉树则为每一个元素都有两个指向下一个元素的指针。

　　所以二叉树可以使用链表的形式来存储，当然也可以使用数组来表示，可以定义某一个父结点的元素索引是i，并且其左子节点的元素索引为（i×2+1）、右子节点的元素索引为（i×2+2）。例如：将根节点存在了0位置，那么它的左子节点位置为1，右子节点的位置为2，而1位置元素的左子节点为3，右子节点为4，以此类推，可以完整的把二叉树表示出来；

　　二叉树是n（n>=0）个节点的有限集合，该集合可以为空（空二叉树），或由一个根节点和两颗互不相交的、分别称为根节点的左子树和右子树的二叉树组成；

　　这样看来，二叉树可以使用递归来创建。

　　特点：

每个节点最多有两个子节点；
二叉树中最大的度为2；
无论有几个分支，都需要区分是左子树还是右子树；

二、分类及实现

2.1 分类

　　斜二叉树：只有左子节点或只有右子节点的二叉树称为斜二叉树；

　　斜二叉树特点：

度为1；
只有左子节点或右子节点；

　　满二叉树：所有的分支要么左右子节点都有，要么没有子节点，且所有叶子结点都在同一层上；

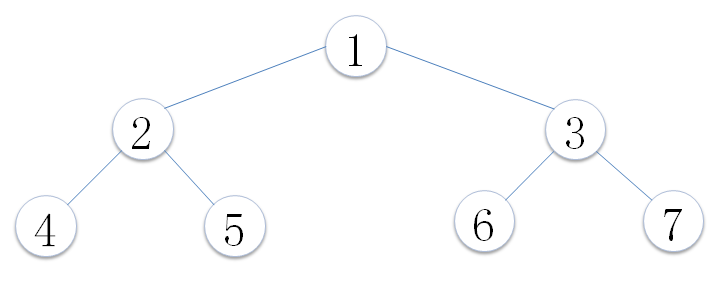
　　满二叉树特点：

叶子结点只能；
非叶子节点的结点的度为2；

　　完全二叉树：对一棵具有n个结点的二叉树按层序编号，如果编号为i(1<=i<=n)的结点与同样深度的满二叉树中编号为i的结点位置完全相同；

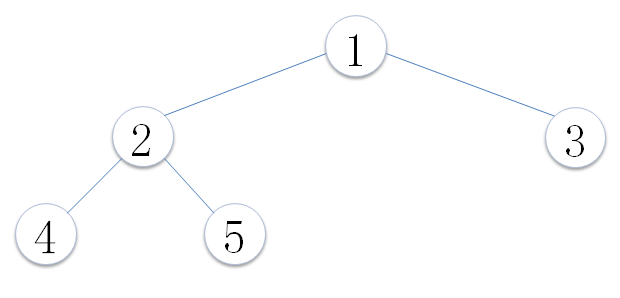
　　完全二叉树特点：

叶子结点只能出现在最下两层；
最下层的叶子结点一定集中在左边并且连续；
若结点度为1，则该节点只有左子节点；

　　注：满二叉树一定是完全二叉树，而完全二叉树不一定是满二叉树；

　　线索二叉树：在空节点中加入了线索（即在某种遍历顺序下指向的下一个节点）指引的二叉树称为线索二叉树；

　　线索二叉树特点：

节省空间，按一定的遍历规则，将空结点的leftNode指向前驱，rightNode指向后继结点；

　　这里先介绍这几种特殊的二叉树，对于平衡二叉树、二叉排序树、红黑树、哈夫曼树想要单独开一篇随笔。

2.2 普通二叉树

2.2.1 二叉树的遍历分类

　　二叉树的遍历是指从根结点出发，按照某种次序依次访问二叉树中所有节点，使得每个节点被访问依次且仅被访问一次。

　　二叉树的遍历次序不同于线性结构，线性结构最多也就是分为顺序、循环、双向等简单的遍历方式。而树不存在唯一的后继节点，在访问一个节点后，下一个被访问的节点面临着不同的选择，所以我们需要规范遍历方式：

　　为了学习遍历方式，我们先创建一个二叉树，如图：

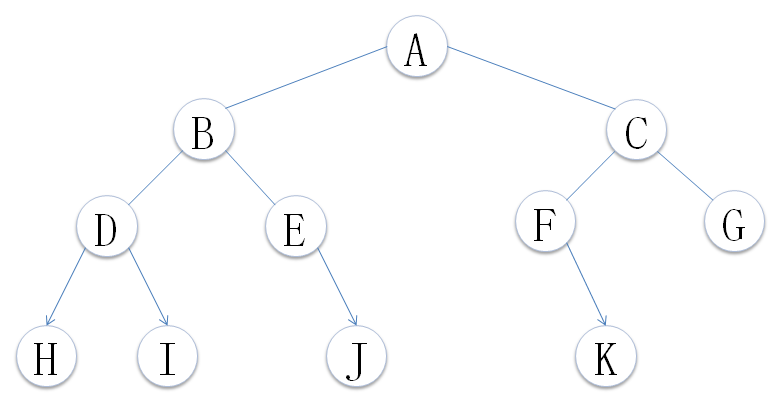
　　①、前序遍历：

　　定义：先访问根节点，然后访问左子树，再访问右子树；

　　按照定义遍历的顺序遍历结果为：A B D H I E J C F K G

　　访问顺序如下图：

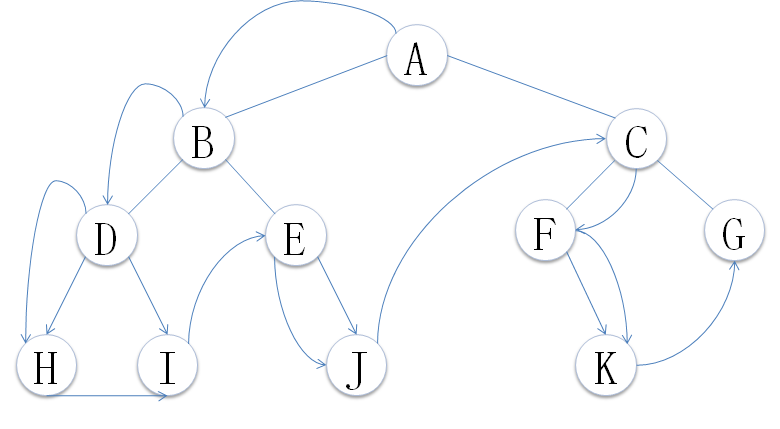
　　②、中序遍历：

　　定义：先访问左子树，再访问根节点，最后访问右子树；

　　按照定义遍历的顺序遍历结果为：H D I B E J A F K C G

　　访问顺序如下图：

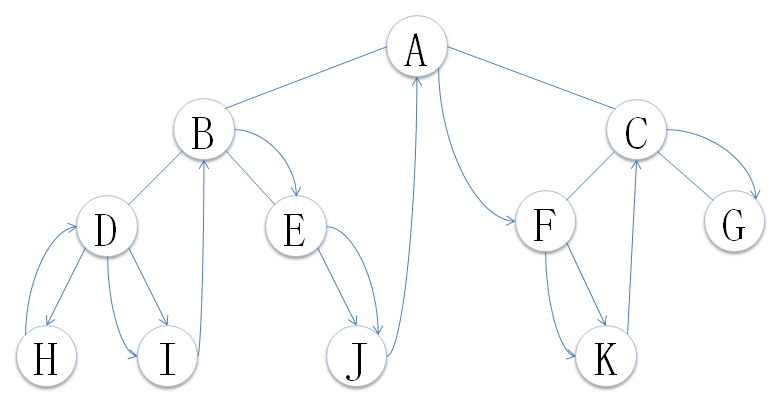
　　③、后序遍历：

　　定义：先访问左子树，再访问右子树，最后访问根节点；

　　按照定义遍历的顺序遍历结果为：H I D J E B K F G C A

　　访问顺序如下图：

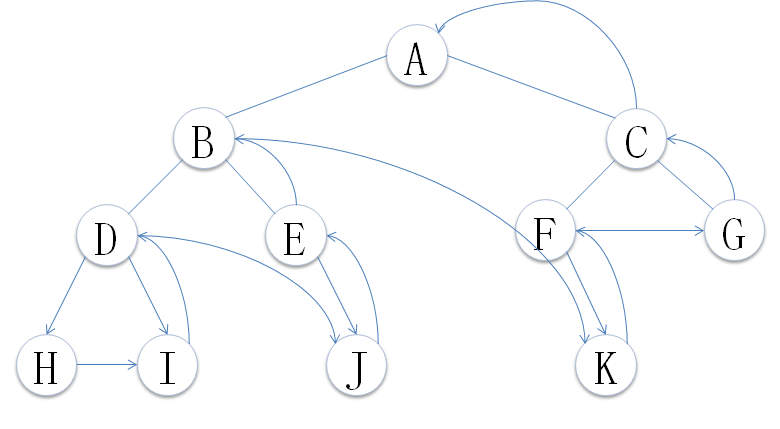
　　④、层次遍历：

　　定义：逐层的从根节点开始，每层从左至右遍历；

　　按照定义遍历的顺序遍历结果为：A B C D E F G H I J K

　　访问顺序如下图：

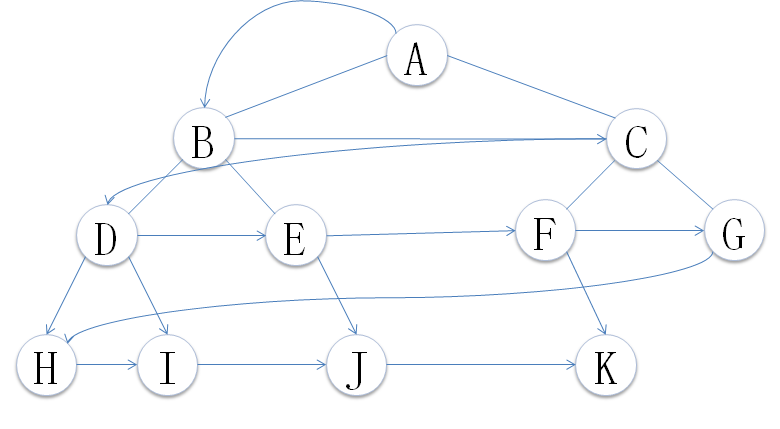
2.2.2 递归

　　程序直接或间接的调用自身的编程技巧称为递归。他通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题方程所需要的多次重复计算，大大地减少了程序的代码量。

　　递归的能力在于用有线的语句来定义对象的无限集合。一般来说，递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时，递归前进；当边界条件满足时，递归返回。

　　例如很有名的斐波那契数列（又称兔子数列，感兴趣的可以了解一下）就可以用递归来解决：

public static Integer getNums(Integer index) {
    //边界条件 
    if (index==1) { 
        return 1; 
    } else if (index==2) { 
        return 1; 
    } else {
        //递归前进 
        return getNums(index - 1) + getNums(index - 2); 
    } 
}

2.2.3 二叉树实现

　　二叉树API：

public class BinaryTree 　　
    BinaryTree()     创建一个空背包 　　
    print()          遍历树
    size()　　　　　　 获取二叉树元素大小 　　
    isEmpty()        是否为空树

　　二叉树的实现需要借助遍历的方式和迭代算法，我们选择前序遍历的方式，并以空格为空叶子节点将字符串转换为二叉树例如：ABDH空格空格I空格空格E空格J空格空格CF空格K空格空格G空格空格（空格代表的是“ ”）。

　　结点Node内部类：

class Node {

        String str;

        Node leftNode;

        Node rightNode;

}

　　创建二叉树代码：

public class BinaryTree {

    private char[] strs;

    private int index;

    private Node root;

    BinaryTree(String str) {
        strs = str.toCharArray();
        root = new Node();
        createBinaryTree(root);
        System.out.println("11");
    }

    private void createBinaryTree(Node node) {
        int currentIndex = index;
        if (currentIndex<strs.length) {
            char str = strs[currentIndex];
            index++;
            if (String.valueOf(str).isEmpty()||str==' ') {
                node.str = null;
            } else {
                node.leftNode = new Node();
                node.rightNode = new Node();
                node.str = String.valueOf(strs[currentIndex]);
                createBinaryTree(node.leftNode);
                createBinaryTree(node.rightNode);
            }
        }
    }
}

BinaryTree.java

　　前序遍历代码：

    public void print() {
        int level = 1;
        iterator(root,level,"根节点");
    }

    private void iterator(Node node, int level, String str) {
        if (node.str==null||node.str.isEmpty()) {

        } else {
            System.out.println(node.str + "在" + level + "层的"+str);
            iterator(node.leftNode,level+1,"左子节点");
            iterator(node.rightNode,level+1,"右子节点");
        }

    }

前序遍历

　　判空和长度方法：

    public Boolean isEmpty() {
        return strs.length < 1;
    }
    
    public int size() {
        return strs.length;
    }

　　书写测试方法：

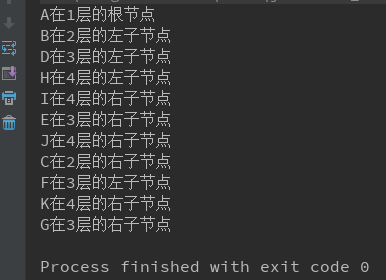
    public static void main(String[] args) {
        BinaryTree tree = new BinaryTree("ABDH  I  E J  CF K  G  ");
        tree.print();
    }

测试结果如图：

2.3 线索二叉树

2.3.1 介绍

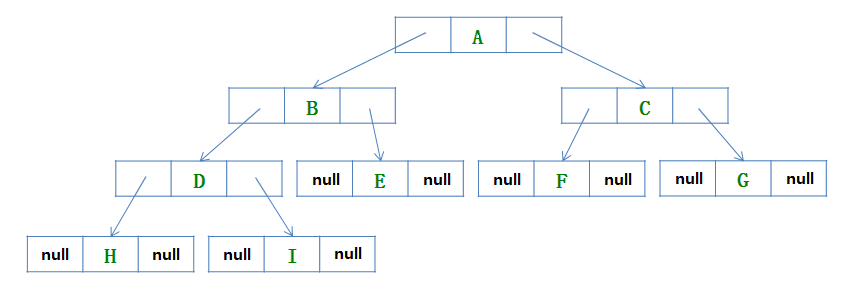
　　在上面普通二叉树的代码实现里，有没有发现叶子节点的leftNode和rightNode为空，而且叶子结点不在少数，那么怎么避免空叶子节点的空间浪费呢？

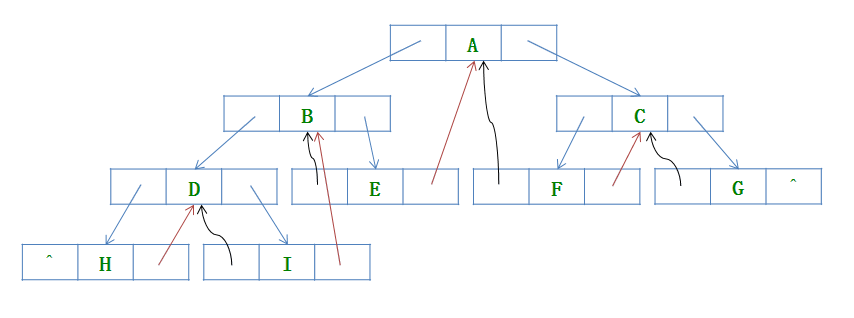
　　而线索二叉树是在上面null的位置放入遍历时的前驱结点和后继结点，如下图：

2.3.2 线索二叉树的实现

　　线索二叉树API：

public class BinaryTree
　　BinaryTree()            创建一个空背包
　　InOrderTraverse()       中序遍历二叉树
　　boolean isEmpty()       是否为空树

　　首先先要改变Node结点的属性结构，增加ltag和rtag来标记是否为线索。

public class ThreadBinaryTread {

    private char[] strs;

    private int index;

    private Node root;

    private Node pre;

    ThreadBinaryTread(String str) {
        strs = str.toCharArray();
        root = new Node();
        createBinaryTree(root);
        //创建完二叉树后，进行二叉树线索化
        Node p = new Node();
        p.ltag = 0;
        p.rtag = 1;
        pre = p;
        inThreading(root);
        pre.rightNode = p;
        pre = p;
    }

    //中序遍历线索化
    private void inThreading(Node node) {
        if (node.str!=null&&!node.str.isEmpty()) {
            inThreading(node.leftNode);
            //如果该节点没有左子节点，则将前一个遍历的结点放入该左子节点的位置并将标志改为线索
            if (node.leftNode.str == null || node.leftNode.str.isEmpty()) {
                node.ltag = 1;
                node.leftNode = pre;
            }

            //如果前一个遍历结点没有右子节点，则将本节点放到前一个节点的右子节点的位置上并将标志改为线索
            if (pre.rightNode==null||pre.rightNode.str==null) {
                pre.rtag = 1;
                pre.rightNode = node;
            }

            pre = node;

            inThreading(node.rightNode);
        }
    }

    private void createBinaryTree(Node node) {
        int currentIndex = index;
        if (currentIndex<strs.length) {
            char str = strs[currentIndex];
            index++;
            if (String.valueOf(str).isEmpty()||str==' ') {
                node.str = null;
            } else {
                node.rightNode = new Node();
                node.leftNode = new Node();
                node.str = String.valueOf(strs[currentIndex]);
                createBinaryTree(node.leftNode);
                createBinaryTree(node.rightNode);
            }
        }
    }

    public void InOrderTraverse() {
        Node node = pre.rightNode;
        while (node!=pre) {
            while (node.ltag==0) {
                node = node.leftNode;
            }
            System.out.println(node.str);
            while (node.rtag==1&&node.rightNode!=pre) {
                node = node.rightNode;
                System.out.println(node.str);
            }
            node = node.rightNode;
        }
    }

    public Boolean isEmpty() {
        return strs.length < 1;
    }

    class Node {

        String str;

        Node leftNode;

        Node rightNode;

        //是否为线索，1：前驱线索；0：左子节点；
        int ltag = 0;

        //是否为线索，1：后继线索；0：右子节点；
        int rtag = 0;

    }

}

ThreadBinaryThread.java

　　创建测试方法：

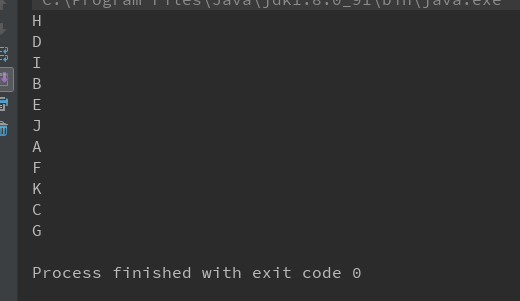
    public static void main(String[] args) {
        ThreadBinaryTread tree = new ThreadBinaryTread("ABDH  I  E J  CF K  G  ");
        tree.InOrderTraverse();
    }

运行结果如图：

三、总结

　　二叉树的特点：

每个节点下最多有两个子节点；
二叉树的度和节点的度最大为2；

　　二叉树遍历的方式：

前序遍历：根节点->左子节点->右子节点;
中序遍历：左子节点->根节点->右子节点;
后序遍历：左子节点->右子节点->根节点;
层次遍历：逐层从左向右遍历;

　　线索二叉树需要线索话才能使用链表的方式遍历；

本系列参考书籍：

　　《写给大家看的算法书》

　　《图灵程序设计丛书算法第4版》

posted @ 2018-09-28 11:11 lfalex 阅读(1848) 评论(0) 编辑收藏举报

刷新页面返回顶部

lfalex

数据结构与算法（八）-二叉树（斜二叉树、满二叉树、完全二叉树、线索二叉树）

一、简介

二、分类及实现

2.1 分类

2.2 普通二叉树

2.2.1 二叉树的遍历分类

2.2.2 递归

2.2.3 二叉树实现

2.3 线索二叉树

2.3.1 介绍

2.3.2 线索二叉树的实现

三、总结

公告