数据结构与算法（二）-线性表之单链表顺序存储和链式存储

前言：前面已经介绍过数据结构和算法的基本概念，下面就开始总结一下数据结构中逻辑结构下的分支——线性结构线性表

一、简介

1、线性表定义

　　线性表（List）：由零个或多个数据元素组成的有限序列；

　　这里有需要注意的几个关键地方：

　　　　1.首先他是一个序列，也就是说元素之间是有个先来后到的。

　　　　2.若元素存在多个，则第一个元素无前驱，而最后一个元素无后继，其他元素都有且只有一个前驱和后继。

　　　　3.线性表强调是有限的，事实上无论计算机发展到多钱大，他所处理的元素都是有限的。

　　使用数学语言来表达的话：

　　　　a1,…,ai-1,ai,ai+1,…an

　　表中ai-1领先于ai,ai领先于ai+1,称ai-1是ai的直接前驱元素,ai+1是ai的直接后继元素。所以线性表元素的各数n（n>0）定义为线性表的长度，当n=0时，称为空表。

2、抽象数据类型

　　数据类型：是指一组性质相同的值得集合及定义在此集合上的一些操作的总称。例如很多编程语言的整型，浮点型，字符型这些指的就是数据类型。

　　不同的数据结构满足不同的计算需求，所以出现了各种各样样的数据类型，它可以分为两类：

　　　　1.原子类型：不可以再分解的基本数据类型，例如整型、浮点型等；

　　　　2.结构类型：有若干个类型组合而成，是可以再分解的，例如整型数组是由若干整型数据组成的；

　　抽象：是指抽取处事务具有的普遍性的本质。他要求抽出问题的特征而忽略非本质的细节，是对具体事务的一个概括。抽象是一种思考问题的方式，他隐藏了复杂的细节。

　　而我们对数据类型进行抽象，就有了抽象数据类型，抽象数据类型是指一个数据模型及定义在该模型上的一组操作。抽象数据类型的定义仅取决于它的一组逻辑特性，而与其在计算机内部如何表示和实现无关。

　　抽象数据类型表示：

ADT 抽象数据类型
　　Data
　　　　数据结构
　　Operation
　　　　具体数据操作（例，增删改查）

　　比如1+1=2这样一个操作，在不同CPU的处理上可能不一样，但由于其定义的数学特性相同，所以在计算机编程者看来，它们都是相同的。“抽象”的意义在于数据类型的数学抽象特性。

　　而且，抽象数据类型不仅仅指那些已经定义并实现的数据类型，还可以是计算机编程者在设计软件程序时自己定义的数据类型。

　　例如一个3D游戏中，要定位角色的位置，那么总会出现x,y,z三个整型数据组合在一起的坐标。我们就可以定义一个point的抽象数据类型，它拥有x,y,z三个整型变量，这样我们就可以方便的对一个角色的位置进行操作。所以抽象数据类型就是把数据类型和相关操作捆绑在一起。

二、线性表实现及优缺点

　　相同的数据逻辑结构可以用不同的存储结构，所以线性表有两种物理存储结构：顺序存储结构和链式存储结构。

1、线性表的顺序存储结构

　　线性表的顺序存储结构，指的是用一段地址连续的存储单元一次存储线性表的数据元素。

　　线性表（a1,a2,……,an）的顺序存储如下：

　　上面的线性表的顺序存储结构是不是与数组一样样的？！？！

　　事实上物理上的存储方式事实上就是在内存中找个初始地址，然后通过占位的形式，把一定的内存空间给占了，然后把相同数据类型的数据元素依次放在这块空地中。

　　总结一下，顺序存储结构封装需要三个属性：

存储空间的起始位置，数组data，它的存储位置就是线性表存储空间的存储位置；
线性表的最大存储容量：数组的长度MaxSize；
线性表的当前长度length；

　　注意：数组的长度与线性表的当前长度需要区分一下。数组的长度是存放线性表的存储空间的总长度，一般初始化后不变。而线性表的当前长度是线性表中元素的个数，是会变化的。

在Java中，它的结构可能是这样的：

public class Linear<T> {

    //存储线性表数据的数组
        private Object[] objects;

        //线性表的长度
        private Integer length;

        //数组的长度
        private Integer objectsLength;

        //初始化
        Linear(Integer objectsLength) {
            objects = new Object[objectsLength];
        }
    
        //查
        public T get(Integer index) {
            return (T)objects[index];
        }

        //增
        public void add(T t) {
　　　　　　　//增加之前先判断是否需要扩容
            isFull();
            objects[length+1]=t;
        }
    
        //删
        public void remove(Integer index) {
            //循环查找index，移除该元素并将后面元素前移一位
        }
    
        //判断当添加一个元素时，是否会数组溢出，若溢出则新建数组并扩大数组长度
        private void isFull() {
        
        } 
}

　　在线性表的顺序存储结构中，它具有随机存储结构的特点，即直接通过下标获取数据或存储，那储它的时间复杂度为O(1)。而当该结构的数据类型做插入操作时，就不能只插入而不管后面的元素，所以插入操作，也要考虑清楚。

插入算法的思路：

如果插入位置不合理，抛出异常；
如果线性表长度大于等于数组长度，则抛出异常活动太增加数组容量；
从最后一个元素开始向前遍历到第i个位置，分别将它们都向后移动一个位置；
将要插入元素填入位置i处；
线性表长+1；

Java代码实现：

public void add(Integer index,T t) throws Exception {
        isFull();
        if (index<0 || index>length)
            throw new Exception("index outof length");
        for (int i = length; i >= index; i--) {
            objects[length+1] = objects[length];
        }
        objects[index] = t;
 }

　　同理，删除元素，也需要将删除元素后的元素依次前移一位；

　　现在分析一下，插入和删除的时间复杂度。

　　最好情况：插入和删除操作刚好要求在最后一个位置操作，因为不需要移动任何元素，所以此时的时间复杂度为O(1)。

　　最坏情况：如果要插入和删除的位置是第一个元素，那就意味着要移动所有的元素向后或者向前，所以这个时间复杂度为O(n)。

　　平均情况，就取中间值O((n-1)/2)。

　　这样来看，平均情况复杂度简化后还是O(n)。

总结：

　　线性表的顺序存储结构，在存、读数据时，不管是哪个位置，时间复杂度都是O(1)。而在插入或删除时，时间复杂度都是O(n)。

　　这就说明，它比较适合元素个数比较稳定，不经常插入和删除元素，而更多的操作是存取数据的应用。

　　我们接下来给大家简单总结下线性表的顺序存储结构的优缺点：

优点：

无需为表中元素之间的逻辑关系而增加额外的存储空间；
可以快速地存取表中任意位置的元素；

缺点：

插入和删除操作需要移动大量元素；
当线性表长度变化较大时，难以确定存储空间的容量；
容易造成存储空间的“碎片”；

2 、线性表的链式存储结构

上一小节介绍了线性表的顺序结构，它最大的缺陷是插入和删除时需要移动大量元素，这是非常耗时的。那我们怎么才能解决这个缺陷呢？这就需要找到原因了。

原因在于顺序存储结构在内存中的位置是连续的、无缝隙的，相邻的存储位置也具有邻居关系，所以当插入和删除时，需要移动大量的元素来保证内存地址的顺序；

而链式的存储结构就不会受内存的存储顺序影响，它可以在任意位置存储，只需要指定元素的后继元素就可以了，也就是说除了存储其本身的信息外，还需存储一个指示其后继的存储位置的信息。

链式存储结构的特点：用一组任意的存储单元存储线性表的数据元素，这组存储单元可以存在内存中未被占用的任意位置。

我们把存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域。指针域中存储的信息称为指针或链。这两部分信息组成数据类型称为存储映像，也成为结点(Node)。

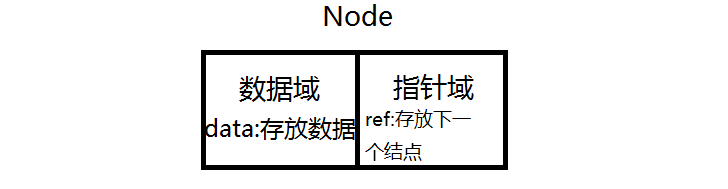
Java代码来表示结点：

class Node<T> {

　　private Object object;

　　private Node next;

　　public Object getObject() {
　　　　return object;
　　}

　　public void setObject(Object object) {
　　　　this.object = object;
　　}

　　public Node getNext() {
　　　　return next;
　　}

　　public void setNext(Node next) {
　　　　this.next = next;
　　}

}

单链表结构图：

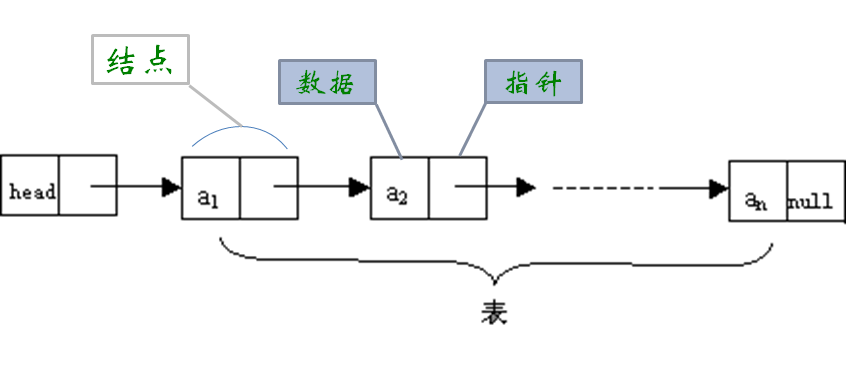
对于线性表来说，总得有个头有个尾，链表也不例外。我们把链表中的第一个结点的存储位置叫做头指针，最后一个结点指针为空(NULL)。

头指针：

头指针是指链表指向第一个节点的指针，若链表有头结点，则是指向头结点的指针；
头指针具有表示作用，所以常用头指针冠以链表的名字(指针变量的名字)；
无论链表是否为空，头指针均不为空；
头指针是链表的必要元素

头结点：

头结点是为了操作的统一和方便而设立的，放在第一个元素的结点之前，其数据域一般无意义（但也可以用来存放链表的长度）；
有了头结点，对在第一元素结点前插入结点和删除第一结点起操作与其它结点的操作就统一了；
头节点不一定是链表的必要元素；

Java代码：

public class Chain<T> {

　　//头结点直接引用
　　private Node<T> head;

　　//初始化
　　Chain() {
　　　　head = new Node<T>();
　　　　head.setNext(null);
　　}

　　class Node<T> {

　　　　...
　　}

}

　　在顺序存储结构中，有随机存储结构的特点，计算任意一个元素的存储位置是很容易的，但是在单链表中，想知道其中一个元素的位置，就得从第一个结点开始遍历，因此，对于单链表实现获取第i个元素的数据的操作，在算法上较为复杂。

　　获取链表第i个数据的算法思路：

声明一个节点p指向链表第一个节点，初始化j从1开始；
当j<i时，酒便利链表，让p的指针向后移动，不断指向下一个节点，j+1；
若到链表末尾p为空，则说明第i个元素不存在；
否则查找成功，返回节点p的数据；

单链表数据的获取：

public T get(Integer index) throws Exception {
    return (T)getNode(index).getObject();
}

private Node<T> getNode(Integer index) throws Exception {
    if (index > size || index < 0)
        throw new Exception("index outof length");
    Node<T> p = head;
    for (int i = 0; i < index; i++)
        p = p.next;
    return p;
}

　　由于这个算法的时间复杂度取决于i的位置，当i=1时，则不需要遍历，而i=n时则遍历n-1次才可以。因此最坏情况的时间复杂度为O(n)。

　　在Java中有运用到线性的链式存储结构的类LinkedList。查看源码，在该类中的获取节点的方法比较巧妙：

Node<E> node(int index) {
    //通过比较下标在list中的位置，来决定是从前往后还是从后往前遍历，以提高效率
    if (index < (size >> 1)) {
        Node<E> x = first;
        for (int i = 0; i < index; i++)
            x = x.next;
        return x;
    } else {
        Node<E> x = last;
        for (int i = size - 1; i > index; i--)
            x = x.prev;
        return x;
    }
}

　　Java中的算法需要Node类中有前置节点（也就是双向链表，后面会介绍），这样可以从后面向前便利，提升性能，它的时间复杂度为O(size-n)或O(n),也就是空间换时间。

单链表的插入：

创建新的结点p；
将新节点p的next指向当前节点s的next；
将当前结点s的next指向新节点p；
完成插入；

Java代码：

public void add(T t,Integer index) throws Exception {
    //获取该位置的上一个节点
    Node<T> s = getNode(index - 1);
    //创建新节点
    Node<T> p = new Node<>();
    p.setObject(t);
    //将本节点的next节点放入新节点的next节点
    p.setNext(s.getNext());
    //将新节点放入本节点的next节点位置
    s.setNext(p);
}

而单链表的删除与插入本质是相同的，无非一个是放，一个是拿，所以直接上代码：

public Node<T> remove(Integer index) throws Exception {
    //获取该位置的上一个节点
    Node<T> s = getNode(index - 1);
    //获取该位置节点的下一个节点
    Node<T> next = getNode(index).getNext();
    //将本节点的next节点放在本节点的前一个节点的next节点位置
    s.setNext(next.getNext());
    return next;
}

我们发现无论是单链表插入还是删除算法，他们其实都是由两部分组成：

遍历查找第i个元素；
实现插入和删除元素；

　　从整个算法来说，我们很容易可以推算出他们的时间复杂度都是O(n)。再详细点分析：

　　　　如果在我们不知道第i个元素的指针位置，单链表数据结构在插入和删除操作上，与线性表的顺序存储结构是没有太大优势的。

　　但是，如果我们从第i个位置连续插入10个、100个等等很多元素时，对于顺序存储结构意味着，每一次插入都需要移动n-i个位置，所以每次都是O(n)。而单链表，我们只需要在第一次时，找到第i个位置的指针，此时为O(n)，接下来只是简单地通过赋值移动指针而已，时间复杂度都是O(1)。

　　显然，对于插入或删除数据越纷繁复杂的操作越多，单链表的性能优势就越是明显。

头插法：

　　头插法从一个空表开始，生成新结点，读取数据存放到新结点的数据域中，然后将新结点插入到当前链表的表头上，直到结束为止。

　　简单来说，就是把新加进的元素放在表头后的第一个位置：

先让新节点的next指向头结点之后；
然后让表头的next指向新节点；

　　这样插入的时间复杂度为O(1)。

尾插法：

　　需要一个引用时刻记录链表的尾节点，这样插入时直接插入，以提升性能。

3 、总结

存储分配方式：

顺序存储结构用一段连续的存储单元依次存储线性表的数据元素；
单链表采用链式存储结构，用一组任意的存储单元存放线性表的元素；

时间性能：

查找

顺序存储结构O(1)；
单链表O(n);

插入和删除

顺序存储结构需要平均移动表唱一半的元素，时间为O(n)；
单链表在计算出某位置的指针后，插入和删除时间仅为O(1)；

空间性能：

顺序存储结构需要预分配存储空间，分多了，容易造成空间浪费，分少了，容易溢出；
单链表不需要分配存储空间，只要有就可以分配，元素个数也不瘦限制；

结论：

若需要频繁查找，很少进行插入和删除操作时，宜采用顺序存储结构；
若需要频繁插入和删除时，宜采用单链表结构；

说句题外话，Java中的ArrayList和LinkedList分别对应的存储结构为顺序和链式，所以这两个类也适用这个结论。

本系列参考书籍：

　　《写给大家看的算法书》

　　《图灵程序设计丛书算法第4版》

posted @ 2018-09-20 09:32 lfalex 阅读(6091) 评论(2) 编辑收藏举报

刷新页面返回顶部

lfalex

数据结构与算法（二）-线性表之单链表顺序存储和链式存储

一、简介

1、线性表定义

2、 抽象数据类型

二、线性表实现及优缺点

1、 线性表的顺序存储结构

2 、 线性表的链式存储结构

3 、 总结

公告

2、抽象数据类型

1、线性表的顺序存储结构

2 、线性表的链式存储结构

3 、总结