Stanford机器学习---第一讲. Linear Regression with one variable(补充版)
注：由Leytton修改，按照自己学习2014年版的machine learning课程理解，添加了部分更详细说明，如有不对恳请指正
原文摘自 http://blog.csdn.net/abcjennifer/article/details/7691571
本栏目（Machine learning）包括单参数的线性回归、多参数的线性回归、Octave Tutorial、Logistic Regression、Regularization、神经网络、机器学习系统设计、SVM（Support Vector Machines 支持向量机）、聚类、降维、异常检测、大规模机器学习等章节。所有内容均来自Standford公开课machine learning中Andrew Ng老师的讲解。（https://class.coursera.org/ml/class/index ）
找不到可在https://class.coursera.org搜索课程Machine
Learning 可到我的网盘打包下载 http://pan.baidu.com/s/1ntHmO6d
第一章-------单参数线性回归 Linear Regression with one variable
(二)、Cost Function
线性回归是给出一系列点假设拟合直线为h(x)=θ0+θ1*x, 记Cost Function为J(θ0,θ1)
把已知样本数据x0,x1,x2...代入h(x)，会得到预测值y0',y1',y2'... 会与真实值有一定误差,
用方差表示,把所有误差值相加,求平均值就是2*J(θ0,θ1) [J(θ0,θ1)见下图]，为使后面平方求导后消去,故Cost Function系数有1/2
之所以说单参数是因为只有一个变量x，即影响回归参数θ1,θ0的是一维变量，或者说输入变量只有一维属性。
下图中为简化模式，只有θ1没有θ0的情况，即拟合直线为h(x)=θ1*x
左图为给定θ1时的直线和数据点×
右图为不同θ1下的cost function J(θ1)
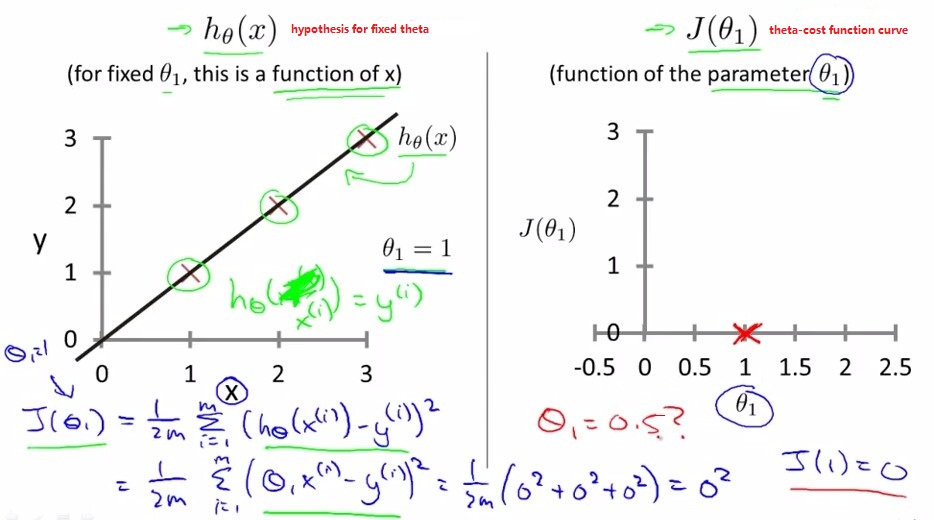
cost function plot:
当存在两个参数theta0和theta1时，cost function是一个三维函数，这种样子的图像叫bowl-shape function
将上图中的cost function在二维上用不同颜色的等高线映射为如下右图，可得在左图中给定一个(theta0,theta1)时又图中显示的cost function.
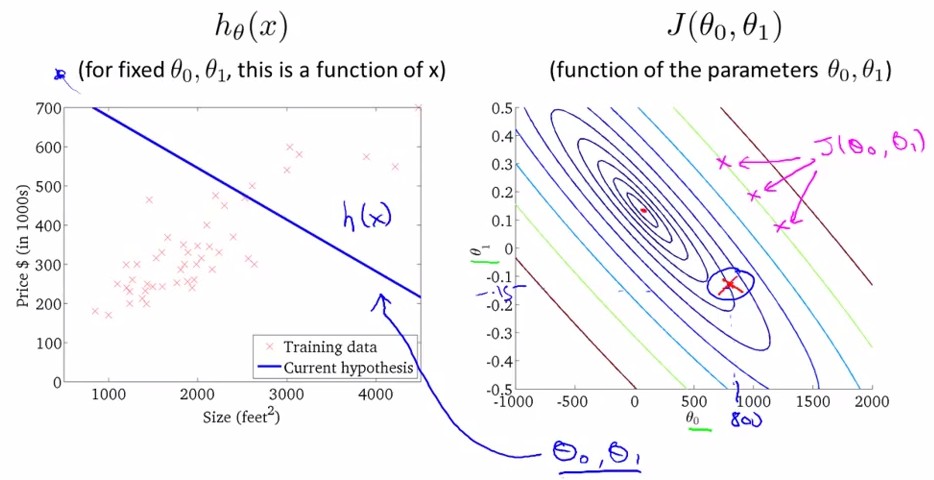
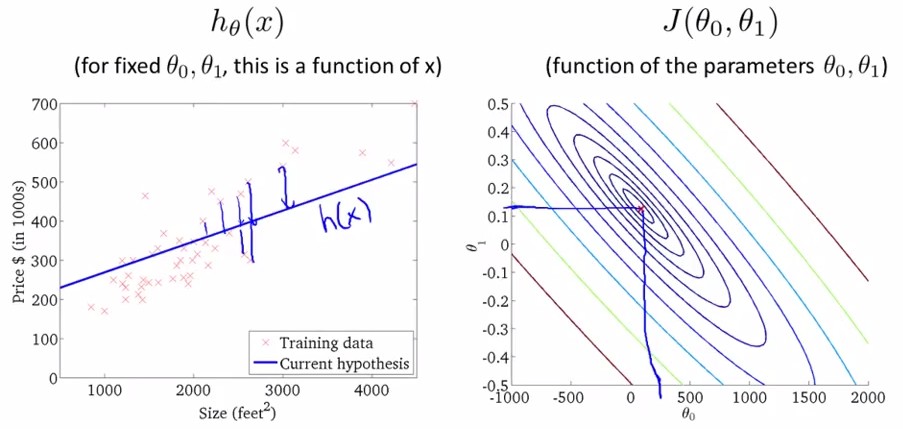
我们的目的是最小化cost function,即上图中最后一幅图，theta0=450,theta1=0.12的情况。
（三）、Gradient descent
gradient descent是指梯度下降，为的是将cost funciton 描绘出之后，让参数沿着梯度下降的方向走，并迭代地不断减小J(theta0，theta1)，即稳态。
每次沿着梯度下降的方向：
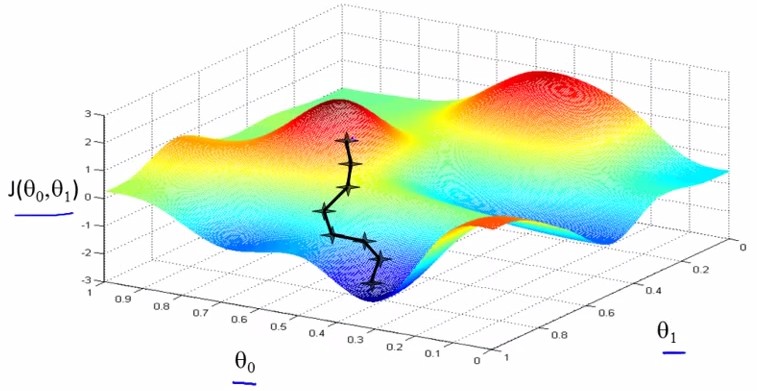
参数的变换公式：其中标出了梯度（蓝框内）和学习率（α）：
下降最快的方式便是沿着切线方向下降，因而对其所在点进行求导
gradient即J在该点的切线斜率slope，tanβ。下图所示分别为slope（gradient）为正和负的情况：
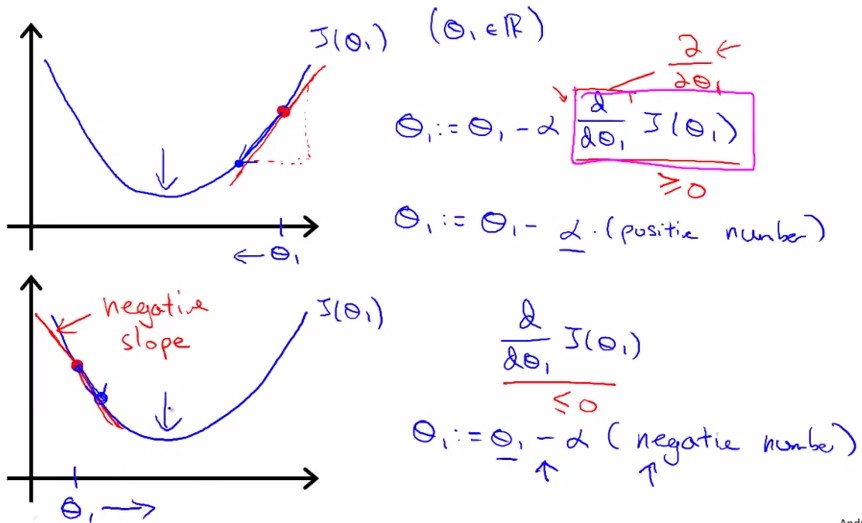
同时更新theta0和theta1，左边为正解：
关于学习率:
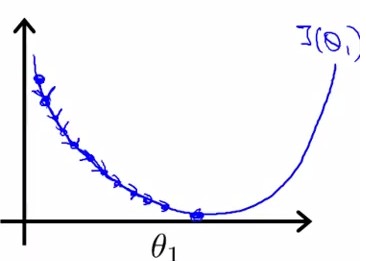
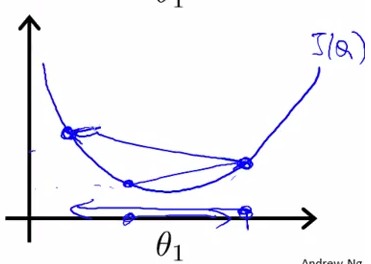
α太小：学习很慢； α太大：容易过学习
所以如果陷入局部极小，则slope=0，不会向左右变换
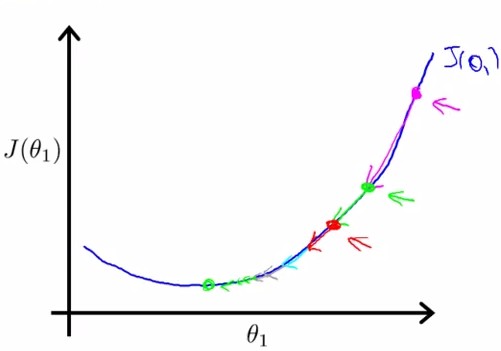
本图表示：无需逐渐减小α，就可以使下降幅度逐渐减小（因为梯度逐渐减小）：
求导后：
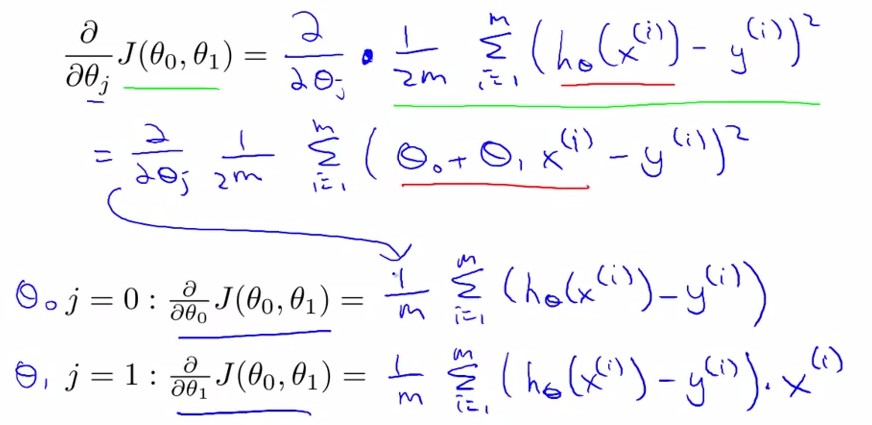
由此我们得到：
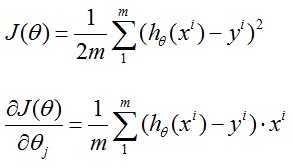
其中x(i)表示输入数据x中的第i组数据
