《比你见过的所有古典密码概述都细?没错,就是这篇!》
古典密码
古典密码的概念
古典密码是密码学发展的早期阶段,主要包括置换密码和代换密码两大类。
古典密码的定义
古典密码是指 1976 年以前的密码算法,主要通过手工或简单的机械操作进行信息的加密和解密。其核心思想是通过替换和置换来隐藏信息的真实内容。
古典密码的分类
置换密码:将明文中的字符重新排列,字母本身不变,但其位置改变了,这样编成的密码称为置换密码。最简单的置换密码是把明文中的字母顺序倒过来,然后截成固定长度的字母组作为密文。 代换密码:将明文中的字符替代成其他字符。代换密码又可分为单表代换密码和多表代换密码。 单表代换密码:如凯撒密码,通过将字母表中的每个字母移动固定位置来实现加密。 多表代换密码:如维吉尼亚密码,使用一个关键词来控制字母的替换。
古典密码的常见算法
凯撒密码
通过将字母表中的每个字母移动固定位置来实现加密,是最简单的替换密码之一。
凯撒密码(英语:Caesar cipher),或称凯撒加密、凯撒变换、变换加密,是一种最简单且最广为人知的加密技术。凯撒密码是一种替换加密技术,明文中的所有字母都在字母表上向后(或向前)按照一个固定数目进行偏移后被替换成密文。例如,当偏移量是 3 的时候,所有的字母 A 将被替换成 D,B 变成 E,以此类推。这个加密方法是以罗马共和时期凯撒的名字命名的,据称当年凯撒曾用此方法与其将军们进行联系。
凯撒密码通常被作为其他更复杂的加密方法中的一个步骤,例如维吉尼亚密码。凯撒密码还在现代的 ROT13 系统中被应用。但是和所有的利用字母表进行替换的加密技术一样,凯撒密码非常容易被破解,而且在实际应用中也无法保证通信安全。
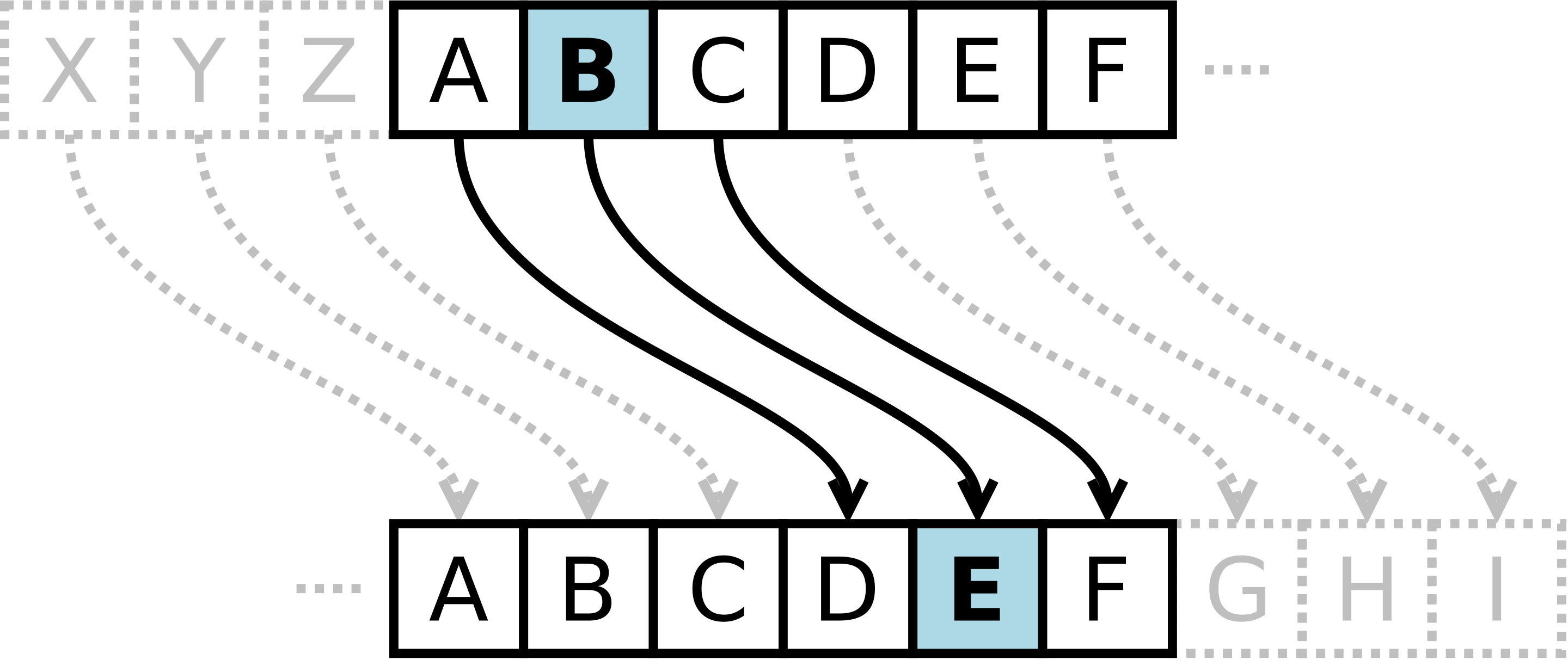
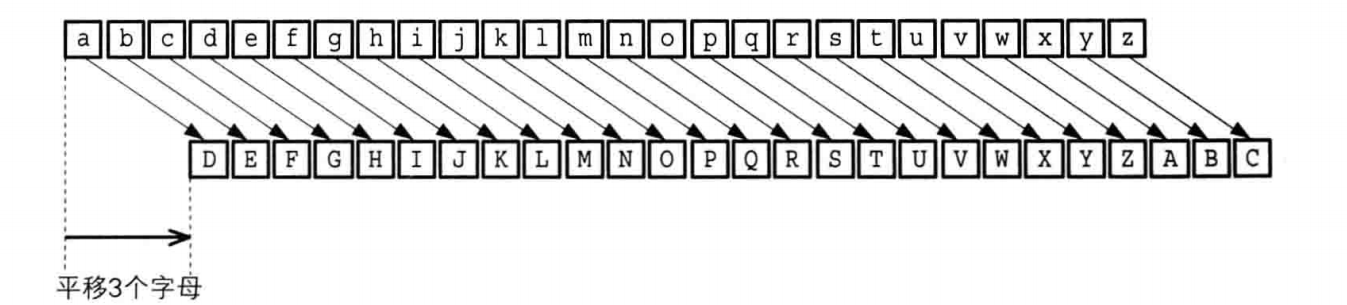
当偏移量是 3 的时候,所有的字母 A 将被替换成 D,B 变成 E,以此类推。
eg: 凯撒密码的替换方法是通过排列明文和密文字母表,密文字母表示通过将明文字母表向左或向右移动一个固定数目的位置。例如,当偏移量是左移 3 的时候(解密时的密钥就是 3):
使用时,加密者查找明文字母表中需要加密的消息中的每一个字母所在位置,并且写下密文字母表中对应的字母。需要解密的人则根据事先已知的密钥反过来操作,得到原来的明文。例如:
凯撒密码的加密、解密方法还能够通过同余的数学方法进行计算。首先将字母用数字代替,A=0,B=1,...,Z=25。此时偏移量为 n 的加密方法即为:
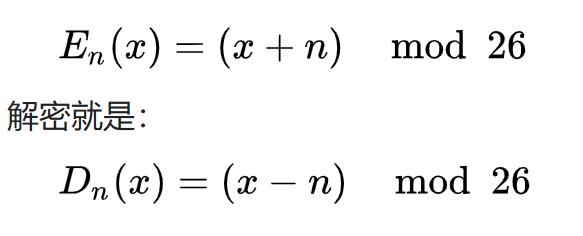
特定凯撒密码名称
根据偏移量的不同,还存在若干特定的凯撒密码名称:
偏移量为 10:Avocat(A→K) 偏移量为 13:ROT13 偏移量为-5:Cassis (K 6) 偏移量为-6:Cassette (K 7)
密码破解
即使使用唯密文攻击,凯撒密码也是一种非常容易破解的加密方式。可能有两种情况需要考虑:
攻击者知道(或者猜测)密码中使用了某个简单的替换加密方式,但是不确定是凯撒密码; 攻击者知道(或者猜测)使用了凯撒密码,但是不知道其偏移量。 对于第一种情况,攻击者可以通过使用诸如频率分析或者样式单词分析的方法,马上就能从分析结果中看出规律,得出加密者使用的是凯撒密码。 对于第二种情况,解决方法更加简单。由于使用凯撒密码进行加密的语言一般都是字母文字系统,因此密码中可能是使用的偏移量也是有限的,例如使用 26 个字母的英语,它的偏移量最多就是 25(偏移量 26 等同于偏移量 0,即明文;偏移量超过 26,等同于偏移量 1-25)。因此可以通过穷举法,很轻易地进行破解[6]。其中一种方法是在表格中写下密文中的某个小片段使用所有可能的偏移量解密后的内容——称为候选明文,然后分析表格中的候选明文是否具有实际含义,得出正确的偏移量,解密整个密文。例如,被选择出的密文片段是"EXXEGOEXSRGI",可以从右表中的候选明文里很快看出其正确的偏移量是 4。也可以通过在每一个密文单词的每一个字母下面,纵向写下整个字母表其他字母,然后可以通过分析,得出其中的某一行便是明文。
另外一种攻击方法是通过频率分析。当密文长度足够大的情况下,可以先分析密文中每个字母出现的频率,然后将这一频率与正常情况下的该语言字母表中所有字母的出现频率做比较。例如在英语中,正常明文中字母 E 和 T 出现的频率特别高,而字母 Q 和 Z 出现的频率特别低,而在法语中出现频率最高的字母是 E,最低的是 K 和 W。可以通过这一特点,分析密文字母出现的频率,可以估计出正确的偏移量。此外,有时还可以将频率分析从字母推广到单词,例如英语中,出现频率最高的单词是[7]:the, of, and, a, to, in...。通过将最常见的单词的所有可能的 25 组密文,编组成字典,进行分析。比如 QEB 可能是 the,MPQY 可能是单词 know(当然也可能是 aden)。但是频率分析也有其局限性,它对于较短或故意省略元音字母或者其他缩写方式写成的明文加密出来的密文进行解密并不适用。
| 偏移量 | 候选明文 |
|---|---|
| 0 | exxegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attackatonce |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| …………………………… | ……………………………… |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
另外,通过多次使用凯撒密码来加密并不能获得更大的安全性,因为使用偏移量 A 加密得到的结果再用偏移量 B 加密,等同于使用 A+B 的偏移量进行加密的结果。
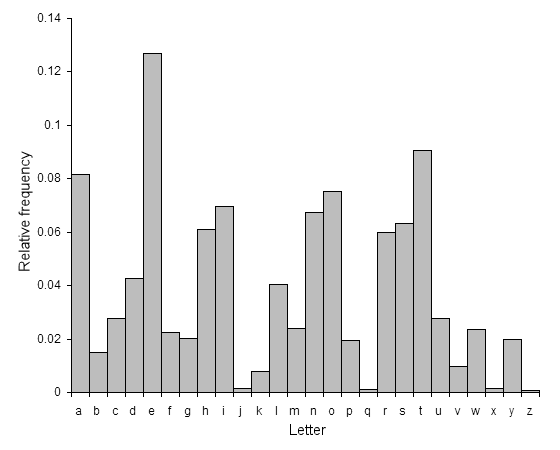 用典型的英语书写的文字样本中各字母出现频率
用典型的英语书写的文字样本中各字母出现频率
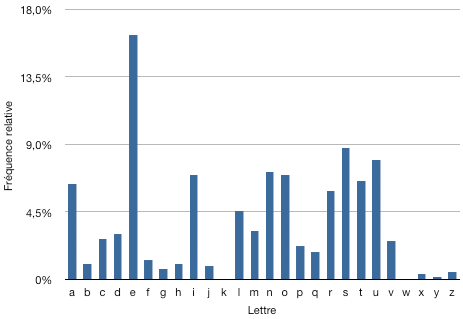 用典型的法语书写的文字样本中各字母出现频率
用典型的法语书写的文字样本中各字母出现频率
维吉尼亚密码
使用一个关键词来对明文进行多表替换加密,是古典密码中较为复杂的一种。
维吉尼亚密码(法语:Chiffre de Vigenère,又译维热纳尔密码)是使用一系列凯撒密码组成密码字母表的加密算法,属于多表密码的一种简单形式。
维吉尼亚密码曾多次被发明。该方法最早记录在吉奥万·巴蒂斯塔·贝拉索( Giovan Battista Bellaso)于 1553 年所著的书《吉奥万·巴蒂斯塔·贝拉索先生的密码》(意大利语:La cifra del. Sig. Giovan Battista Bellaso)中。然而,后来在 19 世纪时被误传为是法国外交官布莱斯·德·维吉尼亚(Blaise De Vigenère)所创造,因此现在被称为“维吉尼亚密码”。
维吉尼亚密码以其简单易用而著称,同时初学者通常难以破解,因而又被称为“不可破译的密码”(法语:le chiffre indéchiffrable)。这也让很多人使用维吉尼亚密码来加密的目的就是为了将其破解。 在一个凯撒密码中,字母表中的每一字母都会作一定的偏移,例如偏移量为 3 时,A 就转换为了 D、B 转换为了 E……而维吉尼亚密码则是由一些偏移量不同的凯撒密码组成。
为了生成密码,需要使用表格法。这一表格包括了 26 行字母表,每一行都由前一行向左偏移一位得到。具体使用哪一行字母表进行编译是基于密钥进行的,在过程中会不断地变换。
例如,假设明文为:
选择某一关键词并重复而得到密钥,如关键词为 LEMON 时,密钥为:
对于明文的第一个字母 A,对应密钥的第一个字母 L,于是使用表格中 L 行字母表进行加密,得到密文第一个字母 L。类似地,明文第二个字母为 T,在表格中使用对应的 E 行进行加密,得到密文第二个字母 X。以此类推,可以得到:
解密的过程则与加密相反。
eg: 根据密钥第一个字母 L 所对应的 L 行字母表,发现密文第一个字母 L 位于 A 列,因而明文第一个字母为 A。密钥第二个字母 E 对应 E 行字母表,而密文第二个字母 X 位于此行 T 列,因而明文第二个字母为 T。以此类推便可得到明文。
用数字 0-25 代替字母 A-Z,维吉尼亚密码的加密文法可以写成同余的形式:

密码破解
对包括维吉尼亚密码在内的所有多表密码的破译都是以字母频率为基础的,但直接的频率分析却并不适用。例如,如果 P 是密文中出现次数最多的字母,则 P 很有可能对应 E(前提是明文的语言为英语)。原因在于 E 是英语中使用频率最高的字母。然而,由于在维吉尼亚密码中,E 可以被加密成不同的密文,因而简单的频率分析在这里并没有用。
破译维吉尼亚密码的关键在于它的密钥是循环重复的。如果我们知道了密钥的长度,那密文就可以被看作是交织在一起的凯撒密码,而其中每一个都可以单独破解。使用卡西斯基试验和弗里德曼试验来得到密钥的长度。
卡西斯基试验 弗里德里希·卡西斯基于 1863 年首先发表了完整的维吉尼亚密码的破译方法,称为卡西斯基试验(Kasiski examination)。早先的一些破译都是基于对于明文的认识、或者使用可识别的词语作为密钥。而卡西斯基的方法则没有这些限制。然而,在此之前,已经有人意识到了这一方法。1854 年,英国数学家、发明家兼机械工程师查尔斯·巴贝奇受到斯维提斯(John Hall Brock Thwaites)在《艺术协会杂志》(Journal of the Society of the Arts)上声称发明了“新密码”的激励,从而破译了维吉尼亚密码。巴贝奇发现斯维提斯的密码只不过是维吉尼亚密码的一个变种而已,而斯维提斯则向其挑战,让他尝试破译用两个不同长度的密钥加密的密文。巴贝奇成功地进行了破译,得到的明文是丁尼生所写的诗《罪恶的想象》(The Vision of Sin),使用的密钥则是丁尼生妻子的名字 Emily(艾米莉)。巴贝奇从未对他的方法进行过解释 。在对巴贝奇生前笔记的研究中发现,早在 1846 年巴贝奇就使用了这一方法,与后来卡西斯基发表的方法相同。
卡西斯基试验是基于类似 the 这样的常用单词有可能被同样的密钥字母进行加密,从而在密文中重复出现。例如,明文中不同的 CRYPTO 可能被密钥 ABCDEF 加密成不同的密文:
此时明文中重复的元素在密文中并不重复。然而,如果密钥相同的话,结果可能便为(使用密钥 ABCD):
此时卡西斯基试验就能产生效果。对于更长的段落此方法更为有效,因为通常密文中重复的片段会更多。如通过下面的密文就能破译出密钥的长度:
其中,两个 DYDUXRMH 的出现相隔了 18 个字母。因此,可以假定密钥的长度是 18 的约数,即长度为 18、9、6、3 或 2。而两个 NQD 则相距 20 个字母,意味着密钥长度应为 20、10、5、4 或 2。取两者的交集,则可以基本确定密钥长度为 2。
弗里德曼试验 弗里德曼试验由威廉·F·弗里德曼(William F. Friedman)于 1920 年代发明。他使用了重合指数(index of coincidence)来描述密文字母频率的不匀性,从而破译密码。 κp 指目标语言中两个任意字母相同的概率(英文中为 0.067), κr 指字母表中这种情况出现的概率(英文中为 1/26=0.0385),从而密钥长度可以估计为:
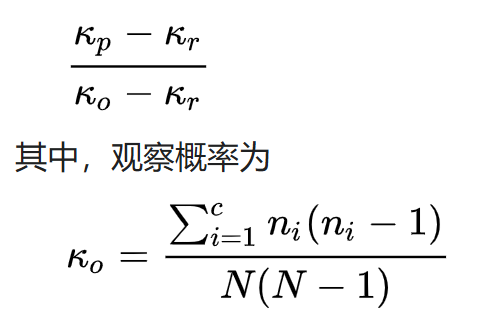 其中,c 是指字母表的长度(英文为 26),N 指文本的长度,n1 到 nc 是指密文的字母频率,为整数。
其中,c 是指字母表的长度(英文为 26),N 指文本的长度,n1 到 nc 是指密文的字母频率,为整数。
此方法只是一种估计,会随着文本长度的增加而更为精确。在实践中,会尝试接近此估计的多个密钥长度。一种更好的方法是将密文写成矩阵形式,其中列数与假定的密钥长度一致,将每一列的重合指数单独计算,并求得平均重合指数。对于所有可能的密钥长度,平均重合指数最高的最有可能是真正的密钥长度。这样的试验可以作为卡西斯基试验的补充。
频率分析: 一旦能够确定密钥的长度,密文就能重新写成多列,列数与密钥长度对应。这样每一列其实就是一个凯撒密码,而此密码的密钥(偏移量)则对应于维吉尼亚密码密钥的相应字母。与破译凯撒密码类似的方法,就能将密文破译。
柯克霍夫方法作为卡西斯基试验的改进,由奥古斯特·柯克霍夫(Auguste Kerckhoffs)提出。它将每一列的字母频率与转换后的明文频率相对应而得出每一列的密钥字母。一旦密钥中每一个字母都能确定,就能很简单地破译密文,从而得到明文。如果维吉尼亚字母表表格本身是杂乱而非按通常字母表顺序的话,那柯克霍夫方法就会无效,但卡西斯基试验和重复指数对于决定密钥长度仍旧是有效的。
维吉尼亚密码的变体
维吉尼亚密码的变体滚动密钥密码也曾一度被认为是不可破译的。这种变体的密钥与密文的长度一致,因此卡西斯基试验和弗里德曼试验即变得无效。1920 年,弗里德曼首先发现了此方法的弱点。由于滚动密钥密码的密钥是一段真实的语言,因而破译者便能了解密钥文本的统计信息,而这种信息也会反映到密文当中。 如果密钥是完全随机、与明文的长度一致且只使用过一次,维吉尼亚密码理论上是不可破译的。然而,这种情况下密钥本身而非密文便成了关键,这被称为一次性密码本。 维吉尼亚本人确实发明了一种更强的维吉尼亚密码变体——自动密钥密码。巴贝奇所破译的其实是这种自动密钥密码,而卡西斯基则通常被认为是首先发表了破译固定密钥多表密码的方法。 还有一种简单的变体使用维吉尼亚的解码方法进行加密,同时使用维吉尼亚的加密方法进行解密,这被称为变异博福特密码。此方法与弗朗西斯·博福特创造的博福特密码不同,后者虽然也与维吉尼亚密码相似,但使用了修改过的加密方式和表格,是一种对等加密。 维吉尼亚密码表面上的强度并没能使其在欧洲得到广泛使用。由 Gronsfeld 伯爵所创造的 Gronsfeld 密码基本与维吉尼亚密码相同,不过它只使用 10 个不同的密码字母表(对应字母 0 到 9)。Gronsfeld 密码的强度很高,这是因为它的密钥并不是一个单词,但缺点在于字母表数量过少。尽管如此,Gronsfeld 密码仍在德国和整个欧洲有着广泛的应用。
栅栏密码
将明文按列写入,密文按行输出,通过置换字母的位置来加密。
栅栏密码是古典密码的一种,其原理是将一组要加密的明文划分为 n 个一组(n 通常根据加密需求确定,且一般不会太大,以保证密码的复杂性和安全性),然后取每个组的第一个字符(有时也涉及取其他位置的字符,但规则需事先约定),根据情况将这些字符重新排列组合成一段无规律的话,形成密文。
栅栏密码的“栏”数,即分组后形成的“列”数或“行”数(具体取决于加密时的排列方式),是栅栏密码的一个重要参数。根据栏数的不同,栅栏密码可以分为多种类型,其中比较常见的是 2 栏栅栏密码。但理论上,栏数 n 可以是任何正整数(实际应用中受限于明文的长度和加密的安全性要求)。
加密原理
分栏:首先将需要加密的明文(即原始信息)中的字母交替排成多行(通常称为“栏”),栏数可以是任意的,但通常不会超过 30 个字母(大约一两句话的长度)
重新组合:接着,按照特定的顺序(例如,从上到下,再从下到上)将各栏中的字母重新组合成一行,形成密文。
以明文“THE LONGEST DAY MUST HAVE AN END”为例,如果选择两栏进行加密,过程如下:
重新组合:将第二栏的字母放在第一栏的后面,得到密文
加密算法
代码说明
splitString 函数:
该函数将输入字符串按照指定的步长(key)进行分割,生成一个二维列表。 如果字符串长度不能被步长整除,则在字符串末尾添加空格,以确保每个子串的长度一致。
主程序:
从用户输入获取要加密的信息和步长(key)。 去除输入信息中的空格。 调用 splitString函数将字符串分割成二维列表。遍历二维列表,按列取出字符,拼接成最终的密文。 输出加密后的密文。
使用示例
解密原理
解密是加密的逆过程。已知密文和栏数,解密者可以按照相反的顺序将密文重新排列成多栏,然后再将各栏的字母按照原始的顺序合并成明文。
例如,对于上述密文“TEOGSDYUTAENN HLNETAMSHVAED”,已知为两栏加密,解密过程如下:
重新组合:按照上下上下的顺序将两行字母合并成一行,得到明文“THE LONGEST DAY MUST HAVE AN END”。
解密算法
主要改动点:
函数和变量命名:将函数名和变量名改为符合 Python 命名规范的形式(使用小写字母和下划线)。 注释:增加了一些注释以提高代码的可读性。 代码结构:调整了代码结构,使其更加清晰和易读。 输入处理:去掉了不必要的 str()转换,因为input()函数已经返回字符串类型。
仿射密码
结合了凯撒密码和乘法密码的特点,通过线性变换进行加密。
加解密函数
仿射密码具有可逆性的条件是:
gcd(k1, n)=1. 当 k1=1 时,仿射密码变为加法密码,当 k2=0 时,仿射密码变为乘法密码。
仿射密码中的密钥空间的大小为nφ(n),当 n 为 26 字母,φ(n)=12,因此仿射密码的密钥空间为12×26 = 312。
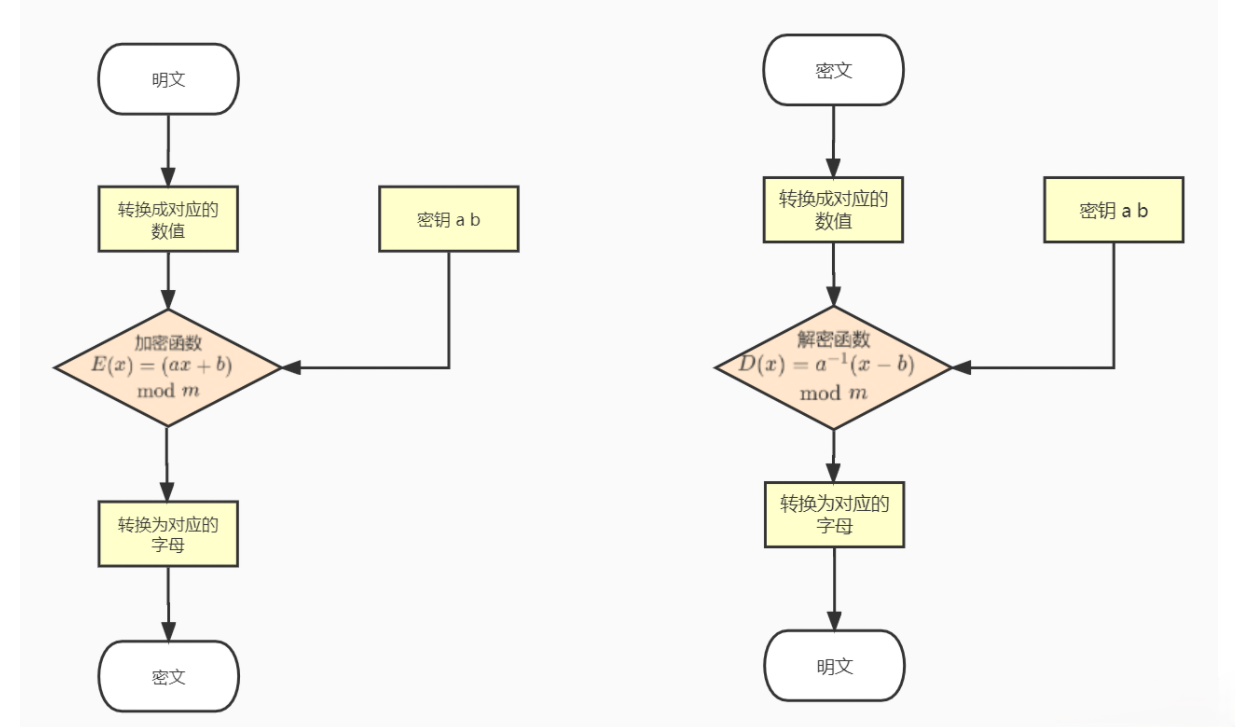
加密
设密钥 K= (7, 3), 用仿射密码加密明文 hot。 三个字母对应的数值是 7、14 和 19。
分别加密如下:
三个密文数值为 0、23 和 6,对应的密文是 AXG。
解密
先来引入一个定义. 大家知道, 好多东西都有逆, 大家读小学时都知道,两个数相乘乘积为 1,则互为倒数, 其实是最简单的逆. 后来, 我们到了高中, 我们学习了逆函数; 到了大学, 我们学习线性代数,知道两个矩阵的乘积为单位矩阵的话,则这两个矩阵互为逆矩阵. 现在我跟大家介绍另一种逆. 叫模逆. 其实很好理解的, 如下: 若 a,b 两数的乘积对正整数 n 取模的结果为 1. 则称 a,b 互为另外一个的模逆. 比如:
37 = 21; 21 % 20 = 1 ; 所以 3,7 互为 20 的 模逆. 93 = 27; 27 % 26 = 1 ; 所以 9,3 互为 26 的 模逆. 如何标记?
利用 java 代码求模逆
利用 c++实现加解密
摩斯电码
通过点和划的不同组合来表示不同的字母和数字,主要用于电报通信。
摩尔斯电码(Morse code)也被称作摩斯密码,是一种时通时断的信号代码,通过不同的排列顺序来表达不同的英文字母、数字和标点符号。它发明于 1837 年,是一种早期的数字化通信形式。不同于现代化的数字通讯,摩尔斯电码只使用零和一两种状态的二进制代码,它的代码包括五种:短促的点信号“・”,保持一定时间的长信号“—”,表示点和划之间的停顿、每个词之间中等的停顿,以及句子之间长的停顿。
编码表
摩尔斯电码的一个特点就是所有的字母并不是等长的,我们可以从它的编码表中直观的看到。
 其实换一种方式来看这张编码表,会更好理解,因为这其实就是一棵霍夫曼树(Huffman Tree)。
其实换一种方式来看这张编码表,会更好理解,因为这其实就是一棵霍夫曼树(Huffman Tree)。
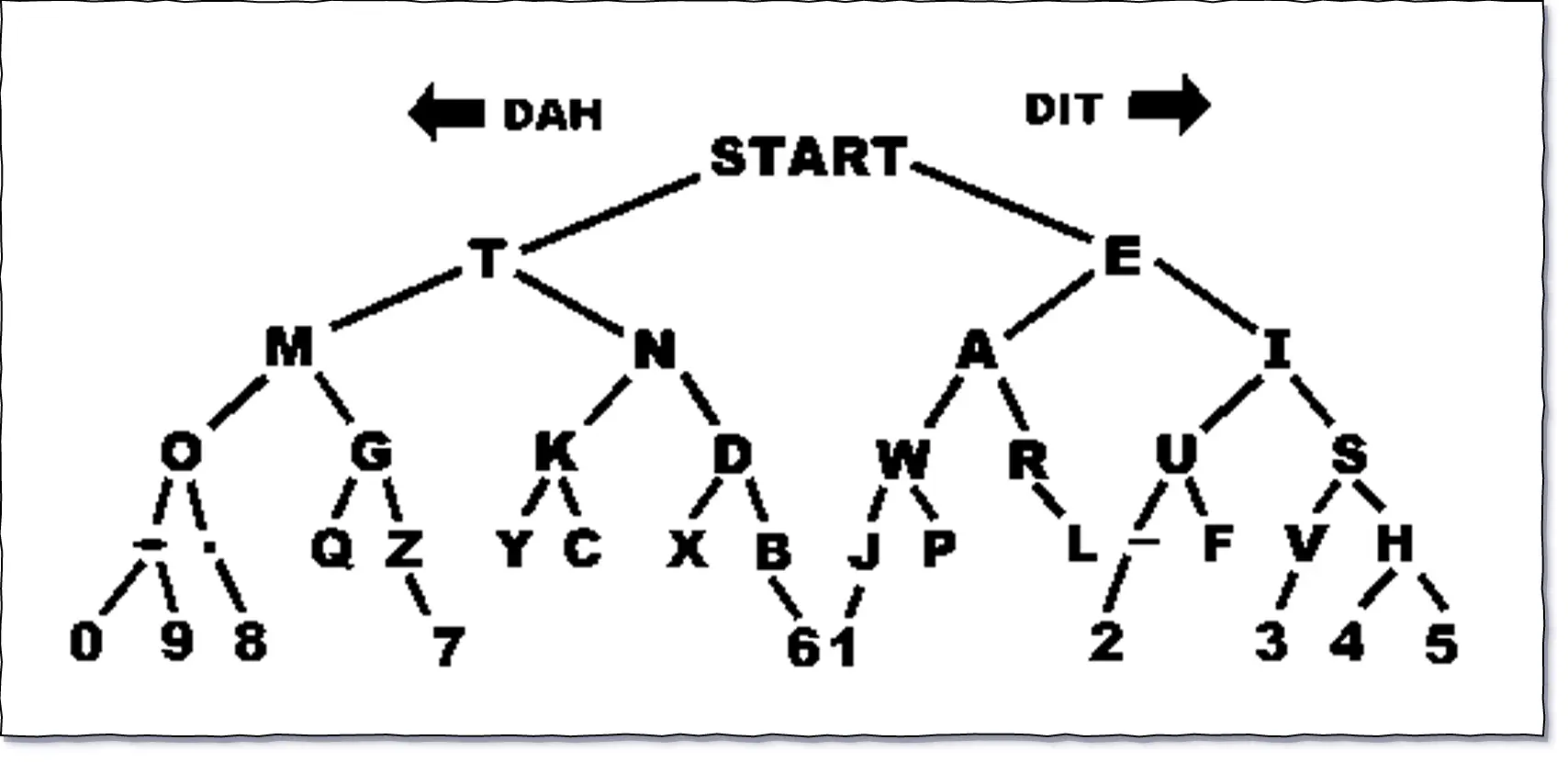
结构组成
首先,我们问一个问题:摩尔斯电码,只包含点和中横线吗?
如果不仔细翻看资料,可能大部分人会认为摩尔斯电码是由 · 和 - 组成的,也就是我们常说的「点」和「中横线」,也可以写作dot 和 dash。
但是实际上,无论从什么角度来考虑,摩尔斯电码都不止包含这两个元素。
先来简单测试一下,如果我们只使用· 和 - 来编码 hello world会怎样:
 这好像和我们经常见到的不一样,难道不应该是这样的么?
这好像和我们经常见到的不一样,难道不应该是这样的么?
 另一个角度,我们知道 - 实际上是三倍长度的 ·。
另一个角度,我们知道 - 实际上是三倍长度的 ·。
那么,假如我发送了 ... ,我要发送的是 S 呢?还是 EEE 呢?还是 T 呢?
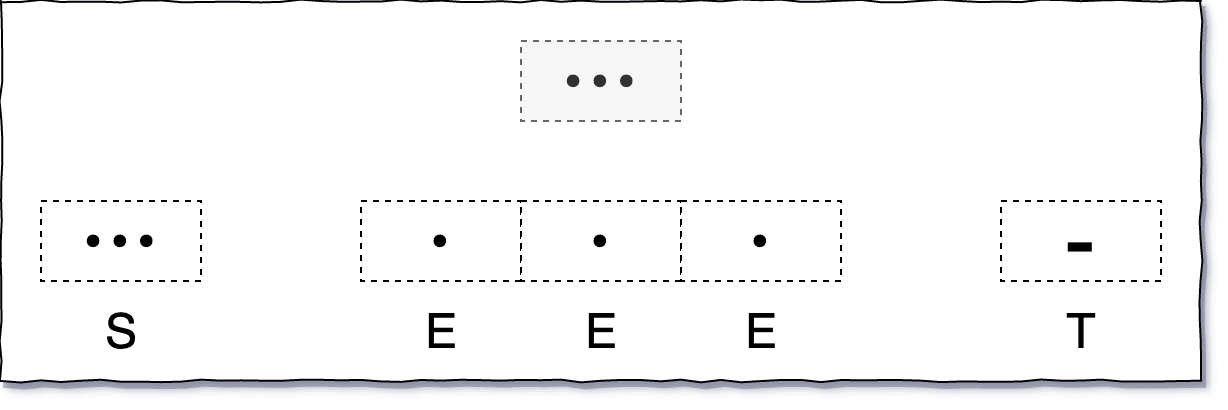 难道分隔符被隐藏了?
难道分隔符被隐藏了?
此时我们似乎发现了一个隐藏的字符,那就是空格,或者叫分隔符。
我们都知道,使用摩尔斯电码发送电报的时候需要使用「电键」,而电键的基础原理其实就是控制电路在「通」「断」两种状态间切换,通过按下时长的长短来区分「点」「中横线」。
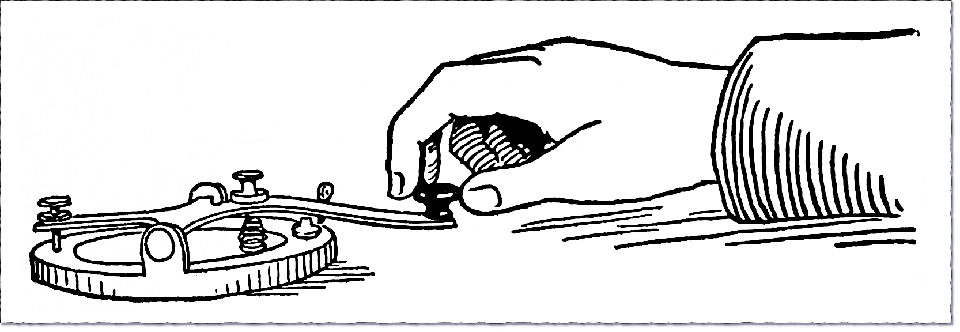 也就是说,「点」与「点」之间,「字符」与「字符」之前,其实是通过间隔来进行分隔的。
也就是说,「点」与「点」之间,「字符」与「字符」之前,其实是通过间隔来进行分隔的。
我们假定一个「点」的时长为一个单位长度 T,那么「中横线」的时长就是 3T。
同一个字符内部的「点」「中横线」间的间隔也是 T,字符间的间隔是 3T,而单词间的间隔则是 7T。
此处我们选择两个字符 O 和 R 作为示意,在发报的过程中,电路的通断情况其实是下面这样的:
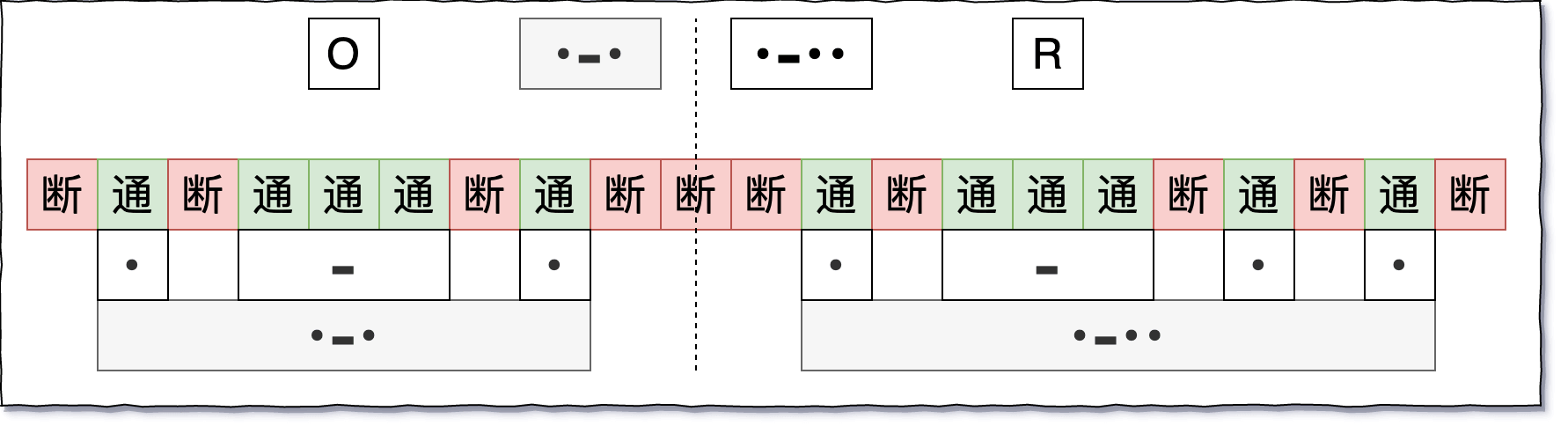 这样,我们就可以用简单的「通」「断」来表示出摩尔斯电码了。
这样,我们就可以用简单的「通」「断」来表示出摩尔斯电码了。
二进制
其实看到上面的示意图就会发现,其实电路状态的「通」「断」,完全可以理解为二进制的 1 和 0,而摩尔斯电码的基本组成结构,也可以理解为只有「通」「断」。
当然,我们也可以理解按常见的方式去理解它的结构,只是这下我们知道它背后的底层内容了。
其实换一个角度也很容易想明白,基于电路通断的摩尔斯电码,不论上层怎么定义,都不可能绕开底层只有两种状态这件事。
传输效率
从上面的示意图中,其实我们还能发现另一个问题,摩尔斯电码的效率并不高。
发送 OR 两个字符,总共用了 21T 的时长,操作手按下电键 7 次,这个效率用作信息传递不免让人觉得有些焦躁。
于是,就有了各种提升摩尔斯电码效率的操作。
信息压缩
需要说明的是,需要被压缩的并不是摩尔斯电码,而是英文单词。
正如许多人使用 tks 来代指 thanks ,BTW 来代指 by the way 一样,英文世界里也存在着大量的对常用词汇的缩写。一百多年前的前辈们,也是对它进行了充分的利用。
这些缩写分为两类,一类是简单的拼接字符,形成短词,相当于单词缩写。
另一类则是直接造了新的字符出来,称为特殊符号(统一符号)。
斯巴达密码棒
通过将字母写在缠绕在圆木棍上的羊皮纸上,然后重新展开来读取加密信息。
在密码学里,密码棒是个可使的传递讯息字母顺序改变的工具,由一条加工过、且有夹带讯息的皮革绕在一个木棒所组成。在古希腊,文书记载着斯巴达人用此于军事上的讯息传递。
密码接受者需使用一个相同尺寸、让他将密码条绕在上面解读的棒子。快速且不容易解读错误的优点,使它在战场上大受欢迎。 但是它很容易就被破解了。
加密
假设那棒可写下四个字母使之围绕成圆圈且 5 个字母可连成一线。
解密
解密的方法其实就是将编码方法反过来:
波利比奥斯密码
使用一个 5x5 的方阵来加密字母,属于多表代换密码。 例:
在这个方阵中,每个字母都被分配了两个数字,第一个数字表示行号,第二个数字表示列号。例如:
以此类推,直到 Z 对应 55。
加密
文本准备:首先,将原始文本中的所有字母转换为大写,因为方阵通常只包括大写字母。如果文本中包含数字或特殊字符,它们需要被特别处理或排除。 字母转换:然后,将每个字母转换为对应的两个数字。例如,如果文本是 "HELLO",则转换为 "13 22 12 12 15"。 密文生成:这些数字对就是密文,可以安全地传输或存储。
解密
接收密文:接收到密文后,需要将其转换回原始的字母。
数字转换:根据方阵,将每个数字对转换回对应的字母。例如,如果收到的密文是 "13 22 12 12 15",则转换回 "HELLO"。
特点和局限性
简单性:波利比奥斯方阵的加密和解密过程相对简单,易于理解和实现。
可视化:方阵提供了一种直观的方式来查看和记忆字母与数字的对应关系。
频率分析:尽管将字母转换为数字,但字母的频率模式仍然存在。如果攻击者知道语言的常用字母频率,他们可以对密文进行频率分析,尝试破解密码。
扩展性:波利比奥斯方阵可以扩展到更大的方阵,以包含更多的字符,例如小写字母、数字或特殊字符。
安全性:在现代密码学标准下,波利比奥斯方阵被认为是不安全的,因为它容易受到各种密码分析技术的攻击。
Playfair 密码
使用密钥控制生成矩阵,然后每两个字母为单位进行代换。
Playfair 密码是一种使用一个关键词方格来加密字符对的加密算法,是一种多表代换的对称加密技术。
它依据一个 5*5 的正方形组成的密码表来编写,密码表里排列有 25 个字母。如果一种语言字母超过 25 个,可以去掉使用频率最少的一个。如,法语一般去掉 w 或 k,德语则是把 i 和 j 合起来当成一个字母看待。英语中 z 使用最少,可以去掉它。可以很好的防御频率分析法的攻击。
同时 Playfair 密码对明文和密文有一定的要求:在加密之前首先需要整理明文,将明文中两个字母组成一组,如果两个字母相同则分成两组,在每组的后面加字母 X 或 Q。如果明文字母个数是奇数,在最后一个字母之后加字母 X 或 Q。密文的字母个数一定是偶数,任意两个同组的字母都不会相同。
加密
若 m1,m2 在同一行,对应密文 c1,c2 分别是紧靠 m1,m2 右端的字母。其中第一列被看做是最后一列的右方。
若 m1,m2 在同一列,对应密文 c1,c2 分别是紧靠 m1,m2 下方的字母。其中第一行被看做是最后一行的下方。
若 m1,m2 不在同一行,不在同一列,则 c1,c2 是由 m1,m2 确定的矩形的其他两角的字母(横向替换或者纵向替换)。
解密—解密就是加密的逆过程
若 c1,c2 在同一行,对应明文 m1,m2 分别是紧靠 c1,c2 左端的字母。其中第一列被看做是最后一列的右方。
若 c1,c2 在同一列,对应明文 m1,m2 分别是紧靠 c1,c2 上方的字母。其中第一行被看做是最后一行的下方。
若 c1,c2 不在同一行,不在同一列,则 m1,m2 是由 c1,c2 确定的矩形的其他两角的字母(横向替换或者纵向替换)。
c++源码加解密实现
培根密码
加密时,明文中的每个字母都会转换成 5 个为一组由 a 和 b 组成的英文字母。
培根密码,也称为倍康尼密码,是由英格兰哲学家、政治家、作家、科学家弗朗西斯·培根发明的一种隐写术其原理是通过使用两种不同长度的序列来代表不同的字母,从而将加密信息隐藏在普通文本中。
培根密码的加密原理
准备明文:首先,准备一段需要加密的明文。 转换为序列:将明文中的每个字母转换为由五个字母组成的序列。例如,字母“A”可能被转换为“AAAAA”,字母“B”可能被转换为“AABAB”等。 应用隐写术:使用两种不同的字体或样式(如大写和小写,正体和斜体)来区分这些序列。例如,可以用粗体表示序列中的“B”,用正常字体表示序列中的“A”。 生成密文:将转换后的序列按照原文的顺序排列,形成密文。
两种加密方式
1、第一种方式:
2、第二种方式:
培根密码的解密原理
识别隐写术:首先识别出密文中所使用的两种不同字体或样式。 分割序列:将密文按照五个字母一组进行分割,得到一系列的序列。 对照解密表:根据预先准备的解密表,将每个序列转换回对应的字母。例如,序列“AAAAA”对应字母“A”,“AABAB”对应字母“B”。 还原明文:将解密后的字母按照原来的顺序排列,得到原始的明文。
基于python加解密源码
猪圈密码
一种以格子为基础的简单替代密码,一一对应的。
猪圈密码(Pigpen cipher,亦称朱高密码、共济会密码)是一种以格子为基础的简单替代式密码。即使使用符号,也不会影响密码分析,亦可用在其它替代式的方法。
一、密码符号与映射
构建猪圈图形 猪圈密码使用一种特定的图形,通常是由一些交叉的线条构成的格子形状,就像猪圈的围栏一样。例如,常见的基础图形是一个简单的几字形的交叉线条组合。
定义符号与字母的映射关系 在猪圈密码的图形中,不同的区域(由线条交叉划分而成)被赋予特定的符号,如点(·)或者小短线(-)等。 然后,这些符号按照一定的顺序(例如从左到右、从上到下等规则)与字母表中的字母建立一一对应的关系。比如,第一个符号可能对应字母“A”,第二个符号对应字母“B”,依此类推。
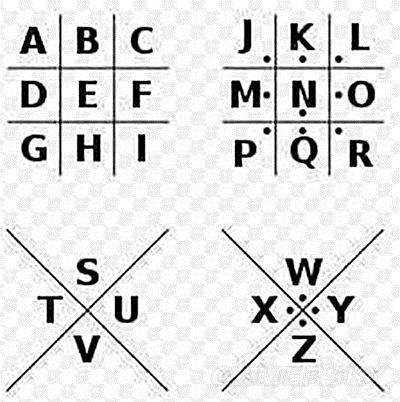

二、加密过程
分组明文 首先将明文按照一定的规则分组,通常是每组固定数量的字母(例如每组2 - 3个字母,具体取决于密码设置的复杂程度)。
转换为符号组合 根据预先设定的符号与字母的映射关系,将每组明文中的字母转换为对应的符号。如果某一组字母对应的符号组合超出了猪圈图形的基本符号范围,可能会涉及到一些特殊的转换规则,比如循环使用符号或者采用二级映射等。
绘制猪圈图形表示密文 最后,将得到的符号组合按照猪圈密码图形的规则绘制出来,形成类似猪圈形状的密文图形。这个图形就是加密后的结果,看起来只是一些线条和点的组合,对于不了解密码规则的人来说毫无意义。
三、解密过程
识别猪圈图形 解密者首先要识别出猪圈密码的图形结构,确定各个符号所在的位置和对应的规则。
符号还原为字母 根据已知的符号与字母的映射关系,将猪圈图形中的符号按照顺序还原为字母。
组合还原明文 把还原后的字母按照加密时的分组规则重新组合起来,就得到了原始的明文。
猪圈密码由于其图形化的特点,在早期被一些秘密组织(如共济会传闻中使用)用于保密通信,但随着密码学的发展,它已经被现代更强大的加密技术所取代,不过它仍然是密码学历史上一个有趣的研究对象。
基于python加解密源码
古典密码的应用场景
古典密码主要应用于军事和外交领域,用于保护机密信息。例如,凯撒密码曾被罗马帝国的恺撒大帝用于战争通信。
古典密码的局限性
尽管古典密码在历史上发挥了重要作用,但其安全性较低,容易被破解。例如,凯撒密码的密钥空间较小,容易受到频率分析等攻击方法的破解。
__EOF__

本文链接:https://www.cnblogs.com/leyinsec/p/18673777.html
关于博主:评论和私信会在第一时间回复。或者直接私信我。
版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
声援博主:如果您觉得文章对您有帮助,可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力!




【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 一个费力不讨好的项目,让我损失了近一半的绩效!
· 实操Deepseek接入个人知识库
· CSnakes vs Python.NET:高效嵌入与灵活互通的跨语言方案对比
· 【.NET】调用本地 Deepseek 模型
· Plotly.NET 一个为 .NET 打造的强大开源交互式图表库