深入理解并查集

并查集是一种树形结构，它是由并查集算法进行维护的。而并查集算法（Union-find-algorithm），顾名思义，它主要是由 “合并集合” 和 “查找集合”，”合并集合“是将两个连通的集合合并为一个集合，”查找集合“判断某个节点的代表节点，也就是根节点。

1. 并查集算法的应用场景

• 图的连通性，可以用来判断哪些节点是连通的。也可以知道一个图一共能被分成几个相互独立的块。

2. 算法简介

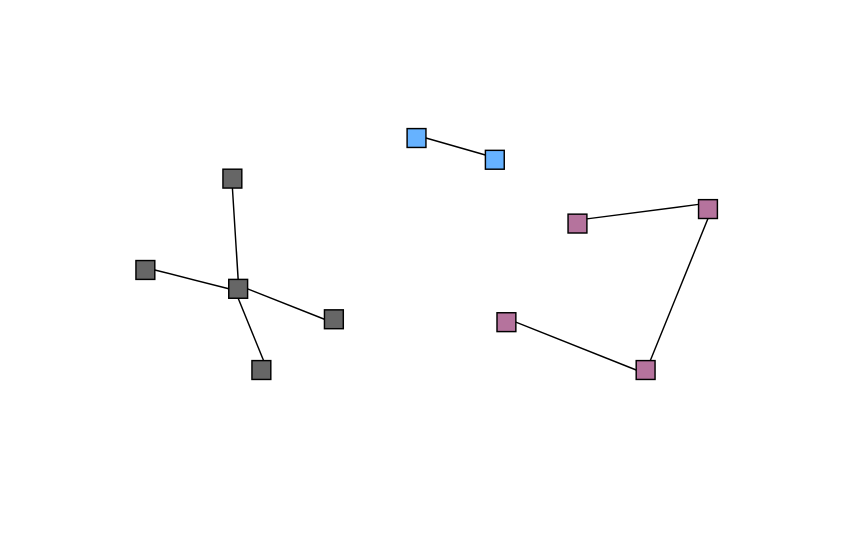
图的连通状态如上图所示，共分为三个集合，灰色、蓝色、粉色。在一个集合中任何两个点都是连通的。

如何判断两个点是否在同一集合中呢，我们可以组织一种树形结构，选择一个点当做根节点。要判断两个点是否在同一集合中，只需要分别对两个点向上寻找，一直找到根节点。如果根节点相同，那么连个点在同一集合中，两个点是连通的。

不同集合之间一定不能连通。

3.并查集算法

并查集算法是由一个数组和两个函数构成，数组 parents[ ] 其实就是树形结构的存储，记录了每个点的前导点是什么。函数 find 是查找， union 是合并。

3.1 查找算法

int len = 1000;
int pre[len];
int find(int c) {				// 函数返回 c 的根节点
    int r = c;
    while(parents[r] != r) {    // 返回根节点 r
        r = parents[r];
    }
    
    int i = c, j;
    while(i != r) {				// 压缩算法，将每个节点的父节点更新为根节点
        j = parents[i];
        parents[i] = r;			// 更新为根节点 r
        i = j;
    }
    return r;
}

查找过程如图所示：

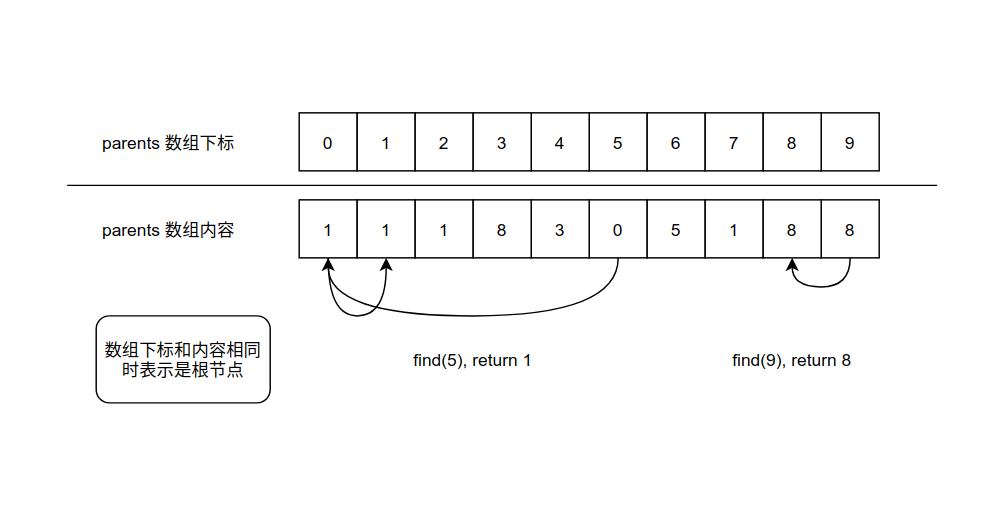
3.2 合并算法

void union(int node1, int node2) {		// 判断 node1 和 node2 是否连通，如果不连通那么将其所在分
    int root1 = find(node1);			// 支进行合并。
    int root2 = find(node2);
    if(root1 != root2) {
        parents[root1] = root2; 		// 合并：这里 root1 和 root2 的顺序可以不考虑
    }
}

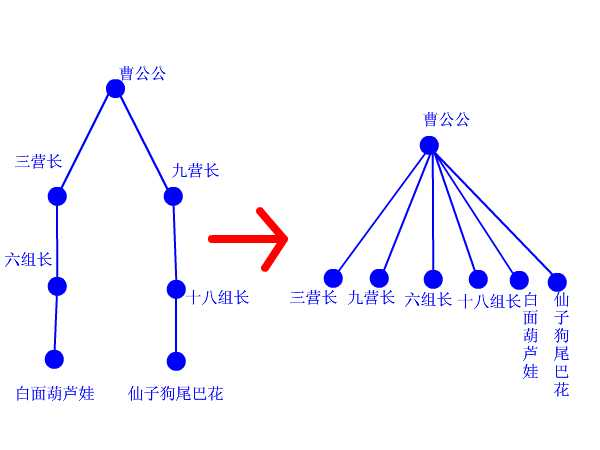
3.3 路径压缩

这里的压缩算法是为了提高查找效率，直接令每一个节点的父节点为根节点，那么每次要查找的时候只需要一次访问即可找到根节点。

4.例题

130. 被围绕的区域

难度中等208

给定一个二维的矩阵，包含 'X' 和 'O'（字母 O）。

找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例:

X X X X
X O O X
X X O X
X O X X

运行你的函数后，矩阵变为：

X X X X
X X X X
X X X X
X O X X

解释:

被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

并查集：

class UnionFind {
    public int[] parents;
    public UnionFind(int len) {
        this.parents = new int[len];
        for(int i = 0; i < len; i++) {
            parents[i] = i;
        }
    }

    public void union(int node1, int node2) {
        int root1 = find(node1);
        int root2 = find(node2);
        if(root1 != root2) {
            parents[root2] = root1;
        }
    }

    public int find(int node) {
        while (parents[node] != node) {
            parents[node] = parents[parents[node]];
            node = parents[node];
        }
        return node;
    }

    boolean isConnect(int node1, int node2) {
        return find(node1) == find(node2);
    }
}

将边界的 O 和 内部的 O 分成两个集合，然后对内部的 O 进行替换为 XX

public class Solution {
    // 并查集
    public int cols;
    public void solve(char[][] board) {
        if(board == null || board.length == 0) return;
        int rows = board.length;
        int cols = board[0].length;
        this.cols = cols;
        int RootNode = rows*cols;
        UnionFind uf = new UnionFind(rows*cols + 1);
        for(int i = 0; i < rows; i++) {
            for(int j = 0; j < cols; j++) {
                // 边界 ‘O’
                if(board[i][j] == 'O') {
                    if(i == 0 || j == 0 || i == rows - 1 || j == cols - 1) {
                        uf.union(getIndex(i, j), RootNode);
                    } else {
                        // 上下左右合并
                        if(i-1 >= 0 && board[i-1][j] == 'O') {
                            uf.union(getIndex(i, j), getIndex(i-1, j));
                        }
                        if(j-1 >= 0 && board[i][j-1] == 'O') {
                            uf.union(getIndex(i, j), getIndex(i, j-1));
                        }
                        if(i + 1 <= rows - 1 && board[i+1][j] == 'O') {
                            uf.union(getIndex(i, j), getIndex(i+1, j));
                        }
                        if(j+1 <= cols - 1 && board[i][j+1] == 'O') {
                            uf.union(getIndex(i, j), getIndex(i, j+1));
                        }
                    }
                }
            }
        }

        for(int i = 0; i < rows; i++) {
            for(int j = 0; j < cols; j++) {
                if(board[i][j] == 'O' && !uf.isConnect(getIndex(i, j), RootNode)) {
                    board[i][j]='X';
                }
            }
        }
    }

    public int getIndex(int i, int j) {
        return i*cols + j;
    }

}