前端小白的算法之路
时隔多日终于解决了埋在心头的一道难题,霎时云开雾散,今天把一路而来碰到的疑惑和心得都记录下来,也算是开启了自己探索算法的大门。
问题背景
曾经有一个年少轻狂的职场小白,在前端圈子里摸爬滚打将近两年,本计划在js的道路上越走越远,以至于每天沉浸在js红皮书里不能自拔,突然有一天脑抽想找leader比划两下,于是出现了下面的对话,小白:leader,您最近在干嘛?手里有需要亟待解决的难题吗?leader:咦,确实有哎,咱的项目随着业务的不断发展,日均PV也越来越多,公司的两台机器已经快满足不了需求,现在需要解决一下机器的问题。小白:那还不简单,就是多搞几台机器,四核换八核,可以并行处理就OK了。leader:小伙子想法很美好啊,钱从哪来?那我先问你个简单的问题[1],你写个算法出来。于是这个问题应用而生,小白也开始了苦苦的算法中。。。
问题阐述
假设一台双核处理器可以并行处理任务,它们的处理速度都为1k/s,每个任务均以k为单位,如[300, 600, 300, 500, 1000, 700, 300],且每个任务不能拆分必须由单独的核来执行,求一堆任务的最短时间算法?
(如果你对这个问题感兴趣或者觉得自己很NB,可以停下来试着写一下这个算法,不要偷看我的代码哈😃高手略过😂)
算法之路
看到这个问题,第一反应很简单,无非就是先排个序,然后看情况再分配任务,于是有了下面的第一版程序:
let arr = [300, 600, 300, 500, 1000, 700, 300];
function task(arr) {
let left = [];
let right = [];
let lefts = 0;
let rights = 0;
let flag = true; // 第一次累加最大值 第二次累加最小值 平分两组任务
// 平分两组任务
let newArr = arr.sort((a, b) => b - a);
if (flag) {
left.push(newArr[0]);
right.push(newArr[1]);
newArr = newArr.slice(2);
} else {
left.push(newArr[newArr.length - 1]);
right.push(newArr[newArr.length - 2]);
newArr = newArr.slice(0, newArr.length - 2);
}
// 开关循环 第一次加最大值 第二次加最小值 依次累加
flag = !flag;
// 两组任务分别之和
lefts = left.reduce((a, b) => a + b);
rights = right.reduce((a, b) => a + b);
// 只剩下一个任务或0个任务时,最终结果计算
if (newArr.length <= 1) {
if (newArr.length == 1) {
if ((lefts - rights) > newArr[0]) {
return lefts;
} else {
right.push(newArr[0]);
rights = right.reduce((a, b) => a + b);
return rights;
}
} else {
if (lefts < rights) {
return rights;
} else {
return lefts;
}
}
}
// 递归调用实现循环
return task(newArr);
};
alert("最短时间为:" + task(arr) + 's');
基本思路就是先把一堆任务排序,然后开始分配,第一次给第一台机子最大值,第二台机子次大值,第二次给第一台机子最小值,第二台机子次小值,依次递归调用累加,直至最后结束,如果是奇数个任务最后剩下一个任务的话,需要把这个任务分给时间较小的一组,最后返回一组时间较大的即是最终所需的最短时间。
显然这个程序是有问题的,于是开始了研究,多天之后依旧没有给出正确的答案,凭借一己之力显然不能解决,然后开始在segmentfault上提问,没想到很快就有人回复了,是NP-hard问题。近似算法参见partition problem。
看到回复后迫不及待的开始百度Google,竟然让我大吃一惊,2000年,美国克莱数学研究所公布了世界七大数学难题,又称千禧年大奖难题。其中P与NP问题被列为这七大世界难题之首,看到这大大激发了我对这一问题的研究热情,于是开始了NP问题的研究。
NP-hard,其中NP是指非确定性多项式(non-deterministic polynomial,缩写NP)。所谓的非确定性是指,可用一定数量的运算去解决多项式时间内可解决的问题。NP-hard问题通俗来说是其解的正确性能够被“很容易检查”的问题,这里“很容易检查”指的是存在一个多项式检查算法。相应的,若NP中所有问题到某一个问题是图灵可归约的,则该问题为NP困难问题。
旅行推销员问题就是最著名的NP问题之一,当然我要解决的这个问题(多线程多机调度问题)也属于NP问题之一,一般使用贪心算法来解决,于是我就开始了贪心算法之路。
算法描述
贪心算法:(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
思想: 贪心算法的基本思路是从问题的某一个初始解出发一步一步地进行,根据某个优化测度,每一步都要确保能获得局部最优解。每一步只考虑一个数据,他的选取应该满足局部优化的条件。若下一个数据和部分最优解连在一起不再是可行解时,就不把该数据添加到部分解中,直到把所有数据枚举完,或者不能再添加算法停止。
过程:
- 建立数学模型来描述问题;
- 把求解的问题分成若干个子问题;
- 对每一子问题求解,得到子问题的局部最优解;
- 把子问题的解局部最优解合成原来解问题的一个解。
解决思路
多线程问题主要是多个服务器可以并行处理多个任务,寻求处理所有任务的情况下,用掉最少时间的问题。因为任务并不局限于在某一个服务器上处理,而且任务不能拆分,所以还是要综合考虑怎么分配任务,属于多线程问题。
核心思路:(n代表任务,m代表机器)
- 将n个独立的任务按照时间从大到小排序;
- 如果n<=m,则需要的最短时间就是n个任务当中的最大时间;
- 如果n>m,则先给每个机器依次分配任务,第一次就分配了m个作业;
- 然后循环第一次分配的m个任务时间,选取处理时间最短的机器分配第m+1个任务;
- 依次循环所有机器所需时间,并选取最短时间的机器分配下一个任务;
- 最后比较返回最长时间的机子时间则为所需的最短时间。
实现过程:
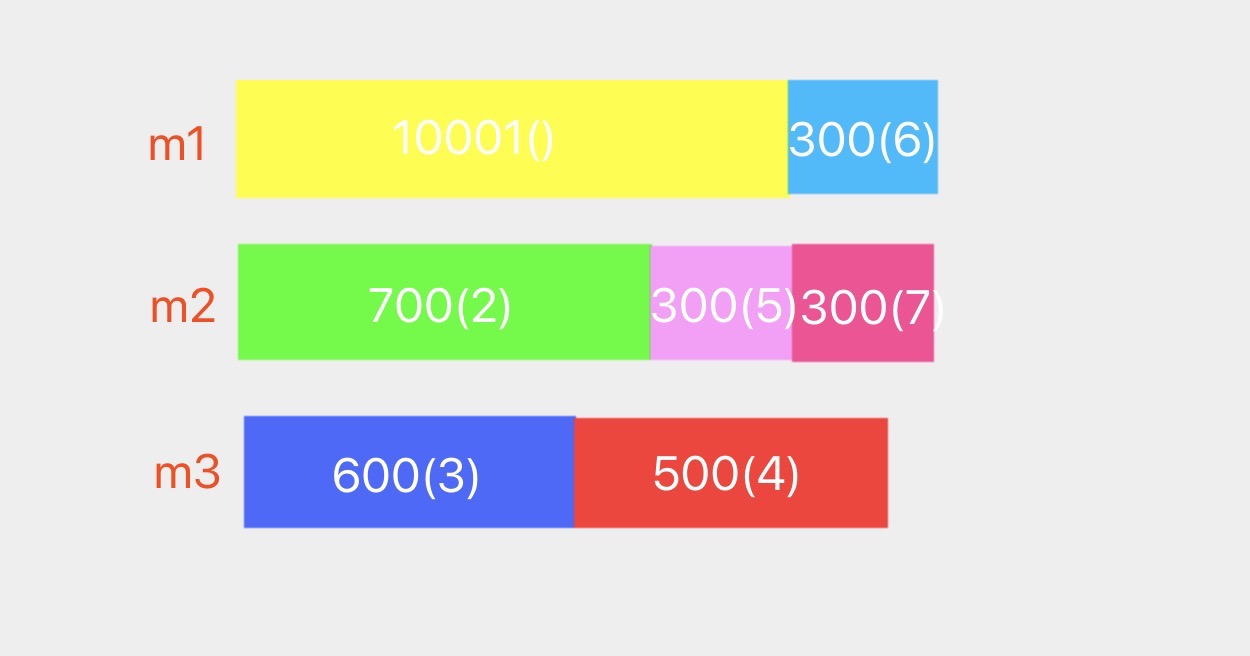
程序设计
第二版程序:
let arr = [700, 400, 300, 500, 100, 900];
function task(arr) {
// 1. 任务排序
let newArr = arr.sort((a, b) => b - a);
// 2. 两组各取最大值和次大值
let left = [newArr[0]];
let right = [newArr[1]];
newArr = newArr.slice(2);
// 3. 分别计算两组所用的时间
let lefts = newArr[0];
let rights = newArr[1];
// 4. 比较哪一组时间少就依次把下一个任务分给少的那组
newArr.forEach((item, index) => {
if (lefts < rights) {
left.push(item);
} else {
right.push(item);
}
// 分别计算每组所用的时间
lefts = left.reduce((a, b) => a + b);
rights = right.reduce((a, b) => a + b);
});
// 5. 返回较大值则是所用最短时间
return Math.max(lefts, rights);
};
alert("最短时间为:" + task(arr) + 's');
以上的第二版程序还是以最初的问题双核处理器(相当于两个机子)实现的,经测试正确通过,于是又拓展了多线程多机器的常见问题,就有了最终版的程序。
第三版程序:
let tasks = [300, 600, 300, 500, 1000, 700, 300];
function task(tasks, nums) {
// 1. 对任务进行从大到小排序
tasks = tasks.sort((a, b) => b - a);
// 2. 第一次给nums个机器分配前nums个任务
let machine = JSON.parse(JSON.stringify(Array(nums).fill([])));
tasks.forEach((item, index) => {
if(index < nums) {
machine[index].push(item);
}
});
// 3. 分别计算每个机器执行任务的时间
let times = Array(nums);
machine.forEach((item, index) => {
times[index] = item.reduce((a, b) => a + b);
});
// 4. 全部任务去掉第一次分配的nums个任务
tasks = tasks.slice(nums);
// 5. 比较哪台机器用的时间少就给哪台机器分配下一个任务
tasks.forEach((item, index) => {
// 给最短时间的机器分配任务
times.some((items, indexs) => {
if(items == Math.min(...times)) {
machine[indexs].push(item);
return true;
}
});
// 分别计算每台机器的执行时间
machine.forEach((items, indexs) => {
times[indexs] = items.reduce((a, b) => a + b);
});
});
// 6. 返回所有机器中时间最长的即是所有任务执行的最短时间
return Math.max(...times);
};
alert("最短输出时间为:" + task(tasks, 3) + 's');
哈哈,终于可以松口气了,这一路下来也是历尽艰辛,在此非常感谢清华大学的@萝卜的指点迷津,一语惊醒梦中人,让我找到了解法,虽然不是最优的算法,也让我醍醐灌顶,打开了探索算法的大门。以上代码是用JavaScript实现的(你可以用你熟悉的语言实现一下哈😃),其他语言也是一样的逻辑,所以做前端的千万不要在js的世界里妄自尊大,要站在CTO的角度放眼全局,尤其是多熟悉一些算法,这样的话编程思维更有逻辑性,解决问题能力更强,在公司的不可替代性也就更大了。
反思总结
- 算法是计算机科学领域最重要的基石之一,因为计算机语言和开发平台日新月异,但万变不离其宗的是最基础的算法和理论,比如数据结构、算法设计、编译原理、计算机操作系统和数据库原理等等。在“开复学生网”上,有位同学生动地把这些基础课程比喻为“内功”,把新的语言、技术、标准比拟为“外功”。整天赶时髦的人最后只懂得招式,没有功力,是不可能成为武林高手的。由此知道了算法的重要性,以后要多加学习。
- 善于向别人请教,计算机这个领域博大精深,自己不懂的还有很多很多,就比如这次脑子里就没有贪心算法这种思想,只能硬碰运气试答案,显然是浪费时间瞎折腾,遇到研究好久都没答案的问题一定要多加请教。
- 善于归纳总结,积少成多,厚积薄发。


