会员
周边
新闻
博问
闪存
众包
赞助商
Chat2DB
所有博客
当前博客
我的博客
我的园子
账号设置
会员中心
简洁模式
...
退出登录
注册
登录
lewisak
博客园
首页
新随笔
联系
订阅
管理
[置顶]
工具
摘要: 常用 latex 常用 emoji
阅读全文
posted @ 2025-12-28 18:17 LEWISAK
阅读(19)
评论(0)
推荐(0)
[置顶]
gxyz圣经
摘要: 建议改名战败 CG 合集。 已完成今日还有这里我必须严肃评价一下我们机房的状态了老师把A和B赶了出去说A和B学习习惯不好但实际情况是什么呢只有A和B从来不玩游戏还有没有来和zr联考的C和D我们把他和zr联考中公认的E进行一个对比心态C不在明显比E更差但是另外一个其实罢了两个人实力上也不比那个谁低啊说
阅读全文
posted @ 2025-11-07 16:20 LEWISAK
阅读(250)
评论(23)
推荐(1)
[置顶]
图床
摘要: 密码是瞎投右子树
阅读全文
posted @ 2025-10-31 16:31 LEWISAK
阅读(46)
评论(7)
推荐(0)
[置顶]
神笔trick
摘要: 记得定期看看把数值崩坏淘汰掉的删了🙄 密码不告诉你😜
阅读全文
posted @ 2025-07-29 16:08 LEWISAK
阅读(4)
评论(1)
推荐(0)
[置顶]
注意!
摘要: 可能会持续更。。。
阅读全文
posted @ 2025-05-07 08:21 LEWISAK
阅读(79)
评论(0)
推荐(0)
[置顶]
蠢梦合集
摘要: 2017.??.?? 包饺子了! 我可以和老师包饺子! 我和老师包了一会后,她说她要回她的班了。 好吧。 我醒了。 2017.??.?? 滑滑梯~ 滑到底部后,有陌生人给我洗脚。 2018.??.?? 沙漠上有怪物。 我在划沙板上战斗。 我到了集合地才知道怪物都是人。 我杀了人? 有人给我了幻觉。
阅读全文
posted @ 2025-04-29 10:04 LEWISAK
阅读(211)
评论(5)
推荐(2)
[置顶]
随机说话!?
摘要: 随机说话
阅读全文
posted @ 2025-02-10 14:01 LEWISAK
阅读(191)
评论(3)
推荐(1)
[置顶]
诸子百家的经典语录,一生至少读一遍!
摘要: 其实是唐话合集
阅读全文
posted @ 2024-08-10 16:47 LEWISAK
阅读(424)
评论(14)
推荐(2)
2026年2月9日
整体二分学习笔记
摘要: 1 算法简介 二分答案是一种常用的算法,而你可能有所不知的是,它还有一种冷门的递归写法: void BS(int l,int r,int pl,int pr){ if (l==r){ ans=l; return; } int mid=(l+r)>>1; int cnt=0,n1=0,n2=0; fo
阅读全文
posted @ 2026-02-09 20:43 LEWISAK
阅读(10)
评论(0)
推荐(0)
2026年2月6日
线段树综合学习笔记
摘要: 线段树技巧串烧速推🤩! 1 线段树分裂 1.1 算法介绍 让线段树能够像 FHQ-Treap 一样分裂! 由于这个东西确实不难理解所以直接看代码和注释吧: void split(int x,int &y,int k){//把 x 除前 k 小的部分分到 y 里 if(!x) return;//边界
阅读全文
posted @ 2026-02-06 16:08 LEWISAK
阅读(11)
评论(0)
推荐(0)
2026年1月17日
[CF603E] Pastoral Oddities 题解
摘要: 是。 不知道为啥这题想写详细点。 题意简述 有一个 \(n\) 个点的简单图,你需要动态加入 \(m\) 条边并在每一次加边后回答选边使得每个点的度数都为奇数时,最大边权的最小值,若无解输出 -1。 \(2\le n\le 10^5\),\(1\le m\le 3\times 10^5\)。 题解
阅读全文
posted @ 2026-01-17 12:34 LEWISAK
阅读(8)
评论(0)
推荐(0)
2026年1月2日
关于颜色段均摊的一种跨时代性新思路!
摘要: 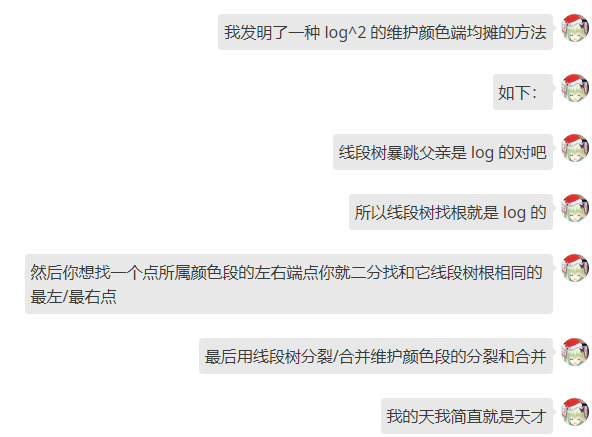 
阅读全文
posted @ 2026-01-02 19:20 LEWISAK
阅读(16)
评论(0)
推荐(0)
主席树学习笔记
摘要: 其实主席树我在 10000 年前就会了但这个知识点题单顺序非常靠后导致现在才写( 1 算法介绍 主席树是可持久化权值线段树的别称,但这个权不权值的已经没有人强调了,我也会混淆主席树和普通权值线段树的概念,毕竟主席树字少嘛🤔。 1.1 单点修改 先讲可持久化维护单点修改区间查询。 可持久化:指能够维
阅读全文
posted @ 2026-01-02 14:17 LEWISAK
阅读(16)
评论(0)
推荐(0)
2025年12月21日
拉格朗日插值总结
摘要: 1 算法介绍 众所周知的,\(n\) 个平面上的 \(x\) 坐标不同的点始终能用 \(n-1\) 次多项式来拟合。 假设拟合函数为 \(f\),给出点的坐标为 \((x_i,y_i)\),那么有: \[f(k)=\sum_{i=0}^{n}y_i\prod_{i\ne j}\frac{k-x_j}
阅读全文
posted @ 2025-12-21 16:01 LEWISAK
阅读(64)
评论(0)
推荐(1)
2025年12月9日
随机名字生成器
摘要: #include<bits/stdc++.h> using namespace std; namespace kong{bool st;} namespace zhu{ string fu[]={"q","w","r","t","y","p","s","d","f","g","h","j","k",
阅读全文
posted @ 2025-12-09 18:17 LEWISAK
阅读(20)
评论(0)
推荐(0)
2025年12月7日
吟诗一首
摘要: 朝起练武,雨如白绫\(^1\) 借因此由,幡然\(^2\)巡礼\(^3\) 至汐山\(^4\)中,四季各色 夏目盈绿\(^5\),冬月栞\(^6\)雪 秋打麦谷,春播芦花 又至户隐\(^7\),椎叶\(^8\)纷飞 花蕾窈娜,长路茉紫\(^9\) 屋中和奏,墨染溪流 如此宁宁\(^{10}\),何不
阅读全文
posted @ 2025-12-07 20:14 LEWISAK
阅读(80)
评论(3)
推荐(1)
2025年11月23日
惊天理论
摘要: 密码是游资处8字密语
阅读全文
posted @ 2025-11-23 21:43 LEWISAK
阅读(23)
评论(0)
推荐(0)
下一页
公告