H - Rescue the Princess ZOJ - 4097 (tarjan缩点+倍增lca)
题目链接:
H - Rescue the Princess
学习链接:
zoj4097 Rescue the Princess无向图缩点有重边+lca - lhc..._博客园
题目大意:
首先是T组测试样例,然后是n个点,m条双向边。然后给你u,v,w。问你v和w是否能够到达u,两个人走过的边不能有重复,否则这条边会被压塌。
具体思路:首先对能形成连通块的进行缩点,构成一个个的连通图。然后这样整个图就变成了一个森林,然后再根据染色后的连通块重新建图。
对于每一次的询问,先看这三个点是不是在同一个连通图里面,如果不是在一个连通图里面肯定是非法情况。
然后再就是讨论在同一个连通图里面的情况,通过讨论v和u的关系来表示出所有的情况。
情况1,lca(u,v)=u.
这种时候肯定是满足的,lca(u,v)=lca(u,w)=lca(v,w)=u.
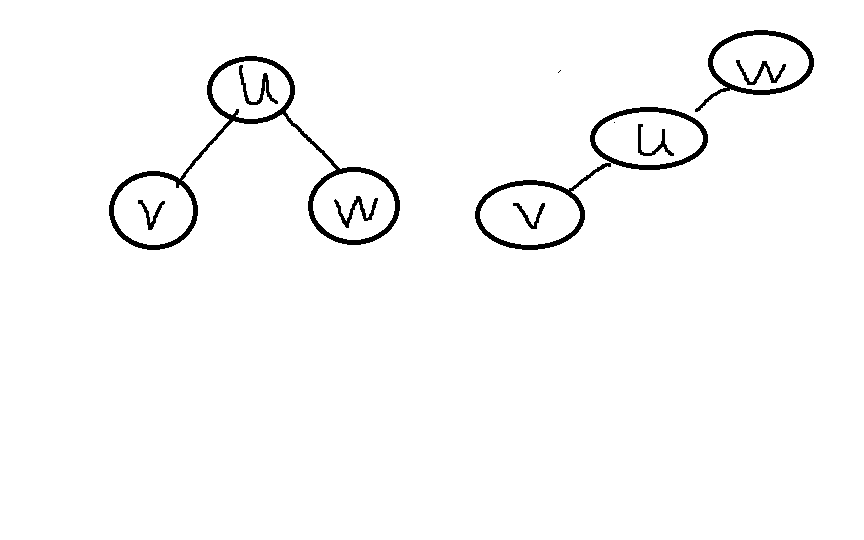
情况2,lca(u,v)=v.
情况3,lca(u,v)!=u&&lca(u,v)!=v.

讨论上述情况就可以了。
AC代码:
1 #include<bits/stdc++.h>
2 using namespace std;
3 # define ll long long
4 const int maxn =2e5+100;
5 int n,m,k,num,ordofblock,ordoftree;
6 vector<int>Edge1[maxn];
7 vector<int>Edge2[maxn];
8 int dfn[maxn],low[maxn];
9 int tree[maxn],block[maxn],vis[maxn];
10 int depth[maxn],father[maxn][25];
11 stack<int>q;
12 void init()
13 {
14 for(int i=0; i<=n; i++)
15 {
16 Edge1[i].clear();
17 Edge2[i].clear();
18 vis[i]=0;
19 dfn[i]=0;
20 low[i]=0;
21 tree[i]=0;
22 block[i]=0;
23 depth[i]=0;
24 for(int j=0;j<=20;j++)father[i][j]=0;
25 }
26 while(!q.empty())
27 q.pop();
28 num=0;
29 ordofblock=ordoftree=0;
30 }
31 void tarjan(int cur,int fa,int ord)
32 {
33 tree[cur]=ord;
34 low[cur]=dfn[cur]=++num;
35 q.push(cur);
36 int flag=0;
37 for(int i=0; i<Edge1[cur].size(); i++)
38 {
39 int to=Edge1[cur][i];
40 if(to==fa)
41 {
42 if(++flag<2)
43 continue;
44 }
45 if(!dfn[to])
46 {
47 tarjan(to,cur,ord);
48 low[cur]=min(low[cur],low[to]);
49 }
50 else if(!block[to])
51 {
52 low[cur]=min(low[cur],dfn[to]);
53 }
54 }
55 if(low[cur]==dfn[cur])
56 {
57 ordofblock++;
58 int tmp;
59 do
60 {
61 tmp=q.top();
62 q.pop();
63 block[tmp]=ordofblock;
64 }
65 while(tmp!=cur);
66 }
67 }
68 void dfs(int u,int root)
69 {
70 vis[u]=1;
71 depth[u]=depth[root]+1;
72 father[u][0]=root;
73 for(int i=1; (1<<i)<=depth[u]; i++)
74 {
75 father[u][i]=father[father[u][i-1]][i-1];
76 }
77 for(int i=0; i<Edge2[u].size(); i++)
78 {
79 int to=Edge2[u][i];
80 if(to==root)
81 continue;
82 dfs(to,u);
83 }
84 }
85 int lca(int t1,int t2)
86 {
87 if(depth[t1]>depth[t2])
88 swap(t1,t2);
89 for(int i=20; i>=0; i--)
90 {
91 if(depth[t1]<=depth[t2]-(1<<i))
92 {
93 t2=father[t2][i];
94 }
95 }
96 if(t1==t2)
97 return t1;
98 for(int i=20; i>=0; i--)
99 {
100 if(father[t1][i]!=father[t2][i])
101 {
102 t1=father[t1][i];
103 t2=father[t2][i];
104 }
105 }
106 return father[t1][0];
107 }
108 int main()
109 {
110 int T;
111 scanf("%d",&T);
112 while(T--)
113 {
114 scanf("%d %d %d",&n,&m,&k);
115 init();
116 int st,ed;
117 for(int i=1; i<=m; i++)
118 {
119 scanf("%d %d",&st,&ed);
120 Edge1[st].push_back(ed);
121 Edge1[ed].push_back(st);
122 }
123 for(int i=1; i<=n; i++)
124 {
125 if(!dfn[i])
126 {
127 ordoftree++;
128 tarjan(i,0,ordoftree);
129 }
130 }
131 for(int i=1; i<=n; i++)
132 {
133 for(int j=0; j<Edge1[i].size(); j++)
134 {
135 int to=Edge1[i][j];
136 if(block[i]!=block[to])
137 {
138 Edge2[block[i]].push_back(block[to]);
139 }
140 }
141 }
142 for(int i=1; i<=ordofblock; i++)
143 {
144 if(!vis[i])
145 dfs(i,i);
146 }
147 int u,v,w;
148 for(int i=1; i<=k; i++)
149 {
150 scanf("%d %d %d",&u,&v,&w);
151 if(tree[u]!=tree[v]||tree[u]!=tree[w]||tree[v]!=tree[w])
152 {
153 printf("No\n");
154 continue;
155 }
156 int flag=1;
157 u=block[u],v=block[v],w=block[w];
158 int uv=lca(u,v);
159 int uw=lca(u,w);
160 int vw=lca(v,w);
161 if(uv==u){
162 if(uw==u&&vw==u)flag=1;
163 else if(uw!=u)flag=1;
164 else flag=0;
165 }
166 else if(uv==v){
167 if(uw==u)flag=1;
168 else flag=0;
169 }
170 else {
171 if(uw!=u)flag=0;
172 }
173 if(flag)
174 printf("Yes\n");
175 else
176 printf("No\n");
177 }
178 }
179 return 0;
180 }


