容斥原理&&莫比乌斯专题
具体思路:如果是求n中,为平方数的有多少个,那么答案肯定是sqrt(n),同理,如果是三次根号的话,那么答案肯定是n的三分之一次方。然后继续按照这个思路来,对于1e18次方的数,最多就是2的64次方,也就是说我们最多枚举大小不超过63的素数就可以了,然后还需要考虑一种情况,比如说6的时候,被素数2算了一遍,然后又被素数3算了一遍,这个地方会有重复的计算,又因为2^(3*5*7)已经超过2的60次方了,所以我们只需要考虑三部分就可以了。
AC代码(1):
1 #include <iostream> 2 #include <string> 3 #include <deque> 4 #include <stack> 5 #include<cmath> 6 #include <algorithm> 7 #include<cstring> 8 #include<stdio.h> 9 #include<map> 10 using namespace std; 11 # define ll long long 12 # define inf 0x3f3f3f3f 13 # define ll_inf 1ll<<60 14 const int maxn = 1e6+100; 15 ll prim[]= {2,3,5,7,11,13,17,19,23,29,31,37,41,43,47,53,59,61}; 16 ll cal(ll t) 17 { 18 ll sum=1; 19 for(int i=0;; i++) 20 { 21 ll tmp=pow(t,1.0/(prim[i]*1.0)); 22 if(tmp<2) 23 break; 24 sum+=tmp-1; 25 for(int j=i+1;; j++) 26 { 27 tmp=pow(t,1.0/(prim[i]*prim[j]*1.0)); 28 if(tmp<2) 29 break; 30 sum-=tmp-1; 31 for(int k=j+1;; k++) 32 { 33 tmp=pow(t,1.0/(prim[i]*prim[j]*prim[k]*1.0)); 34 if(tmp<2) 35 break; 36 sum+=tmp-1; 37 } 38 } 39 } 40 return sum; 41 } 42 int main() 43 { 44 ll tmp; 45 while(cin>>tmp) 46 { 47 cout<<cal(tmp)<<endl; 48 } 49 return 0; 50 }
AC代码(2):
我们可以利用莫比乌斯系数进行简化计算,在上一个版本中,我们是按照奇加偶减的原则来进行的,同样这个计算的过程可以通过莫比乌斯中的mu函数来直接算出,每次相乘的系数是-mu[i]。
1 #include <iostream> 2 #include <string> 3 #include <deque> 4 #include <stack> 5 #include<cmath> 6 #include <algorithm> 7 #include<cstring> 8 #include<stdio.h> 9 #include<map> 10 using namespace std; 11 # define ll long long 12 # define inf 0x3f3f3f3f 13 # define ll_inf 1ll<<60 14 const int maxn = 100+100; 15 ll mu[maxn*100],prim[maxn*100],check[maxn*100]; 16 int tot=0; 17 void getmu() 18 { 19 mu[1]=1; 20 for(int i=2; i<maxn; i++) 21 { 22 // cout<<i<<endl; 23 if(!check[i]) 24 { 25 prim[tot++]=i; 26 mu[i]=-1; 27 } 28 for(int j=0; j<tot; j++) 29 { 30 // cout<<i<<endl; 31 if(prim[j]>maxn/i) 32 { 33 break; 34 } 35 check[i*prim[j]]=1; 36 if(i%prim[j]==0) 37 { 38 mu[i*prim[j]]=0; 39 break; 40 } 41 else 42 { 43 mu[i*prim[j]]=-mu[i]; 44 } 45 } 46 } 47 // cout<<1<<endl; 48 } 49 int main() 50 { 51 getmu(); 52 ll tmp; 53 while(cin>>tmp) 54 { 55 ll sum=1; 56 for(ll i=2; i<=64; i++) 57 { 58 sum-=mu[i]*(ll)(pow(tmp*1.0,1.0/i)-1); 59 } 60 cout<<sum<<endl; 61 } 62 return 0; 63 }
B题:
题目链接:
B - How many integers can you find
题目大意:输入n,m.然后再输入m个数,问你1-(n-1)中,是这些数中任意个倍数的有多少?
具体思路:我们可以运用容斥的原理,最终答案等于sum=(能被一个数整除)-(能被两个数整除)+(能被三个数整除)-------.然后按照这个思路,我们运用二进制枚举直接暴力就可以了。 (int会爆掉)
AC代码:
1 #include<iostream> 2 #include<stack> 3 #include<iomanip> 4 #include<cstring> 5 #include<string> 6 #include<cmath> 7 #include<algorithm> 8 #include<stdio.h> 9 using namespace std; 10 # define int long long 11 const int maxn = 100+10; 12 int a[maxn]; 13 int gcd(int a,int b){ 14 if(a<b)swap(a,b); 15 return a%b==0?b:gcd(b,a%b); 16 } 17 int lcm(int a,int b) 18 { 19 return a*b/gcd(a,b); 20 } 21 int cal(int n,int t) 22 { 23 int ans=0; 24 int maxstate=(1<<t)-1; 25 for(int i=1; i<=maxstate; i++) 26 { 27 int ind=0; 28 int tmp=1; 29 for(int j=0; j<=t; j++) 30 { 31 if((1<<j)&i) 32 { 33 ind++; 34 tmp=lcm(tmp,a[j+1]); 35 } 36 } 37 ans-=mu[tmp]*(n/tmp);//其实这个地方也可以直接通过一个莫比乌斯中的mu函数求,但是这样的话mu函数就需要求的比较大,所以对于这个题还是建议下面这个方法,按照容斥原理。 38 if(ind&1) 39 { 40 ans+=n/tmp; 41 } 42 else 43 ans-=n/tmp; 44 } 45 return ans; 46 } 47 signed main() 48 { 49 int n,m; 50 while(cin>>n>>m) 51 { 52 int tot=0; 53 int tmp; 54 n--; 55 for(int i=1; i<=m; i++) 56 { 57 cin>>tmp; 58 if(!tmp) 59 continue; 60 a[++tot]=tmp; 61 } 62 int ans=cal(n,tot); 63 cout<<ans<<endl; 64 } 65 // return 0; 66 } 67 //ll mu[maxn+100],prim[maxn+100],check[maxn+100]; 68 //void getmu() 69 //{ 70 // int tot=0; 71 // mu[1]=1; 72 // for(int i=2; i<maxn; i++) 73 // { 74 // if(!check[i]) 75 // { 76 // prim[tot++]=i; 77 // mu[i]=-1; 78 // } 79 // for(int j=0; j<tot; j++) 80 // { 81 // if(prim[j]>maxn/i) 82 // { 83 // break; 84 // } 85 // check[i*prim[j]]=1; 86 // if(i%prim[j]==0) 87 // { 88 // mu[i*prim[j]] 89 // =0; 90 // break; 91 // } 92 // else 93 // { 94 // mu[i*prim[j]]=-mu[i]; 95 // } 96 // } 97 // } 98 //} 99 //int main() 100 //{ 101 // getmu(); 102 // ll n,m; 103 // while(~scanf("%lld %lld",&n,&m)) 104 // { 105 // ll minn=1ll<<60,maxx=0; 106 // ll tmp=0; 107 // n--; 108 // for(int i=1; i<=m; i++) 109 // { 110 // scanf("%lld",&tmp); 111 // maxx=max(maxx,tmp); 112 // minn=min(minn,tmp); 113 // } 114 // ll sum=1; 115 // for(int i=minn; i<=maxx; i++) 116 // { 117 // sum-=mu[i]*(n/i); 118 // } 119 // cout<<sum<<endl; 120 // printf("%lldn") 121 // } 122 //}
C题:
C - Visible Trees
题目大意:给你一个n*m的图,你站在(0.0)这个点上,这个田地上从)(1,1)这个点开始有树,如果一个树和另外树在一条一个直线,这个时候后面那棵树就会看不到,然后问你这个人能看到多少树?
具体思路:首先来分析一波,如果一个树能被这个人看到,也就是说不会有别的树挡住当前这棵树,再分析到这棵树的坐标,也就说这个树的坐标不会被分解,也就说这个树的坐标x和y互素,分析到这里就可以了。我们只需要判断给定的(x,y),(1,x)和(1,y)这段区间互素的数有多少就可以了。莫比乌斯反演、、
计算过程:
然后对于当前这个题,选择(1,b),(1,d) 中满足gcd(x,y)==1的对数,(1<=x<=b),(1<=y<=d) .
也就是说 gcd(x,y)==1满足的对数.
然后再开始分析一波:
我们令f(k)为满足(a,b),(c,d)中的gcd为1的对数.然后F(1)就是满足(a,b),(c,d)中的gcd为k的倍数的对数.
F(k)就等于(b/k)*(d/k).
f(1)= 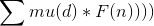
AC代码:
1 #include<iostream> 2 #include<stack> 3 #include<iomanip> 4 #include<cstring> 5 #include<string> 6 #include<cmath> 7 #include<algorithm> 8 #include<stdio.h> 9 using namespace std; 10 const int maxn = 100000+100; 11 # define int long long 12 int a[maxn]; 13 int mu[maxn+100],prim[maxn+100],check[maxn+100]; 14 void getmu() 15 { 16 int tot=0; 17 mu[1]=1; 18 for(int i=2; i<maxn; i++) 19 { 20 if(!check[i]) 21 { 22 prim[tot++]=i; 23 mu[i]=-1; 24 } 25 for(int j=0; j<tot; j++) 26 { 27 if(prim[j]>maxn/i) 28 { 29 break; 30 } 31 check[i*prim[j]]=1; 32 if(i%prim[j]==0) 33 { 34 mu[i*prim[j]] 35 =0; 36 break; 37 } 38 else 39 { 40 mu[i*prim[j]]=-mu[i]; 41 } 42 } 43 } 44 } 45 signed main() 46 { 47 getmu(); 48 int T; 49 int n,m; 50 cin>>T; 51 while(T--) 52 { 53 cin>>n>>m; 54 int sum=0; 55 int minn=min(n,m); 56 for(int i=1; i<=minn; i++) 57 { 58 sum+=mu[i]*(n/i)*(m/i); 59 } 60 cout<<sum<<endl; 61 } 62 return 0; 63 } 64 D题: 65 66 #include<iostream> 67 #include<stack> 68 #include<iomanip> 69 #include<cstring> 70 #include<string> 71 #include<cmath> 72 #include<algorithm> 73 #include<stdio.h> 74 using namespace std; 75 const int maxn = 1e6+100; 76 # define ll long long 77 ll a[maxn]; 78 ll mu[maxn+100],prim[maxn+100],check[maxn+100]; 79 void getmu() 80 { 81 int tot=0; 82 mu[1]=1; 83 for(int i=2; i<maxn; i++) 84 { 85 if(!check[i]) 86 { 87 prim[tot++]=i; 88 mu[i]=-1; 89 } 90 for(int j=0; j<tot; j++) 91 { 92 if(prim[j]>maxn/i) 93 { 94 break; 95 } 96 check[i*prim[j]]=1; 97 if(i%prim[j]==0) 98 { 99 mu[i*prim[j]] 100 =0; 101 break; 102 } 103 else 104 { 105 mu[i*prim[j]]=-mu[i]; 106 } 107 } 108 } 109 } 110 int main() 111 { 112 getmu(); 113 int T; 114 cin>>T; 115 int Case=0; 116 while(T--) 117 { 118 ll x1,y1,x2,y2; 119 cin>>x1>>y1>>x2>>y2; 120 ll k; 121 cin>>k; 122 if(k==0){ 123 printf("Case %d: %lld\n",++Case,0); 124 } 125 else { 126 127 y1/=k; 128 y2/=k; 129 ll sum1=0,sum2=0; 130 ll minn=min(y1,y2); 131 for(int i=1; i<=minn; i++) 132 { 133 sum1+=mu[i]*(y1/i)*(y2/i); 134 sum2+=mu[i]*(minn/i)*(minn/i); 135 } 136 printf("Case %d: %lld\n",++Case,sum1-sum2/2); 137 } 138 } 139 return 0; 140 } 141

