D. GCD Counting(树上dp)
题目链接:http://codeforces.com/contest/1101/problem/D
题目大意:给你n个点,每个点都有权值,然后给你边的关系,问你树上的最大距离。(这里的最大距离指的是这条路径上的所有数最大gcd>1)。
具体思路:首先,我们可以找出对于一个父亲节点,他和子节点能够在不是互素的前提下,对于他们每一个因子的个数。
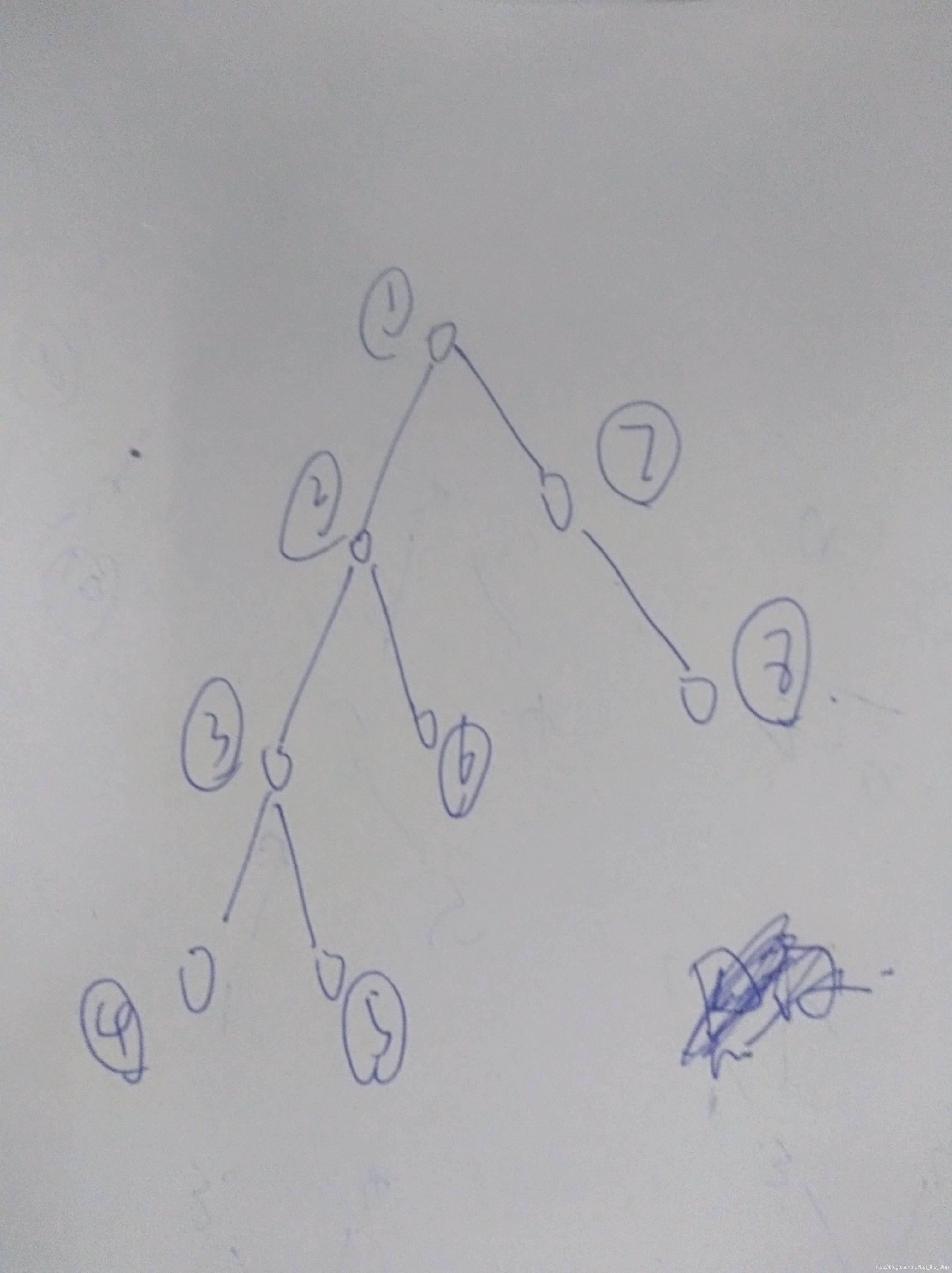
然后我们先dfs到底部,然后看他的每一个子节点之间产生的最大公因数是不是1,如果不是的话,我们就求这条路径上的最大值,在求最大值的时候,我们还是按照树的结构来,如图所示,从4号节点开始,4号节点更新之后会回到上一层,也就是3号节点,然后再求3号节点的所有因子和4号节点的因子是不是互素的,如果不是就从不是互素的这些状态里面找出一个最大值,然后在更新3号节点,这样更新下去就可以了。
注意:应该是先求最大状态再去更新父亲节点,如果先更新再去找最大值的话,会有一部分路径是重复的。举个例子,对于2,3,6这三个点,正确的解法是先求2和当前3号节点的最大距离,然后更新2号节点,然后再轮到6号节点,这个时候2号节点里面存储的是和3号节点之间的关系,我们再去求和6号节点之间的关系,这样就不会有路径重复了。
AC代码:
1 #include<bits/stdc++.h> 2 using namespace std; 3 # define ll long long 4 const int maxn = 4e5+100; 5 int a[maxn],num,head[maxn],maxx; 6 map<int,int>dis[maxn]; 7 struct node 8 { 9 int nex; 10 int to; 11 } edge[maxn]; 12 void init() 13 { 14 maxx=0; 15 num=0; 16 memset(head,-1,sizeof(head)); 17 } 18 int gcd(int n,int m) 19 { 20 if(n<m) 21 swap(n,m); 22 return n%m==0?m:gcd(m,n%m); 23 } 24 void addedge(int fr,int to) 25 { 26 edge[num].nex=head[fr]; 27 edge[num].to=to; 28 head[fr]=num++; 29 } 30 void dfs(int fr,int rt) 31 { 32 if(a[fr]>1) 33 { 34 dis[fr][a[fr]]=1; 35 } 36 for(int i=head[fr]; i!=-1; i=edge[i].nex) 37 { 38 int to=edge[i].to; 39 if(to==rt)continue; 40 dfs(to,fr); 41 for(auto t1:dis[fr]) 42 { 43 for(auto t2:dis[to]) 44 { 45 if(gcd(t1.first,t2.first)!=1) 46 { 47 maxx=max(maxx,t1.second+t2.second); 48 } 49 } 50 } 51 for(auto t1:dis[to]) 52 { 53 int tmp=gcd(a[fr],t1.first); 54 if(tmp==1) 55 continue; 56 dis[fr][tmp]=max(dis[fr][tmp],t1.second+1); 57 } 58 } 59 } 60 int main() 61 { 62 init(); 63 int n; 64 scanf("%d",&n); 65 int t1,t2; 66 for(int i=1; i<=n; i++) 67 { 68 scanf("%d",&a[i]); 69 if(a[i]!=1) 70 maxx=1; 71 } 72 for(int i=1; i<=n-1; i++) 73 { 74 scanf("%d %d",&t1,&t2); 75 addedge(t1,t2); 76 addedge(t2,t1); 77 } 78 dfs(1,1); 79 printf("%d\n",maxx); 80 return 0; 81 }


