矩阵树定理学习笔记。

由于过于难啃（懒）于是来记个笔记。

start

首先一个结论：

对于一个无向图 G ，它的生成树个数等于其基尔霍夫矩阵(Kirchhoff矩阵)任何一个N-1阶主子式的行列式的绝对值。

基尔霍夫矩阵可以由度数矩阵D-邻接矩阵A得到。

度数矩阵D：

\[D_{i,j}=[i==j]in_i \]

其中\(in_x\)表示x点度数。

邻接矩阵A:

\[A_{i,j}=[i!=j]w_{i,j} \]

其中\(w_{i,j}\)表示i，j两点之间边数。

不会证，记就完事了。

N-1阶主子式就是这个矩阵去掉某一行某一列之后的新矩阵。

然后就要求行列式了。

先是有个开始的柿子：

\[det(K)=\sum_p(-1)^{\tau (p)}\prod\limits_{i=1}^{n}K_{i,p_i} \]

其中\({\tau (p)}\)表示排列\(p\)中逆序对数，也说明要求从K中任意选的n个数行列互不相同。

暴力求解复杂度过高于是考虑优化。

行列式的性质

1. 交换一个矩阵的两行，行列式变号。
   这个很好证，首先K值肯定不变，然而交换了两行\(i,j\)之后，夹在i，j之间的变化量也一定是变一个偶数，但是ij之间的就变了一次，于是变号了。
2. 如果矩阵有两行(列)完全相同，则行列式为 0
   由1可得交换两行之后变号，但是交换之后整个矩阵不变所以只能是0
3. 如果矩阵的某一行(列)中的所有元素都乘以同一个数k，新行列式的值等于原行列式的值乘上数k。
   直接把柿子中提出来一个K即可。
   3.5 如果矩阵的某一行(列)中的所有元素都有一个公因子k，则可以把这个公因子k提到行列式求和式的外面。
4. 如果矩阵有两行(列)成比例(比例系数k)，则行列式的值为 0
   可以把大的一行提出来一个k，然后由2得到一定是0
5. 如果把矩阵的某一行(列)加上另一行(列)的k倍，则行列式的值不变。
   可以把新的求和柿子拆成两个柿子，一个是原来的柿子，一个是新加的k倍的柿子，由4得到后者一定是0，所以值不变。

求行列式

由上面几个性质，我们就可以求行列式了。
先偷个图：

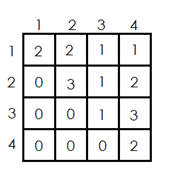
没错，是个上三角矩阵。那么它的行列式就是对角线的乘积，因为只有这时才能满足每一项都不是0.
那么我们如何把一个普通矩阵变成一个上三角矩阵呢？
看看性质5，没错，我们可以高斯消元！然后就可以愉快地求矩阵了！
对于计算过程中不允许出现实数的情况，可以采用辗转相除法。也可以使用逆元（如果有的话）

最后放个辗转相除的板子。

while(a[j][i]){
	int t=a[j][i]/a[i][i];
	F(k,i,n)a[i][k]-=1ll*a[j][k]*t%mod,a[i][k]+=a[i][k]<0?mod:0,a[i][k]-=a[i][k]>=mod?mod:0;
	std::swap(a[i],a[j]);ans=mod-ans;
}