noip模拟8
T1 星际旅行
题目描述


一个图存在欧拉路的条件是有\(2/0\)个点有奇数个出度,把一条无向边拆成两条,所以可以选择拆两个自环、一个自环一条边、连接同一个点的边。
先判断图是否是边联通,不联通则输出0
于是答案就是
\(\textrm{C}_{zi}^{2}\)+\(zi\)*\(bian\)+\(\sum_{i=1}^{n}\textrm{C}_{in_{i}}^{2}\)
其中\(zi\)就是自环总数,\(bian\)就是边总数,\(in_{i}\)表示\(i\)点出度。
Code
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
using namespace std;
namespace EMT{
#define F(i,a,b) for(register int i=a;i<=b;i++)
#define D(i,a,b) for(register int i=a;i>=b;i--)
#define pf printf
typedef long long ll;
#define int long long
inline ll read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x*f;}
inline void pi(int x){pf("%lld ",x);}inline void pn(){pf("\n");}
const int N=1e5+100;int co,head[N];
struct node{int next,to;}e[N<<1];inline void add(int next,int to){e[++co].next=head[next],e[co].to=to,head[next]=co;}
int zi,n,m,in[N],fn;bool v[N];
int h[N];
inline void dfs(int k){
v[k]=1;
queue<int>q;
q.push(k);
while(!q.empty()){
int x=q.front();q.pop();
for(register int i=head[x];i;i=e[i].next){
if(!v[e[i].to])v[e[i].to]=1,q.push(e[i].to);
}
}
}
inline short main(){
n=read();m=read();
F(i,1,m){
int a=read(),b=read();
if(a==b)zi++,h[a]++;
else add(a,b),add(b,a),in[a]++,in[b]++;
}
F(i,1,n)if(in[i]||h[i]){dfs(i);break;}
F(i,1,n)if(!v[i]&&(in[i]||h[i])){pi(0);return 0;}
fn+=zi*(zi-1)/2;
fn+=zi*co/2;
F(i,1,n)fn+=in[i]*(in[i]-1)/2;
pi(fn);return 0;
}
}
signed main(){return EMT::main();}
T2 砍树
题目描述

这个题不能二分,因为此题没有单调性。题意就是求一个最大的\(d\),满足
\(\sum_{i=1}^{n}\)(┌\(\frac{a_{i}}{d}\)┐\(*d-a_{i}\))\(<=k\)
将\(\sum_{i=1}^{n}a_{i}\)移项并将\(d\)除过去可得
\(\sum_{i=1}^{n}\)┌\(\frac{a_{i}}{d}\)┐\(<=\frac{k+\sum_{i=1}^{n}a_{i}}{d}\)
其中左边一项向下取整依然等价,所以就变成了
\(\sum_{i=1}^{n}\)┌ \(\frac{a_{i}}{d}\) ┐ \(<=\)└\(\frac{k+\sum_{i=1}^{n}a_{i}}{d}\) ┘
┌ ┐代表向上取整,└ ┘代表向下取整
于是我们可以找出每一个└\(\frac{k+\sum_{i=1}^{n}a_{i}}{d}\) ┘值的最大临界值\(d\),因为\(d\)最大时\(\sum_{i=1}^{n}\)┌ \(\frac{a_{i}}{d}\) ┐ 才最小,也最符合题意。
预处理后暴力判断即可。
Code
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
namespace EMT{
#define F(i,a,b) for(register int i=a;i<=b;i++)
#define D(i,a,b) for(register int i=a;i>=b;i--)
#define f(x) for(register int i=head[x],j;i;i=e[i].next)
#define pf printf
typedef long long ll;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x*f;}
inline void pi(ll x){pf("%lld ",x);}inline void pn(){pf("\n");}
const int N=110;int k,n,cnt,a[N];ll rec[1000040],T;
inline bool check(ll x){ll co=0;F(i,1,n){co+=ceil((double)a[i]/x);if(co>T/x)return 0;}return 1;}
inline short main(){
n=read();k=read();T=k;
F(i,1,n)a[i]=read(),T+=a[i];
F(i,1,sqrt(T)){
rec[++cnt]=T/(T/i);
rec[++cnt]=T/i;
}
sort(rec+1,rec+cnt+1);int len=unique(rec+1,rec+cnt+1)-rec-1;
D(i,len,1){if(check(rec[i])){pi(rec[i]);return 0;}}
return 0;
}
}
signed main(){return EMT::main();}
T3 超级树
题意描述
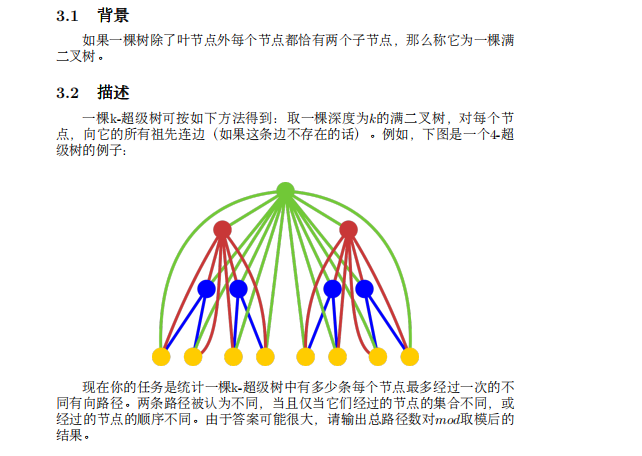
考虑\(dp[i][j]\)表示一棵\(i\)超级树,有\(j\)条点不重复的路径的方案数。考虑\(dp[i]\)对\(dp[i+1]\)的
贡献:枚举左子树和右子树的路径条数l、r,记\(num=dp[i][l]*dp[i][r]\),则有
• 什么也不做 \(dp[i+1][l+r]+=num\)
• 根自己作为一条新路径 \(dp[i+1][l+r+1]+=num\)
• 根连接到左子树(或右子树)的某条路径上 \(dp[i+1][l+r]+=2*num*(l+r)\)
• 根连接左子树和右子树的各一条路径 \(dp[i+1][l+r-1]+=2*num*l*r\)
• 根连接左子树(或右子树)的两条路径 \(dp[i+1][l+r-1]+=num*(l*(l-1)+r*(r- 1))\)
边界为\(dp[1][0]=dp[1][1]=1\),答案为\(dp[k][1]\)。
Code
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
namespace EMT{
#define F(i,a,b) for(register int i=a;i<=b;i++)
#define D(i,a,b) for(register int i=a;i>=b;i--)
#define pf printf
typedef long long ll;
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x*f;}
inline void pi(int x){pf("%d ",x);}inline void pn(){pf("\n");}
const int N=310;
ll tot,mod;int k;
ll ans,dp[N][N];
inline short main(){
k=read();mod=read();
dp[1][1]=dp[1][0]=1;
F(i,1,k-1){
F(l,0,k){
F(r,0,k-l){
if(dp[i][l]&&dp[i][r]){
ll num=dp[i][l]*dp[i][r]%mod;
(dp[i+1][l+r]+=num)%=mod;
(dp[i+1][l+r+1]+=num)%=mod;
(dp[i+1][l+r]+=2*num*(l+r))%=mod;
(dp[i+1][l+r-1]+=2*num*l*r)%=mod;
(dp[i+1][l+r-1]+=num*(l*(l-1)+r*(r-1)))%=mod;
}
}
}
}
pi(dp[k][1]%mod);
return 0;
}
}
int main(){return EMT::main();}
T4 求和
题目描述

一开始\(dfs\)预处理即可。
Code
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
namespace EMT{
#define F(i,a,b) for(register int i=a;i<=b;i++)
#define D(i,a,b) for(register int i=a;i>=b;i--)
#define f(x) for(register int i=head[x],j;i;i=e[i].next)
#define pf printf
typedef unsigned long long ll;
#define int long long
inline int read(){int x=0,f=1;char ch=getchar();while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x*f;}
inline void pi(ll x){pf("%lld ",x);}inline void pn(){pf("\n");}
const ll mod=998244353;const int N=3e5+100;int n,m,head[N],co,deep[N],fa[N][21];ll sum[N][51];
struct node{int next,to;}e[N<<1];inline void add(int next,int to){e[++co].next=head[next],e[co].to=to,head[next]=co;}
inline ll ksm(ll a,int b){
ll ans=1;
while(b){
if(b&1)ans=ans*a%mod;
a=a*a%mod;
b>>=1;
}return ans;
}
inline void dfs(int k,int Fa){
F(i,1,50)sum[k][i]=(sum[Fa][i]+ksm(deep[k],i))%mod;
f(k){
j=e[i].to;if(j==Fa)continue;deep[j]=deep[k]+1;
fa[j][0]=k;F(l,1,20)if((1<<l)<=deep[j])fa[j][l]=fa[fa[j][l-1]][l-1];else break;
dfs(j,k);
}
}
inline int getlca(int a,int b){
if(deep[a]<deep[b])swap(a,b);
D(i,20,0)if((1<<i)<=deep[a]-deep[b])a=fa[a][i];
if(a==b)return a;
D(i,20,0)if(fa[a][i]!=fa[b][i])a=fa[a][i],b=fa[b][i];
return fa[a][0];
}
inline short main(){
n=read();
F(i,1,n-1){int x=read(),y=read();add(x,y);add(y,x);}
m=read();dfs(1,0);
F(i,1,m){
int a=read(),b=read(),k=read();
int lca=getlca(a,b);
if(lca==a){
pi(((sum[b][k]-sum[fa[a][0]][k])%mod+mod)%mod);pn();
}else if(lca==b){
pi(((sum[a][k]-sum[fa[b][0]][k])%mod+mod)%mod);pn();
}else{
pi(((sum[a][k]+sum[b][k]-sum[lca][k]-sum[fa[lca][0]][k])%mod+mod)%mod);pn();
}
}
return 0;
}
}
signed main(){return EMT::main();}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号