noip模拟4
前言
淦,以后再也不打表了,打表一小时还不如去码标程。
T1 随
题目描述:
给出 \(n\) 个正整数 $ a1,a2…an$ 和一个质数 \(mod\) .一个变量 \(x\) 初始为 \(1\) .进行 $ m$ 次操作.每次在 \(n\) 个数中随机选一个 \(ai\),
然后问 \(m\) 次操作之后 \(x\) 的取值的期望. 答案一定可以表示成 \(a/b\) 的精确分数形式.a和b可能很大,所以只需要输出\(a*b^{10^9+5}\)模\(10^9+7\)的结果.
学到了新知识——原根。
考场上感觉到要靠多项式的乘法做题了, 奈何蒟弱太弱,根本想不出正解。
要是不是乘法,是加法多好?
唉?这个原根不就是我偷懒用加法的好助手吗?
解释一下:
对于 任意一个数 \(num\subset[1,mod-1]\) ,原根都有一个唯一的指数\(p^i\)来表示它。
而\(p^a*p^b=p^{a+b}\)就可以使我的偷懒加法大计实现。
那么求原根就成为了本题的要点。因此,蒟弱特意去学了一下快亿点的原根求法。
具体教程见这里
但文中有一处码好像错了?评论里也有大佬指出了,就是最后判断原根时除素数最后剩下的要加进去。
if(k>1)pm[++cntpm]=k;
具体流程就是(引用一下:
求任何一个质数x的任何一个原根,一般就是枚举2到x-1,并检验。有一个方便的方法就是,求出x-1所有不同的质因子p1,p2...pm,对于任何2<=a<=x-1,判定a是否为x的原根,只需要检验a((x-1)/p1),a((x-1)/p2),...a^((x-1)/pm)这m个数中,是否存在一个数mod x为1,若存在,a不是x的原根,否则就是x的原根。
于是先筛好素数:
void getprime(){for(int i=2;i<num;i++){
if(!f[i]){
f[i]=1;
prime[++primecnt]=i;
}
for(int j=1;j<primecnt&&i*prime[j]<num;j++){
f[i*prime[j]]=1;
if(i%prime[j])break;
}
}
}
再判断:
bool judge(int x){
int pm[1010],cntpm=0;
int k=p-1;
F(1,primecnt){
bool can=0;
while(!(k%prime[i]))k/=prime[i],can=1;
if(can)pm[++cntpm]=prime[i];
if(k==1)break;
}
if(k>1)pm[++cntpm]=k;
bool can=1;
F(1,cntpm)if(ksm(x,(p-1)/prime[i],p)==1){can=0;break;}
return can;
}
最后矩阵快速幂即可。
Code
#include<bits/stdc++.h>
using namespace std;
namespace EMT{
#define pf printf
#define db double
#define F(a,b) for(register int i=a;i<=b;i++)
#define f(x) for(register int i=head[x],j;i;i=e[i].next)
#define int long long
const int N=1e5+100,Mod=1e9+7,num=1100;
inline int read(){int x=0;char ch=getchar();while(ch<'0'||ch>'9')ch=getchar();while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x;}
inline void pn(){pf("\n");}inline void pt(){pf(" ");}inline void pi(int x){pf("%lld ",x);}inline void ps(int a[],int size){F(1,size)pi(a[i]);pn();}
int n,m,primecnt,p,al[N],ci[1010],qp[1010],prime[num],yg,a[N],ans[N],res[N],base[N];bool f[num];
int ksm(int a,int b,int p){int ans=1;while(b){if(b&1)ans=ans*a%p;a=a*a%p;b>>=1;}return ans;}
void basemul(){
F(0,p-1)for(int j=0;j<=p-1;j++)(res[j]+=base[i]*base[(j-i+p)%p])%=Mod;
F(0,p-1)base[i]=res[i],res[i]=0;
}
void ansmul(){
F(0,p-1)for(int j=0;j<=p-1;j++)(res[j]+=ans[i]*base[(j-i+p)%p])%=Mod;
F(0,p-1)ans[i]=res[i],res[i]=0;
}
void getprime(){for(int i=2;i<num;i++){
if(!f[i]){
f[i]=1;
prime[++primecnt]=i;
}
for(int j=1;j<primecnt&&i*prime[j]<num;j++){
f[i*prime[j]]=1;
if(i%prime[j])break;
}
}
}
bool judge(int x){
int pm[1010],cntpm=0;
int k=p-1;
F(1,primecnt){
bool can=0;
while(!(k%prime[i]))k/=prime[i],can=1;
if(can)pm[++cntpm]=prime[i];
if(k==1)break;
}
if(k>1)pm[++cntpm]=k;
bool can=1;
F(1,cntpm)if(ksm(x,(p-1)/prime[i],p)==1){can=0;break;}
return can;
}
int ask(){F(2,num)if(judge(i))return i;}
signed main()
{
ans[0]=1;
getprime();n=read();m=read();p=read();yg=ask();
int now=1;const int P=ksm(n,Mod-2,Mod);
for(int i=0;i<p-1;i++)ci[now]=i,qp[i]=now,now=now*yg%p;p--;
F(1,n)a[i]=ci[read()];
F(1,n)(base[a[i]]+=P)%=Mod;
while(m){
if(m&1)ansmul();
basemul();
m>>=1;
}int Ans=0;
F(0,p-1)(Ans+=ans[i]*qp[i])%=Mod;
pi(Ans);pn();return 0;
}
}
int main(){return EMT::main();}
T2 单
题目描述:
对于一棵树,认为每条边长度为\(1\),每个点有一个权值\(a[i]\).\(dis(u,v)\)为点u到v的最短路径的边数.\(dis(u,u)=0\).对每个点求出一个重要程度.点x的重要程度\(b[x]\)定义为其他点到这个点的距离乘上对应的点权再求和.即:
\(b[x]=a[1]*dis(1,x)+a[2]*dis(2,x)+....+a[n]*dis(n,x)\)
现在有很多树和对应的\(a\)数组,并求出了\(b\)数组.不幸的是,记录变得模糊不清了.幸运的是,树的形态完好地保存了下来,\(a\)数组和\(b\)数组至少有一个是完好无损的,但另一个数组完全看不清了.
希望你求出受损的数组.多组数据.
考试高斯消元骗40分失败,哭唧唧~
好了,话休繁絮,开始~
- 对于已知\(a\)数组的情况,用数组\(size[i]\)来表示节点\(i\)的子结点(包括自己)的权值之和,用\(deep\)表示深度,那么先dfs一次就可以求出\(b[1]\),即:
\(b[1]=\sum_{i=2}^{n}a[i]*deep[i]\)
我们假设对于节点\(k\),有\(ls\)与\(rs\)(左右节点),那么再次进行DFS,
结点\(ls\)的\(b[ls]\)就比\(k\)
离左子树结点距离少了1,则权值少了\(size[ls]*1\),
离其他结点距离多了1,则权值多了\((size[1]-size[ls])*1\)
推广到多个子结点也是一样的。所以有:
\(b[son]=b[fa]-size[ls]+size[1]-size[ls]=b[fa]+size[1]-2*size[ls]\)
2.对于已知\(b\) 数组的情况,有亿点不方便写(其实是懒,附张图吧:
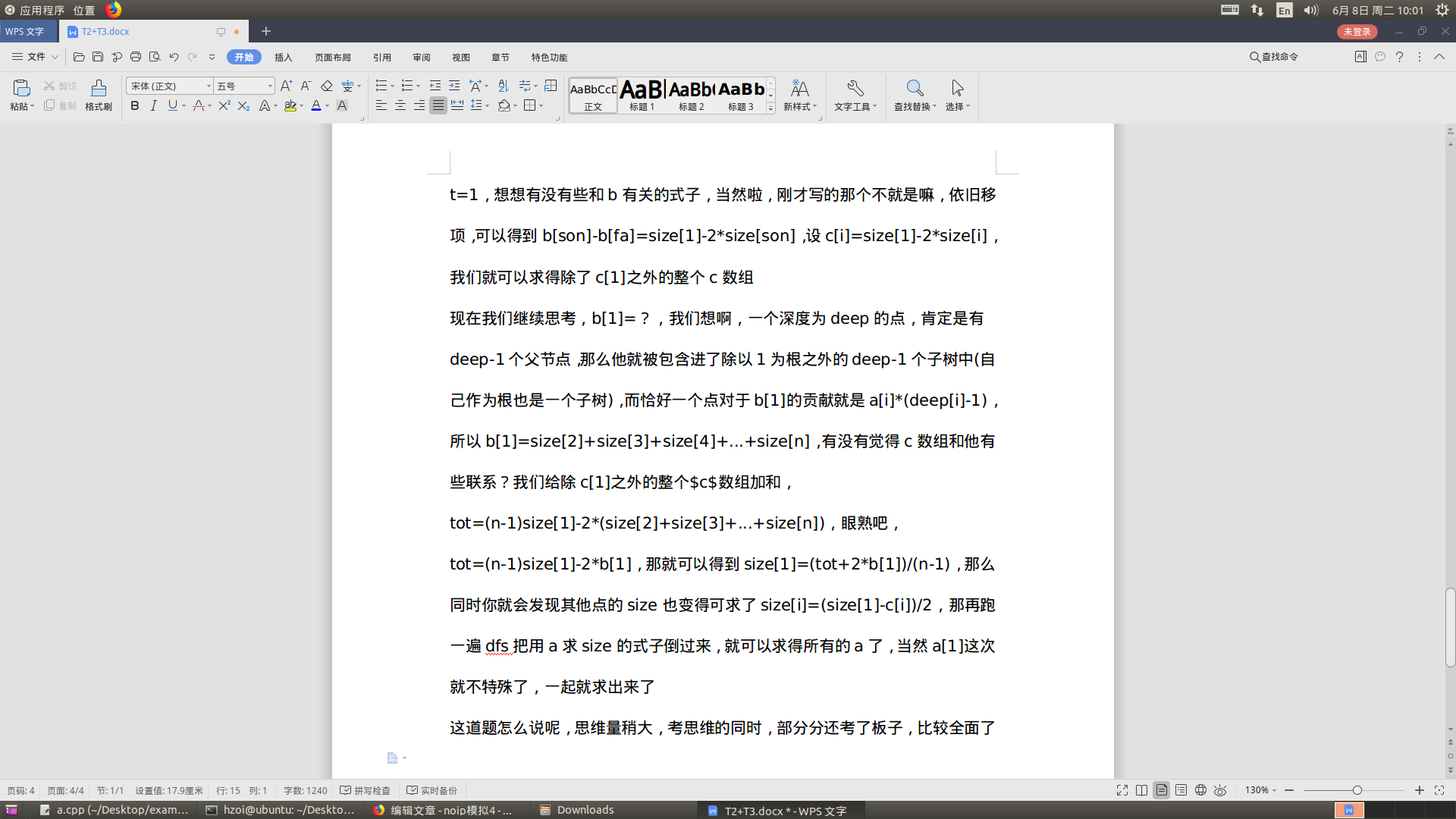
Code
#include<bits/stdc++.h>
using namespace std;
namespace EMT{
#define pf printf
#define db double
#define F(a,b) for(register int i=a;i<=b;i++)
#define f(x) for(register int i=head[x],j;i;i=e[i].next)
#define int long long
inline int read(){int x=0;char ch=getchar();while(ch<'0'||ch>'9')ch=getchar();while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x;}
inline void pn(){pf("\n");}inline void pt(){pf(" ");}inline void pi(int x){pf("%lld ",x);}inline void ps(int a[],int size){F(1,size)pi(a[i]);pn();}
const int N=2e5+100;
int n,m,a[N],b[N],deep[N],size[N],head[N],c[N],co,T,sum;struct node{int next,to;}e[N<<1];
inline void add(int next,int to){e[++co].next=head[next],e[co].to=to,head[next]=co;}
inline void dfs(int k,int fa){
f(k){
j=e[i].to;if(j==fa)continue;
deep[j]=deep[k]+1;dfs(j,k);
size[k]+=size[j];
}b[1]+=a[k]*deep[k];
}
inline void Dfs(int k,int fa){
f(k){
j=e[i].to;if(j==fa)continue;
b[j]=b[k]+size[1]-2*size[j];
Dfs(j,k);
}
}
inline void tfs(int k,int fa){
f(k){
j=e[i].to;if(j==fa)continue;
c[j]=b[j]-b[k];
tfs(j,k);
}sum+=c[k];
}
inline void Tfs(int k,int fa){
f(k){
j=e[i].to;if(j==fa)continue;
Tfs(j,k);a[k]-=size[j];
}
}
signed main(){
//freopen("single8.in","r",stdin);
//freopen("B.out","w",stdout);
T=read();
while(T--){
n=read();co=0;memset(head,0,sizeof(head));memset(deep,0,sizeof(deep));sum=0;
memset(a,0,sizeof(a));memset(b,0,sizeof(b));memset(c,0,sizeof(c));memset(size,0,sizeof(size));
F(1,n-1){int x=read(),y=read();add(x,y);add(y,x);}
m=read();
if(!m){
F(1,n)a[i]=read(),size[i]=a[i];
dfs(1,0);
Dfs(1,0);ps(b,n);
}
else{
F(1,n)b[i]=read();
tfs(1,0);a[1]=size[1]=(sum+2*b[1])/(n-1);
F(2,n)a[i]=size[i]=(size[1]-c[i])/2;
Tfs(1,0);ps(a,n);
}
}
return 0;
}
}
signed main(){return EMT::main();}
T3 题
题目描述:
你在平面直角坐标系上.
你一开始位于(0,0).
每次可以在上/下/左/右四个方向中选一个走一步.
即:从(x,y)走到(x,y+1),(x,y-1),(x-1,y),(x+1,y)四个位置中的其中一个.
允许你走的步数已经确定为n.现在你想走n步之后回到(0,0).但这太简单了.你希望知道有多少种不同的方案能够使你在n步之后回到(0,0).当且仅当两种方案至少有一步走的方向不同,这两种方案被认为是不同的.
答案可能很大所以只需要输出答案对109+7取模后的结果.(109+7=1000000007,1和7之间有8个0)
这还是太简单了,所以你给能够到达的格点加上了一些限制.一共有三种限制,加上没有限制的情况,一共有四种情况,用0,1,2,3标号:
0.没有任何限制,可以到达坐标系上所有的点,即能到达的点集为{(x,y)|x,y为整数}
1.只允许到达x轴非负半轴上的点.即能到达的点集为{(x,y)|x为非负数,y=0}
2.只允许到达坐标轴上的点.即能到达的点集为{(x,y)|x=0或y=0}
3.只允许到达x轴非负半轴上的点,y轴非负半轴上的点以及第1象限的点.即能到达的点集为{(x,y)|x>=0,y>=0}题
就是这个题让我花费1h打表最后成功多得10分,好(wo)耶(qu)
本题用到了卡特兰数,是蒟弱没学过的知识,但还好有题解文档,给张图吧~
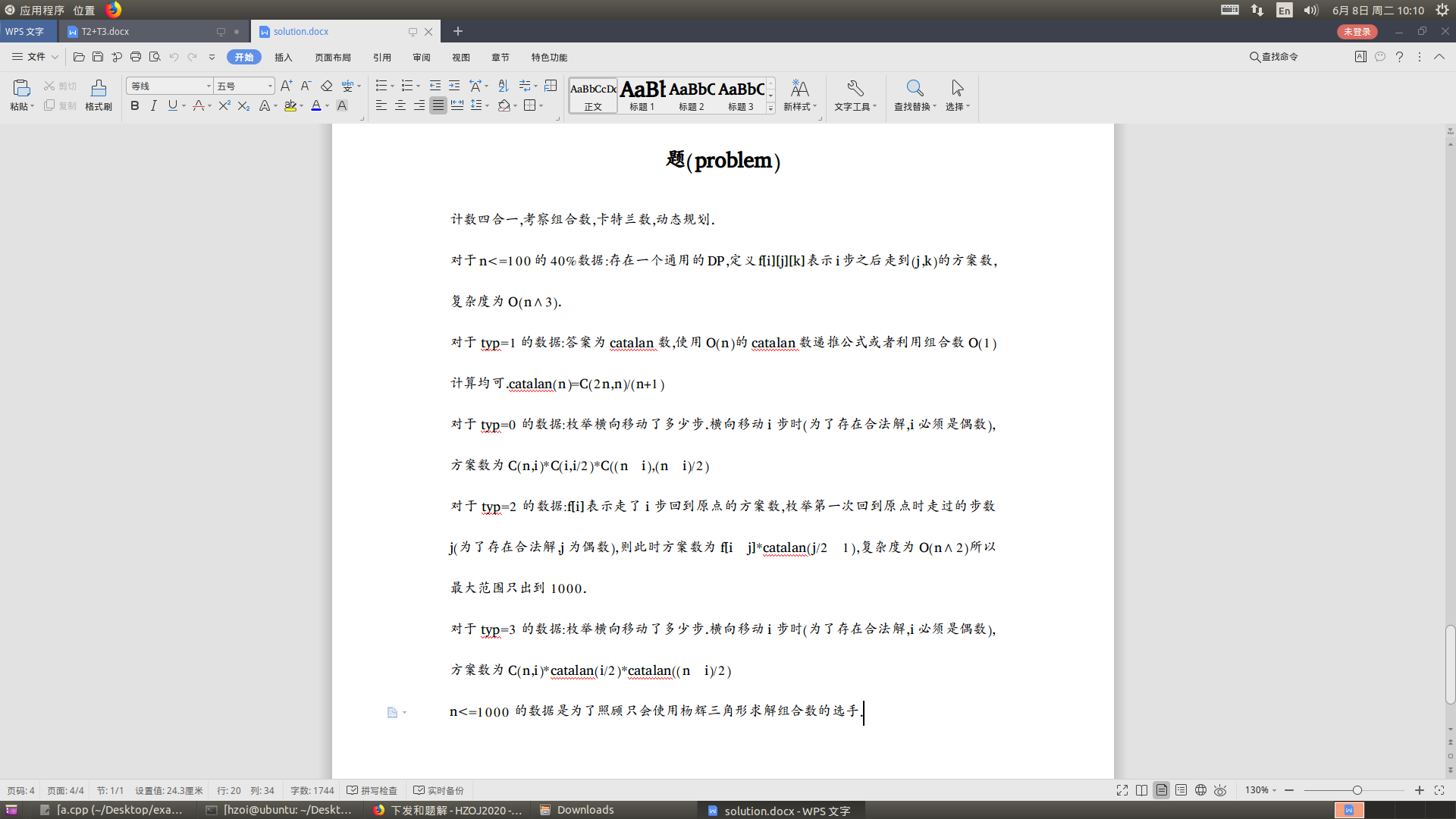
用到了卡特兰数公式:
\(Cat(n)=\frac{_{2n}^{n}\textrm{C}}{n+1}\)
C的话,组合数求个阶乘逆元就出来啦~:
Code
#include<bits/stdc++.h>
using namespace std;
namespace EMT{
#define pf printf
#define db double
#define F(a,b) for(register int i=a;i<=b;i++)
#define f(x) for(register int i=head[x],j;i;i=e[i].next)
#define int long long
const int N=1e5+100;
inline int read(){int x=0;char ch=getchar();while(ch<'0'||ch>'9')ch=getchar();while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x;}
inline void pn(){pf("\n");}inline void pt(){pf(" ");}inline void pi(int x){pf("%lld ",x);}inline void ps(int a[],int size){F(1,size)pi(a[i]);pn();}
int n,typ,ans,jc[N],f[N],inv[N];const int mod=1e9+7;int ksm(int a,int b){int ans=1;while(b){if(b&1)ans=ans*a%mod;a=a*a%mod;b>>=1;}return ans;}
int C(int n,int m){if(m==0||m==n)return 1;if(n<m)return 0;return jc[n]*inv[m]%mod*inv[n-m]%mod;}
int Ca(int n){return C(2*n,n)%mod*ksm(n+1,mod-2)%mod;}
int main()
{
n=read();typ=read();
jc[0]=jc[1]=1;inv[0]=inv[1]=1;
F(2,n)inv[i]=(mod-mod/i)%mod*inv[mod%i]%mod;
F(2,n)inv[i]=inv[i]*inv[i-1]%mod;
F(2,n)jc[i]=jc[i-1]*i%mod;
if(typ==0){
for(int i=0;i<=n;i+=2){
ans=(ans+C(n,i)*C(i,i/2)%mod*C(n-i,(n-i)/2))%mod;
}
pi(ans);return 0;
}
if(typ==1){
ans=Ca(n/2);
pi(ans);return 0;
}
if(typ==2){n/=2;f[0]=1;f[1]=4;
for(int i=2;i<=n;i++)
for(int j=1;j<=i;j++)
f[i]=(f[i]+f[i-j]%mod*4*Ca(j-1)%mod)%mod;
pi(f[n]);
return 0;
}
if(typ==3){
for(int i=0;i<=n;i+=2){
ans=(ans+C(n,i)%mod*Ca(i/2)%mod*Ca((n-i)/2)%mod)%mod;
}
pi(ans);return 0;
}
}
}
signed main(){return EMT::main();}
T4 大佬
题目描述:


设\(f[i][j]\)表示目前是第\(i\)天,血量是\(j\)的最多攻击天数。
那么可以进行动态规划,式子是:
\(f[i][j-a[i]]=max(f[i-1][j]+1)\)
\(f[i][j-a[i]+w[i]]=max(f[i-1][j]);\)
dp完后,
从零枚举能攻击的最多天数。
用class类(\(\approx\)结构体)的\(d\)表示天数,\(f\)表示战斗力,\(l\)表示等级,
用pair和map来存储能到达的所有情况。
处理完后,利用pair先排序第一关键字的性质sort pair 好耶,
讨论是否能够达到击败各个大佬的水平即可。
Code
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
#include<cstdio>
#include<vector>
#include<queue>
#include<map>
using namespace std;
namespace EMT{
#define int long long
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
int read(){int x=0;char ch=getchar();while(ch<'0'||ch>'9')ch=getchar();while(ch>='0'&&ch<='9')x=x*10+ch-'0',ch=getchar();return x;}
#define pf printf
#define fr first
#define mp make_pair
#define se second
#define F(i,a,b) for(register int i=a;i<=b;i++)
const int N=110;
pair<int,int>p[N*10000];
int tot;
inline void pi(int x){pf("%lld ",x);}inline void pt(){pf(" ");}inline void pn(){pf("\n");}inline void ps(int x[],int size){F(i,1,size)pi(x[i]);pn();}
int n,m,mc,a[N],w[N],c[N],f[N][N],maxn=-0x7fffffff,day=maxn;
class emt{public:int d,f,l;emt(int x,int y,int z):d(x),f(y),l(z){}};queue<emt>q;
map<pair<int,int>,bool>hash;
inline void bfs(){
q.push(emt(1,1,0));
while(!q.empty()){
emt u=q.front();q.pop();
if(u.d==day)continue;
q.push(emt(u.d+1,u.f,u.l+1));
if(u.l>1&&u.l*u.f<=maxn&&!hash[mp(u.l*u.f,u.d+1)]){
q.push(emt(u.d+1,u.f*u.l,u.l));
p[++tot]=mp(u.l*u.f,u.d+1);
hash[mp(u.l*u.f,u.d+1)]=1;
}
}
}
int main(){
n=read();m=read();mc=read();
F(i,1,n)a[i]=read();F(i,1,n)w[i]=read();F(i,1,m)c[i]=read(),maxn=max(maxn,c[i]);
F(i,1,n)F(j,a[i],mc)f[i][j-a[i]]=max(f[i][j-a[i]],f[i-1][j]+1),f[i][min(j-a[i]+w[i],mc)]=max(f[i][min(j-a[i]+w[i],mc)],f[i-1][j]);
F(i,1,n)F(j,1,mc)day=max(day,f[i][j]);
bfs();
sort(p+1,p+tot+1);
F(i,1,m){
if(c[i]<=day){pi(1);pn();continue;}
int minn=0x7fffffff;bool can=0;
for(register int j=tot,k=1;j>=1;j--){
while(k<tot&&p[j].fr+p[k].fr<=c[i])
minn=min(minn,p[k].se-p[k].fr),k++;
if(minn+c[i]-p[j].fr<=day-p[j].se){can=1;break;}
if(p[j].fr<=c[i]&&c[i]-p[j].fr<=day-p[j].se){can=1;break;}
}
pi(can);pn();
}
}
}
signed main(){return EMT::main();}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号