Motion Planning for Mobile Robots 学习笔记7

目录

• Outline 大纲
• Uncertainties in Planning 规划中的不确定性
  • 按不确定性的由来分类
  • 按机器人可利用信息量分类（数学角度）
• Planning with Uncertainties 存在不确定性下的规划
  • 双决策者模型
  • 单步问题定义
    • A Game Against Nature（Independent Game）独立博弈
    • Nature Knows the Robot Action（Dependent Game）从属博弈
  • 单步问题两种解法
    • One-step Worst-Case Analysis 一步最坏情况分析
    • One-step Expected-Case Analysis 一步期望情况分析
  • 多步情况问题定义
    • Discrete Planning with Nature 存在不确定性下的离散规划
    • Multi-step Discrete Planning with Nature 存在不确定性下的多步离散规划
• Markov Decision Process 马尔可夫决策过程
  • MDP与Planning
  • MDP建模的例子
  • 求解上述例子
• Minimax Cost Planning
  • 解法
  • 示例
  • Nondeterministic Dijkstra
    • 思考
    • Pros and Cons
• Expected Cost Planning
  • 递归公式
  • 例子
  • Value Iteration(VI) 值迭代算法
    • 算法概述
    • 算法特性
    • 算法示例
    • 思考
    • Pros and Cons
• Real Time Dynamic Programming
• Homework

MDP-Based Planning

以往：根据起点与终点选取路径。
决策树的概念，根据环境的动态变化选取最优的路径。

Outline 大纲

提出问题：

1. Uncertainties in Planning
2. Planning with Uncertainties
3. Markov Decision Process

解决问题：
4. Minimax Cost Planning
5. Expected Cost Planning
6. Real Time Dynamic Programming

Uncertainties in Planning 规划中的不确定性

到现在为止，假设机器人在执行动作完美无缺，对状态有充分了解的情况下没有任何不确定性。

按不确定性的由来分类

不确定性来自于：感知和执行的不确定性。因为，在实际应用中，执行和状态估计都不是完美的。

• 执行不确定性：打滑，崎岖的地形，风（的影响），空气阻力，控制误差等
• 状态估计不确定性：传感器噪声，校准误差，估计不完善，局部可观察性等。
  

左图是机器人打滑；右图是两机器人捉迷藏，彼此难以判断对方下一时刻的位置

按机器人可利用信息量分类（数学角度）

从数学角度来看，不确定性可以分为两类，它们表示机器人可以使用多少信息（知道多少信息）。
不确定性模型

• 不确定性：机器人不知道会受到哪种类型的不确定性或干扰。
• 概率：机器人通过观察和收集统计数据来估计不确定性。

Planning with Uncertainties 存在不确定性下的规划

双决策者模型

之前的运动规划中，只有机器人一个参与者。但在存在不确定性的情况下，需要引入另一个参与者。
为了正式描述这个概念，我们首先介绍两个决策者来对不确定性的产生建模，然后对具有不确定性的计划类型进行建模。
决策者

• 机器人（Robot）是基于完全已知的状态和完美执行来执行计划的主要决策者。
• 自然（Nature）给机器人制定的计划的执行增加了不确定性（产生所有的干扰），这对于机器人来说是无法预测的。

单步问题定义

核心问题：考虑到与自然界的博弈，机器人的最佳决策是什么？

A Game Against Nature（Independent Game）独立博弈

• 一个非空集\(U\)称为机器人动作空间。每个\(u\in U\)都称为机器人动作。
• 一个非空集\(\Theta\)称为自然动作空间。每个\(\theta \in \Theta\)被称为自然动作。
  两个动作空间相互独立。
• 函数\(L:U\times \Theta \rightarrow \mathbb{R}\cup \{\infty\}\)，称为成本函数或负回报函数。

通过优化\(L\)可以在自然参与下，寻找机器人的最优规划。

Nature Knows the Robot Action（Dependent Game）从属博弈

• 一个非空集\(U\)称为机器人动作空间。每个\(u\in U\)都称为机器人动作。
• 对于每个每个\(u\in U\)，一个非空集\(\Theta\)称为自然动作空间。
  自然动作空间依赖于机器人动作空间。
• 函数\(L:U\times \Theta \rightarrow \mathbb{R}\cup \{\infty\}\)，称为成本函数或负回报函数。

单步问题两种解法

One-step Worst-Case Analysis 一步最坏情况分析

• 在非确定性模型下，独立博弈中的\(P(\theta)\)和从属博弈中的\(P(\theta |u_k)\)是未知的；
• 机器人无法预测自然的行为，可以假设自然会故意选择会导致成本最高（对机器人最不利）的动作。
• 因此，通过假设最坏的情况来做出决策是合理的。
  

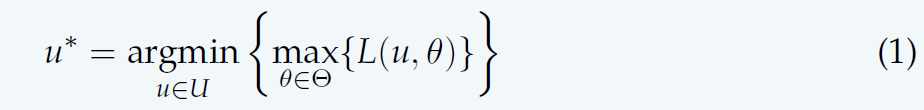
One-step Expected-Case Analysis 一步期望情况分析

• 在概率模型下，独立博弈中的\(P(\theta)\)和从属博弈中的\(P(\theta |u_k)\)是已知（不精准，已知其规律或分布）的；
• 假定已观察到所应用的自然动作，并且自然在动作选择中采用了随机策略。
• 因此，我们优化其平均代价的期望。
  

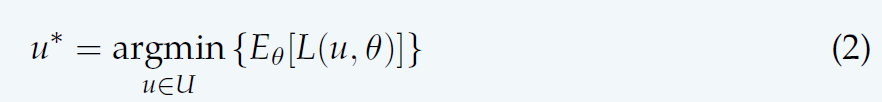
多步情况问题定义

Discrete Planning with Nature 存在不确定性下的离散规划

• 【1】具有初始状态\(x_s\)和目标集\(X_F\subset X\)的非空状态空间\(X\)。
  
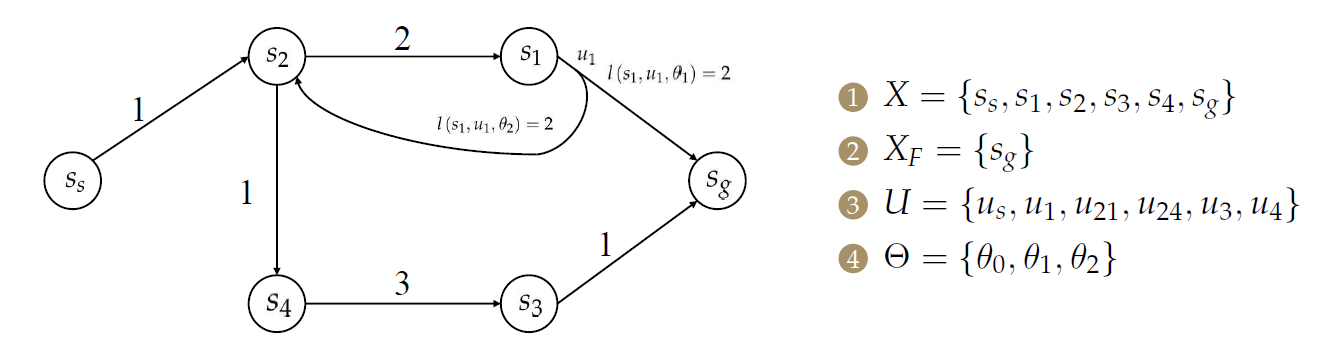
• 【2】对于每个状态\(x\in X\)，有一个有限且非空的机器人动作空间\(U(x)\)。对于每个\(x\in X\)和\(u\in U(x)\)，有一个有限且非空的自然动作空间\(\Theta (x,u)\)。
  对于上图而言，机器人在\(s_s\)处执行\(u_s\)到达\(s_2\)，而在\(s_1\)处机器人执行\(u_1\)会受到不同的自然干扰\(\theta_1\)或\(\theta_2\)，使之到达不同的状态（\(s_2\)或\(s_g\)）。
  在此处，\(\theta_0\)为不施加干扰。

Multi-step Discrete Planning with Nature 存在不确定性下的多步离散规划

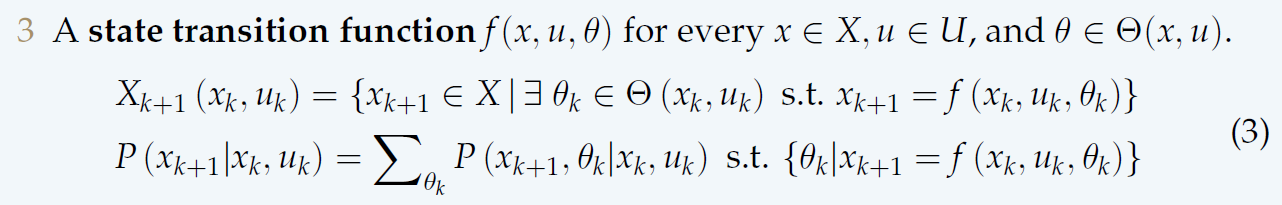
（接上述步骤）

• 【3】多步情况下需要对每个\(x\in X\)、\(u\in U(x)\)和\(\theta \in \Theta(x,u)\)定义状态转移方程\(f(x,u,\theta)\)
  状态转移方程的结果不是唯一的，在离散情况下为集合（并有相应的概率），在连续情况下呈现一定的分布。
  【第一行】对于离散情况，对于每个状态机器对于的动作，枚举自然的各种扰乱，随之产生下一时刻的状态。
  【第二行】对于连续情况，\(x_{k+1}\)与\(\theta_k\)服从一个依赖于\(x_k\)和\(u_k\)的联合概率分布，对其按\(\theta_k\)积分，可得到连续情况下的下一时刻分布。
  
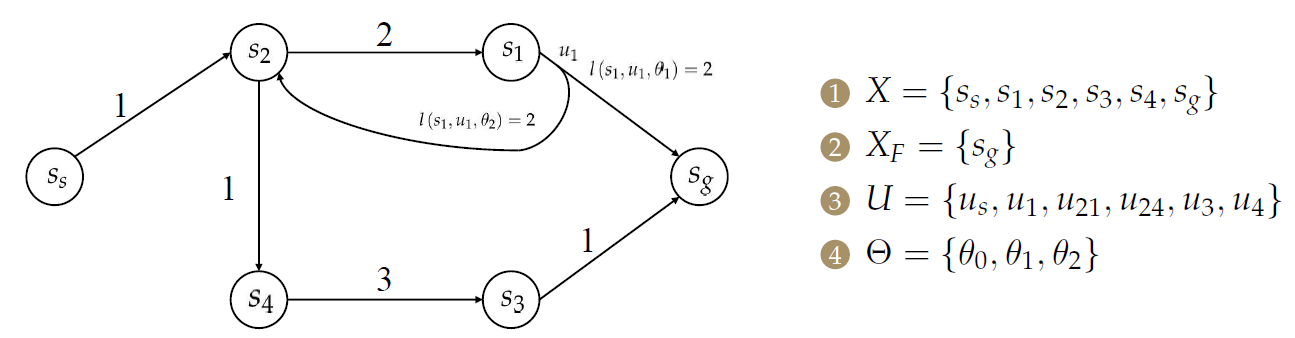
  使用离散状态下的计算方法：
  在机器人在\(s_s\)处执行\(u_s\)，由于自然的动作只有\(\theta_0\)，机器人的动作也只有\(u_s\)，因此其只能到达\(s_2\)。
  而在\(s_1\)处机器人执行\(u_1\)会受到不同的自然干扰\(\theta_1\)或\(\theta_2\)，因此，其\(X_{k+1}\)有两个元素，使之到达不同的状态（\(s_2\)或\(s_g\)）。
• 【4】不同于单步的规划，相应定义以\(k\)表示的一组阶段（stages）。也即机器人的规划由若干个连续的步骤组成。
  以\(k＝1\)开始并且无限期地继续或者以最大阶段\(k＝K+1＝F\)结束。
  

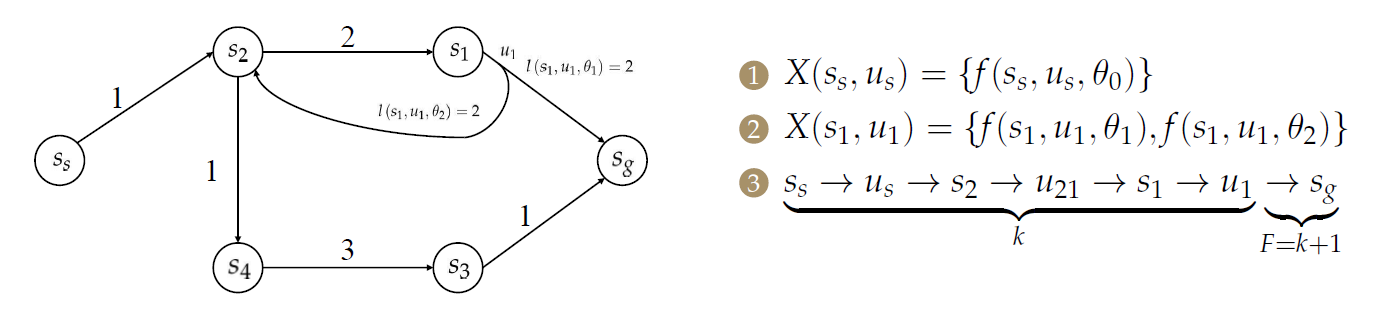
• 【5】与单步规划类似，相应定义代价函数\(L\)。最简单的方法是枚举计算。
  \(l\)代表单步的代价函数，从\(k=1\)累加到\(k=K\)也即到达终点，最后加上终点处的代价\(l_F\)。
  从中选择代价最小的\(L\)，其对应的\(u_k\)也即最优决策。
  但事实上，\(u_k\)往往是以决策树的形式存在的。

Markov Decision Process 马尔可夫决策过程

MDP与Planning

上一章中使用规划的建模方法对存在不确定性下的规划进行描述，但在Learning领域有现成的框架MDP可以解决这一问题。

事实上，只是使用了不同的符号，其实质是一样的。
具有不确定性的计划的第一个困难（也可能是最为困难的）在于使用MDP模型正确地表达我们的问题，而非求解一个MDP问题。
例如：该问题的状态空间是什么？动作空间是什么？转移函数（transition function）是什么？如何定义代价函数？

MDP建模的例子

基于网格的最短路径问题，具有自然干扰。

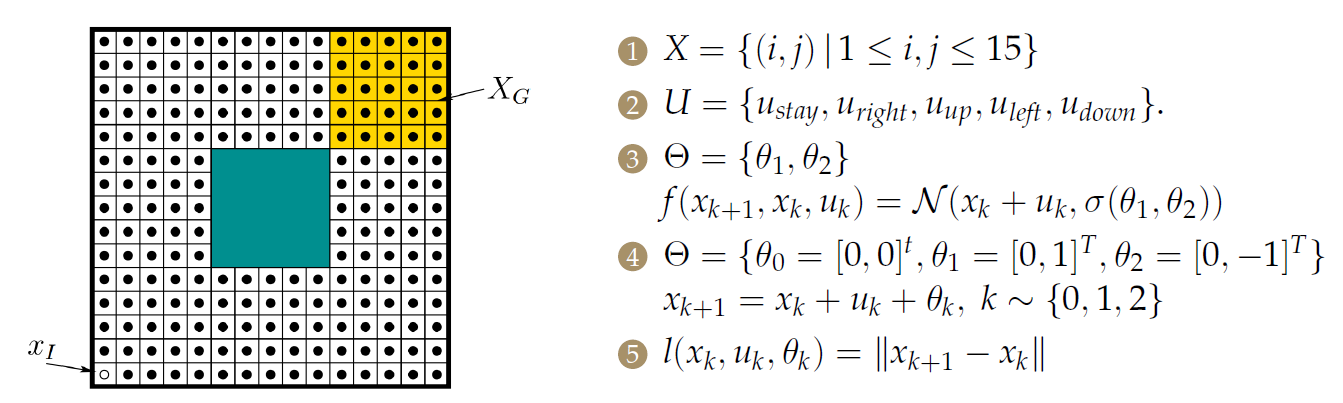
状态空间就是栅格中的点；
动作是四连通（也可以采用八连通）；

自然的动作空间是最难以定义的。

• 第一种：【3】使用连续的方式，定义为机器人位置附近的高斯分布
• 第二种：【4】使用离散的方式，定义规定好的不确定距离。

代价函数简单地定义为两状态之间的距离。

求解上述例子

与之前的path和trajectory具有本质不同，因为存在自然的干扰，因此必须是在执行动作之后，受到干扰到达一个位置，并决策在当前位置下应该采取什么动作（决策树）。

1. 定义plan（计划）：\(\pi:X\rightarrow U\)，其本质是从状态空间到动作空间的映射，决定机器人在某种情况下执行何种动作。

2. 定义轨迹集合：\(\mathcal{H}(\pi,x_s)\)，其表示由\(\pi\)引发的从\(x_s\)开始的轨迹集合。
   一条轨迹即\((\tilde{x},\tilde{u},\tilde{\theta})\in \mathcal{H}(\pi,x_s)\)。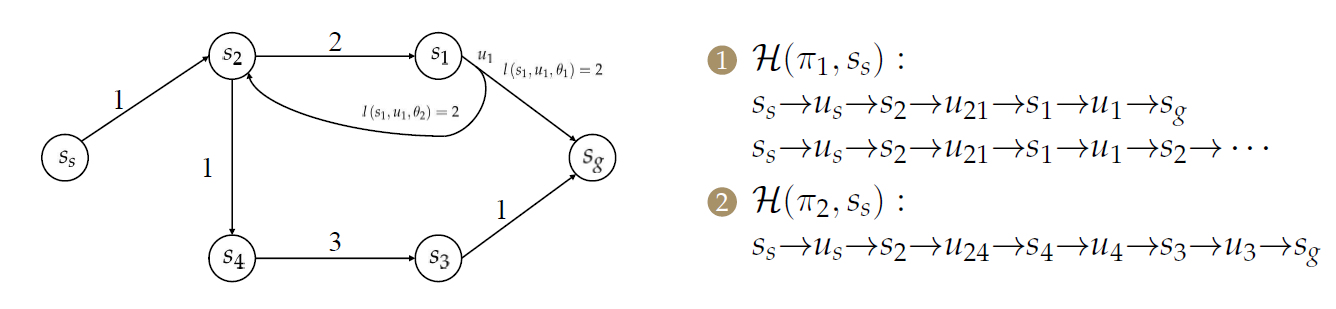

   
   \(\pi_1\)倾向于走路径的上半部分，\(\pi_2\)倾向于走路径的上半部分。

3. 定义代价函数

   定义特定计划\(\pi\)（而不是轨迹）的成本为\(G_{\pi}(x_s)\)：目标成本。用于评估该计划的总体表现。

   1. worst-case
      
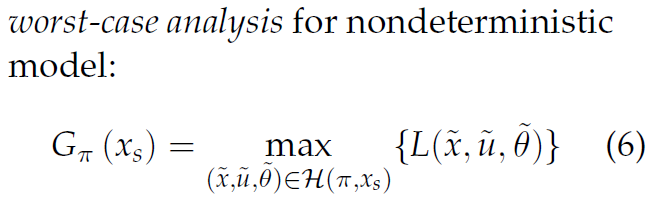
      穷举所有轨迹，寻找最大成本。
   2. expected-case
      
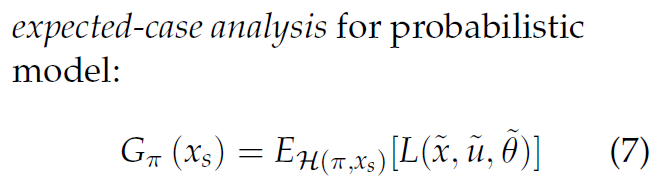
      穷举所有轨迹，计算平均成本。

Minimax Cost Planning

解法

直接求解该问题十分困难（指数爆炸）

使用动态规划的方法，寻找第k步和第k+1步之间的关系。

1. 最终状态\(F\)的最佳目标成本可以直接获得$G^*_F = l_F(x_F)，
2. 从阶段\(K\)到阶段\(F = K + 1\)的所有最优一步计划的成本为
   
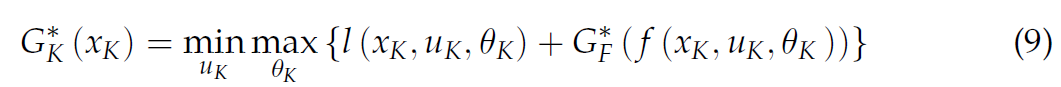
3. 更一般地情况下，给出\(G^*_{k+1}\)时可计算\(G^*_k\)如下：

\[\begin{align} G_{k}^{*}\left(x_{k}\right)=\min _{u_{k}} \max _{\theta_{k}}\left[\min _{u_{k+1} \theta_{k+1}} \cdots \min _{u_{K}} \max _{\theta_{K}}\left(l\left(x_{k}, u_{k}, \theta_{k}\right)+\sum_{i=k+1}^{K} l\left(x_{i}, u_{i}, \theta_{i}\right)+l_{F}\left(x_{F}\right)\right)\right]\tag{10} \\ G_{k}^{*}\left(x_{k}\right)=\min _{u_{k}} \max _{\theta_{k}}[l\left(x_{k}, u_{k}, \theta_{k}\right)+\underbrace{\min _{u_{k+1} \theta_{k+1}} \cdots \min _{u_{K}} \max _{\theta_{K}}\left(\sum_{i=k+1}^{K} l\left(x_{i}, u_{i}, \theta_{i}\right)+l_{F}\left(x_{F}\right)\right)}_{G_{k+1}^{*}\left(x_{k+1}\right)}]\tag{11} \end{align} \]

由此，可以得到动态规划的递归方程：

\[\begin{align} G_{k}^{*}\left(x_{k}\right)=\min _{u_{k} \in U\left(x_{k}\right)}\left\{\max _{\theta_{k} \in \Theta\left(x_{k}, u_{k}\right)}\left\{l\left(x_{k}, u_{k}, \theta_{k}\right)+G_{k+1}^{*}\left(x_{k+1}\right)\right\}\right\} \tag{12} \end{align}\]

示例

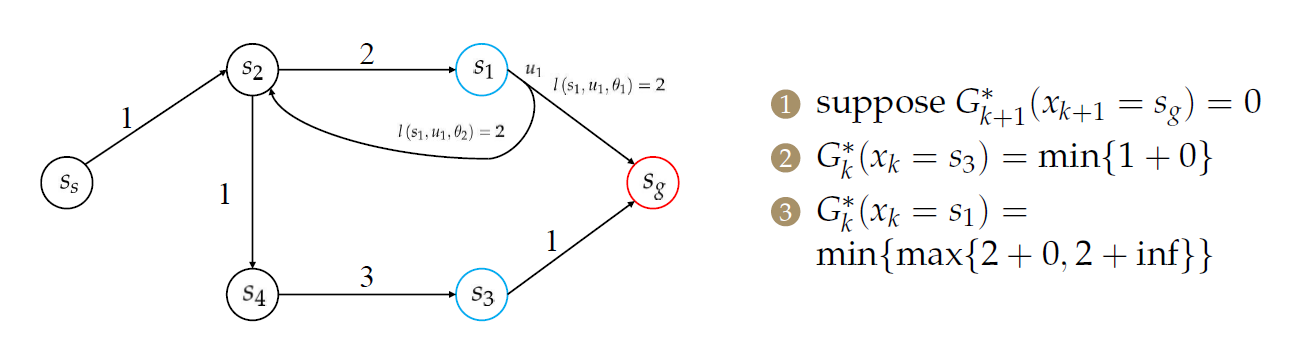
首先假设终点处的cost-to-goal（目标成本）是0，其余点均为\(\infty\)。
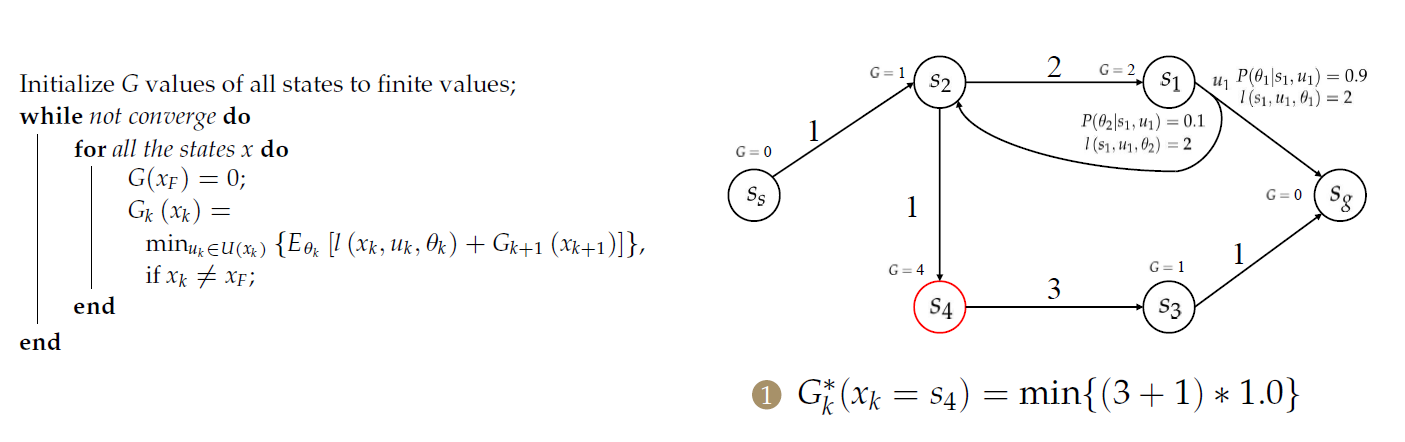
随后，计算\(s_3\)和\(s_1\)的目标成本。

Nondeterministic Dijkstra

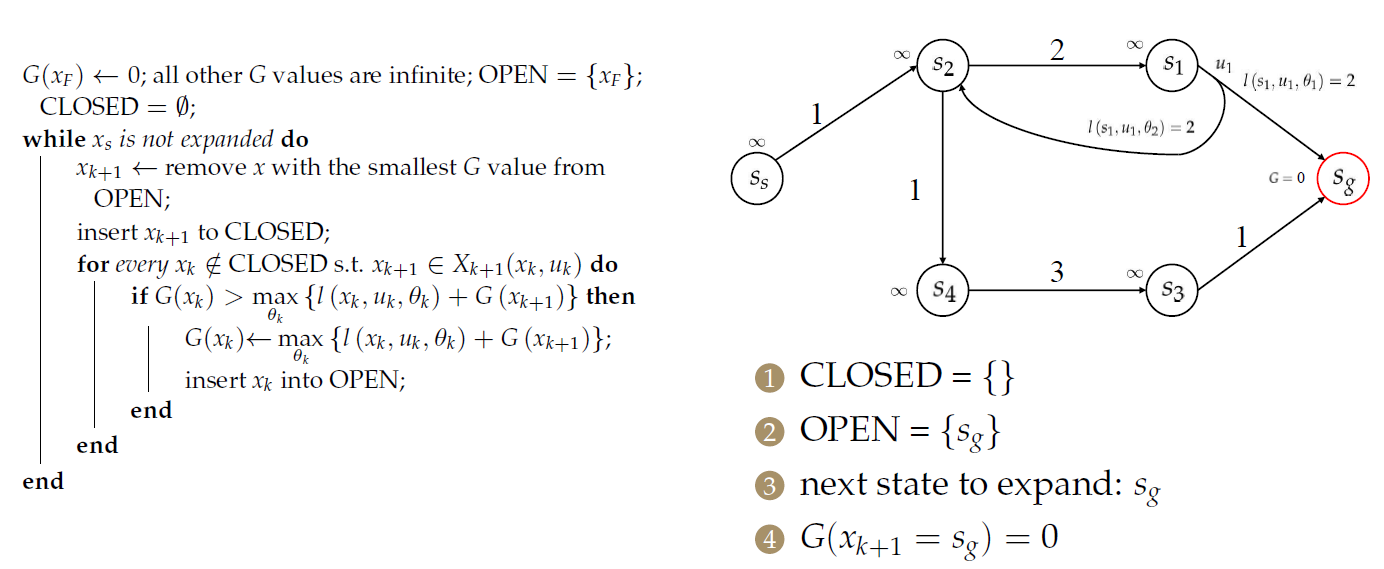
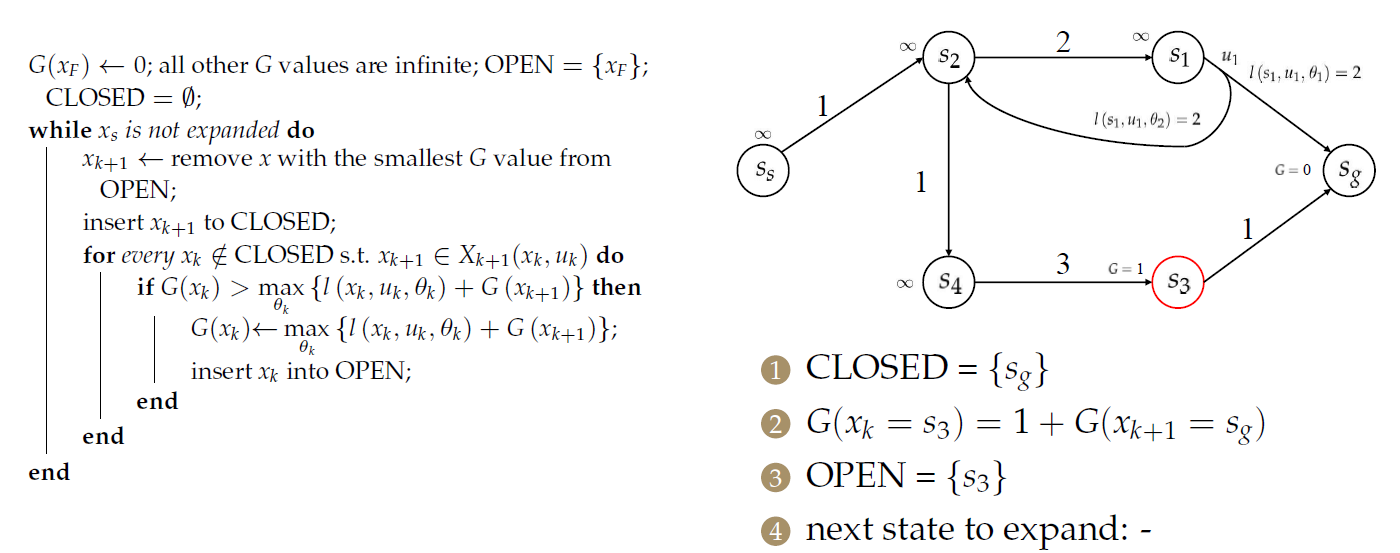
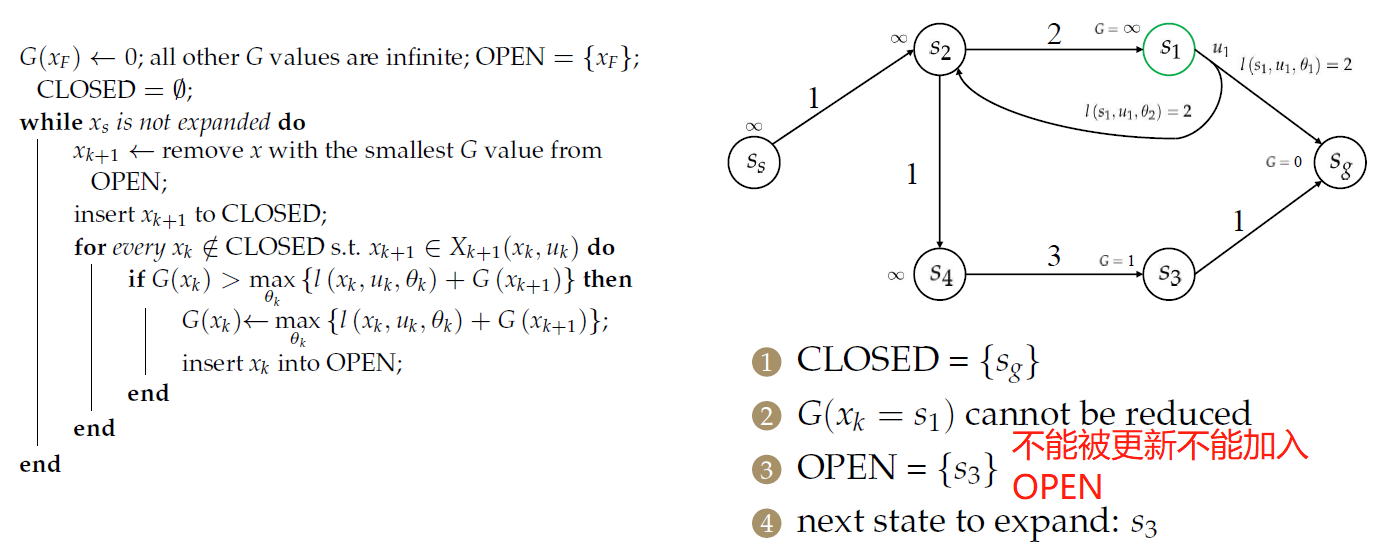
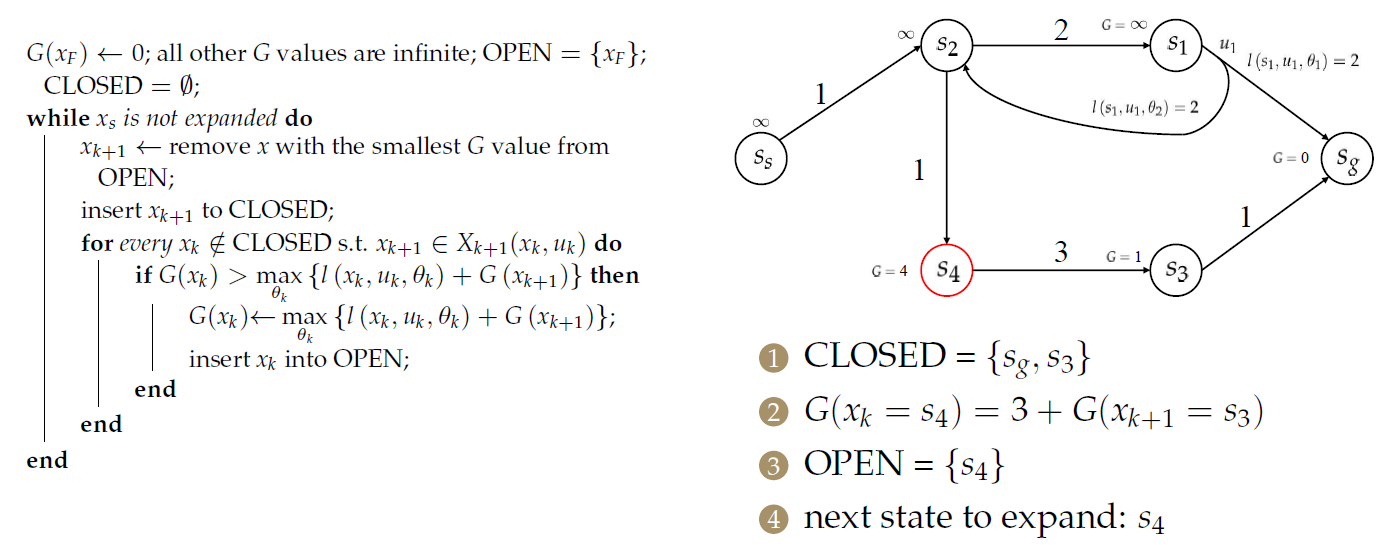
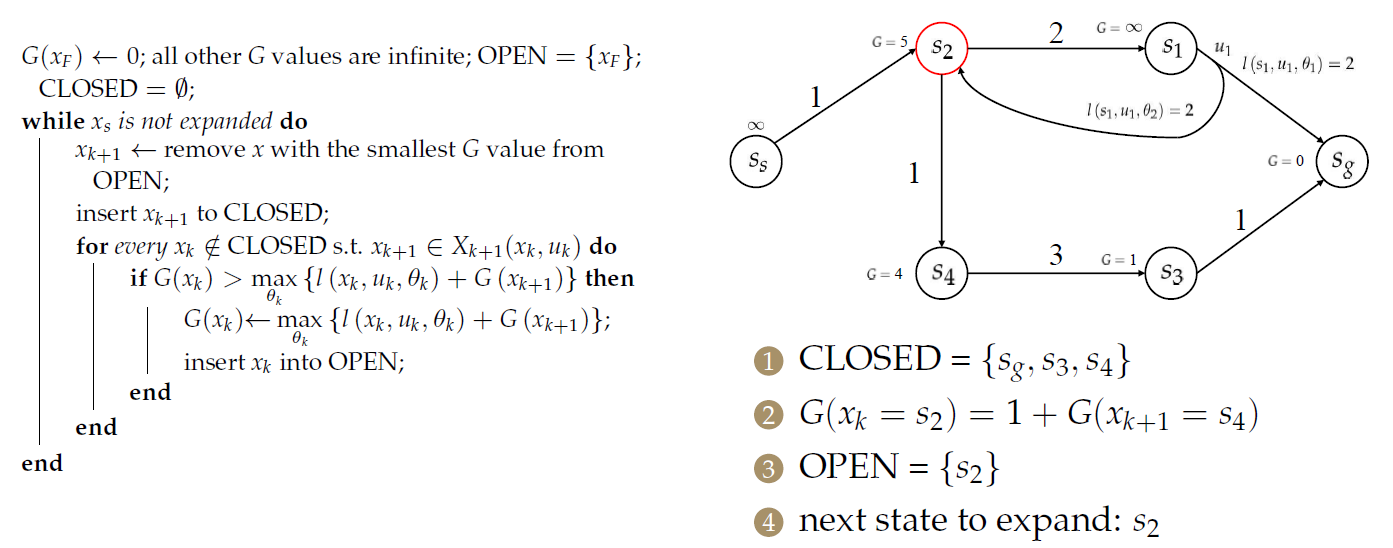
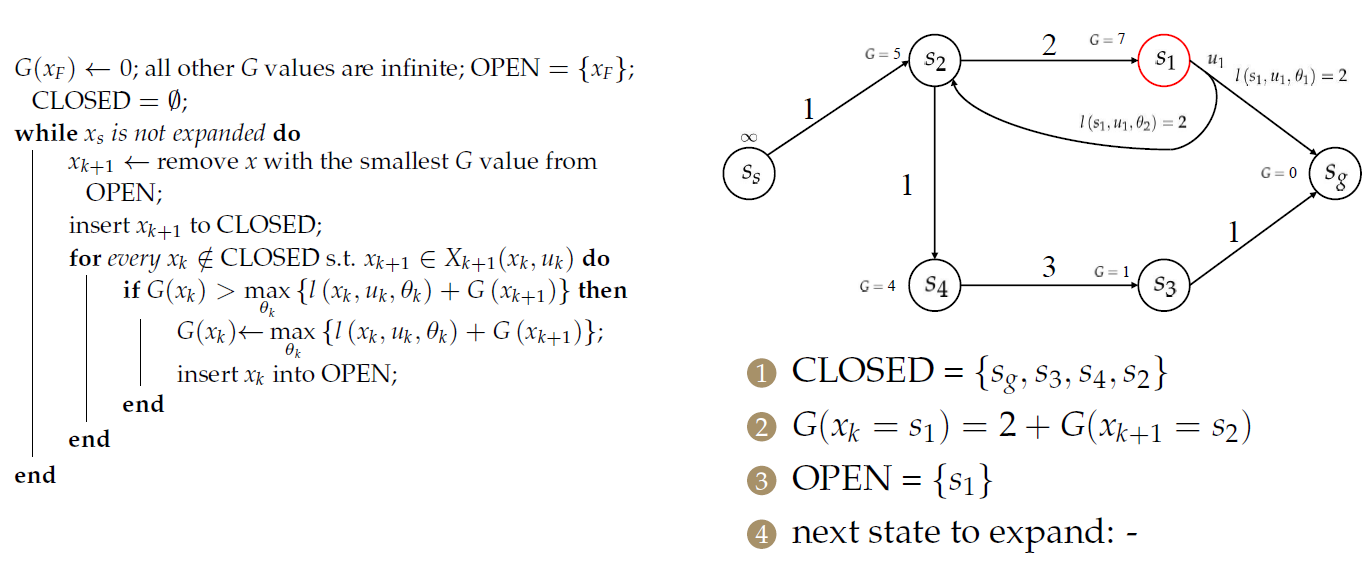
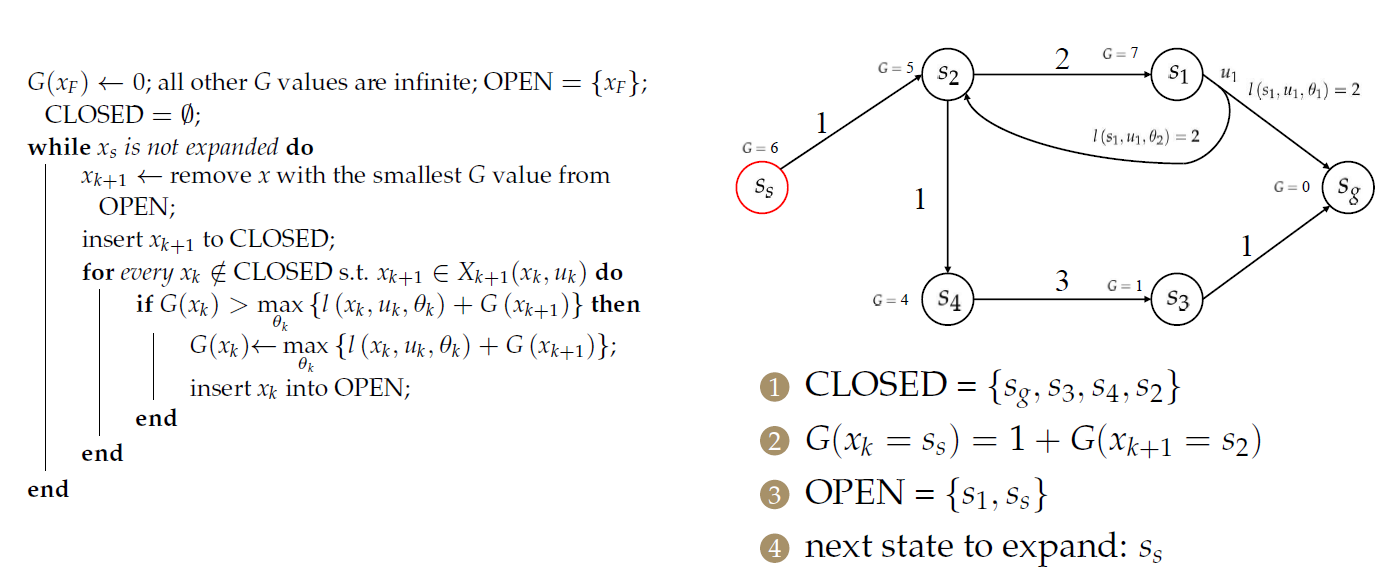
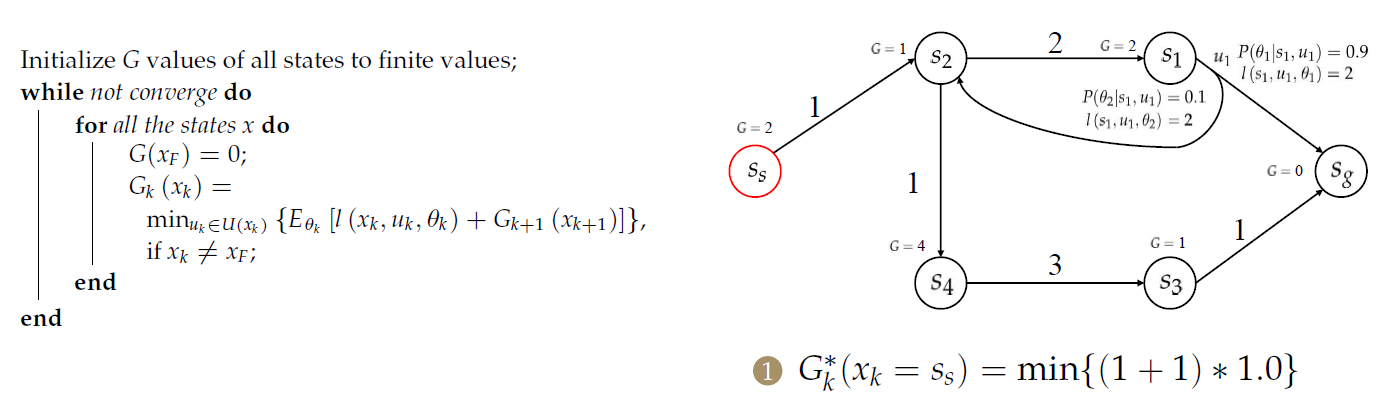
对于\(s_2\)，需要处理2个前序节点：

思考

1. 如何将算法提高到A*？
2. 该算法可以处理失败的情况吗？
   例如，陷入循环怎么办？
3. 如何从中得到最优决策\(\pi^*\)？
   只是更新了节点的目标成本，并没有找到最优决策。

Pros and Cons

• 对不确定性的鲁棒性强
• 算法过于悲观（效率难以保证）
• 比普通路径规划更难计算
  传统路径规划只需要计算一条path，但含有不确定性的路径规划需要计算一个决策树
  • 特别是当不确定性Dijkstra或A*不适用时（只适用于可显式构造出graph的问题，不适用于连续性问题），计算更难
  • 甚至在不确定性Dijkstra或A*适用时，仍然比使用A*计算单个路径还要昂贵。-为什么？

Expected Cost Planning

递归公式

递归公式：

它有一个特殊的名称，叫做Bellman Optimality Equation。（对于MDP/机器学习领域）

例子

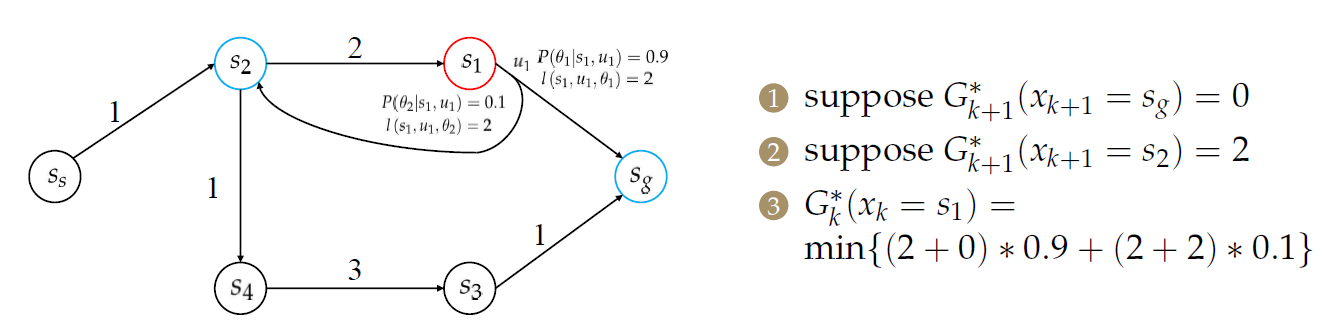
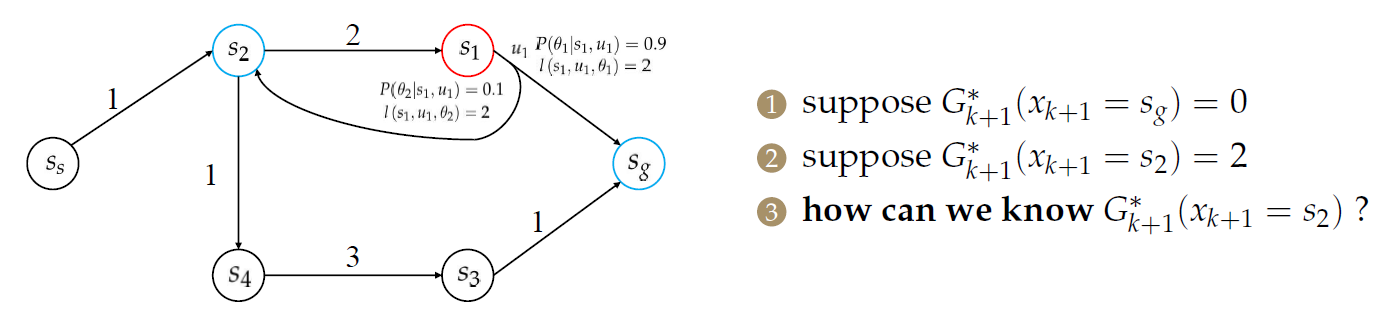
由于存在\(s_1\)到\(s_2\)的回环（导致二者的求解相互依赖），因此我们能否求出\(G^*_{k+1}(x_{k+1}=s_2)\)呢？

怎么解决这种情况？

Value Iteration(VI) 值迭代算法

算法概述

注意与Nondiscrimination的区别是，这里将其初始化为有限值（比较小的值，其值选取影响收敛速度，有很多文献讨论取值方法）
随后运行该算法直到收敛为止。

算法特性

• 通过进行值迭代来获得最佳值。

  • 最优性与迭代顺序无关。
  • 收敛速度取决于迭代顺序。

• Bellman更新方程是实现Bellman最佳方程的一种方法。

算法示例

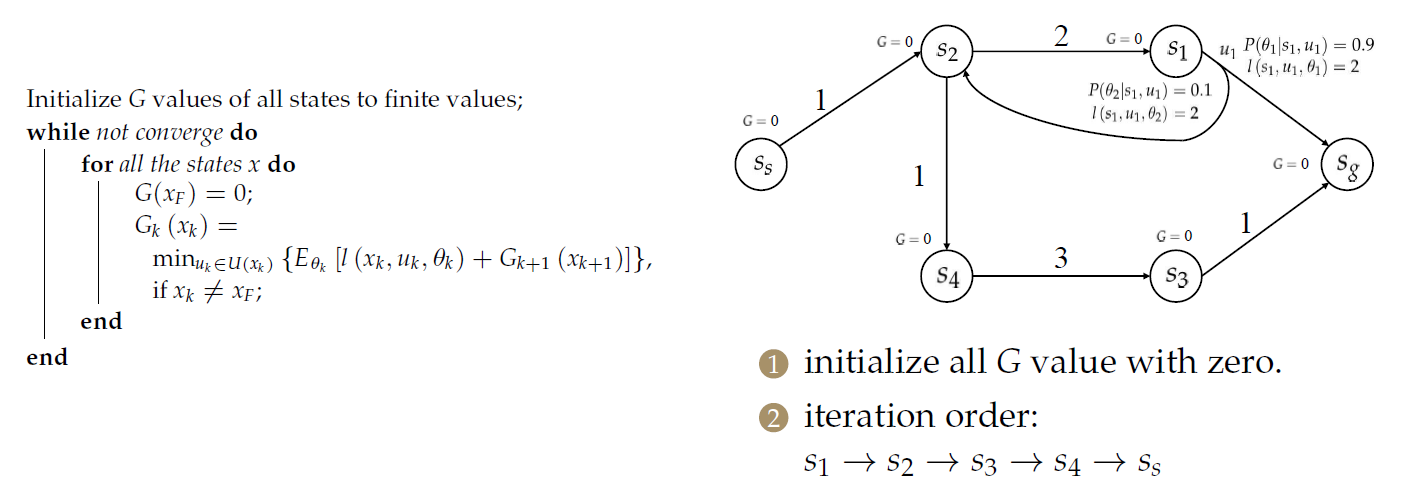
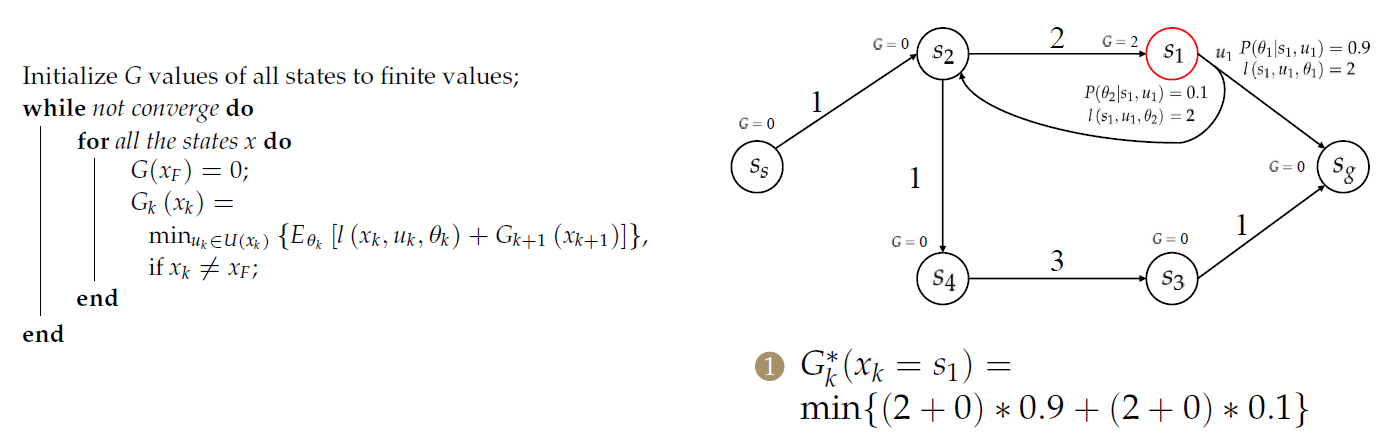
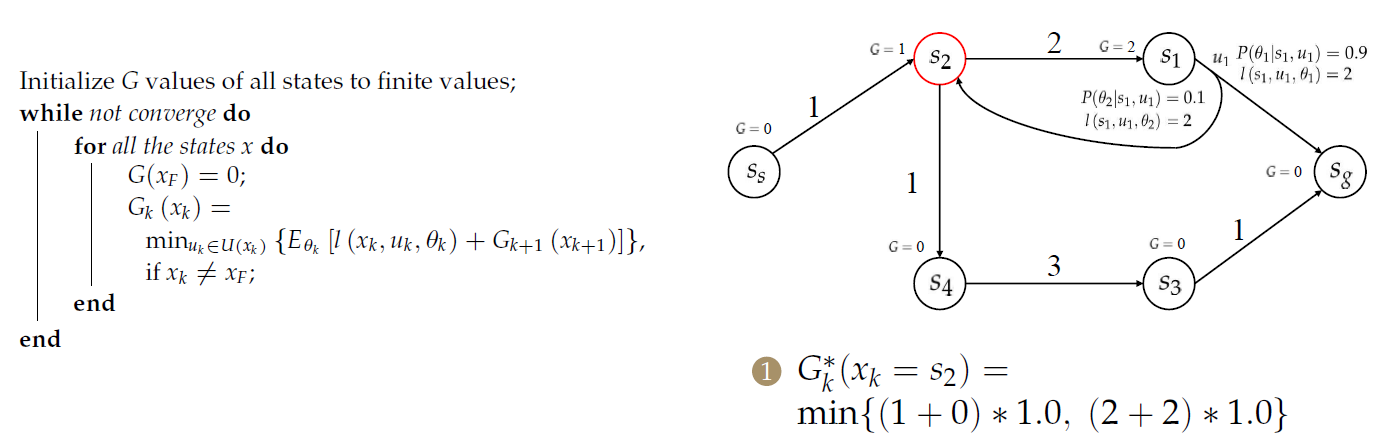
注意\(s_2\)与\(s_1\)情况不同！！！

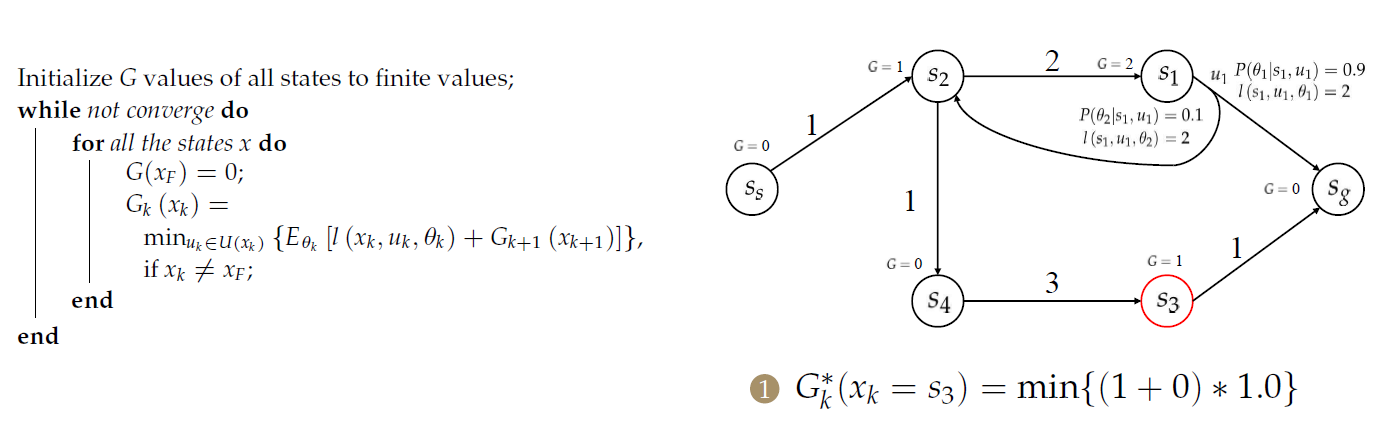
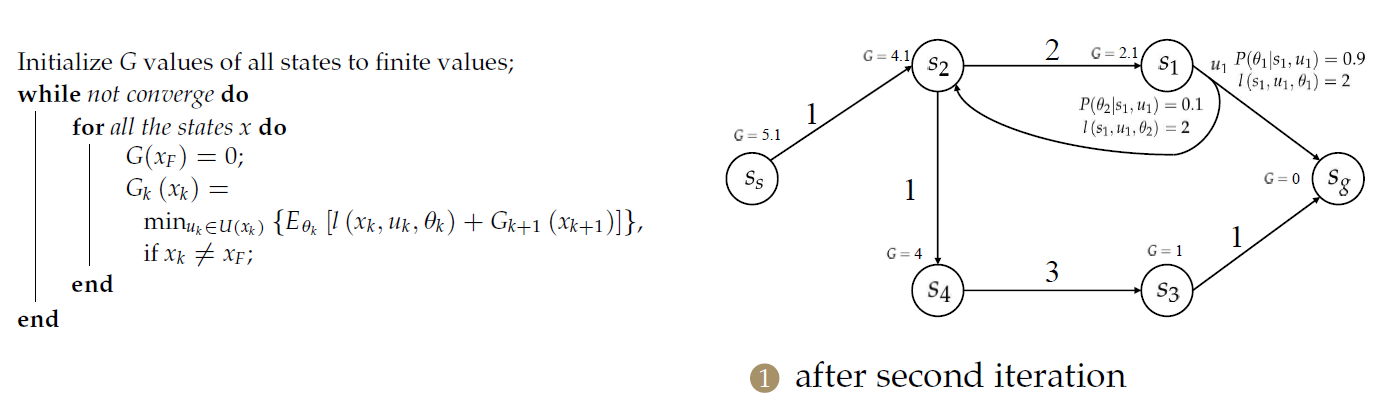
第二次迭代后

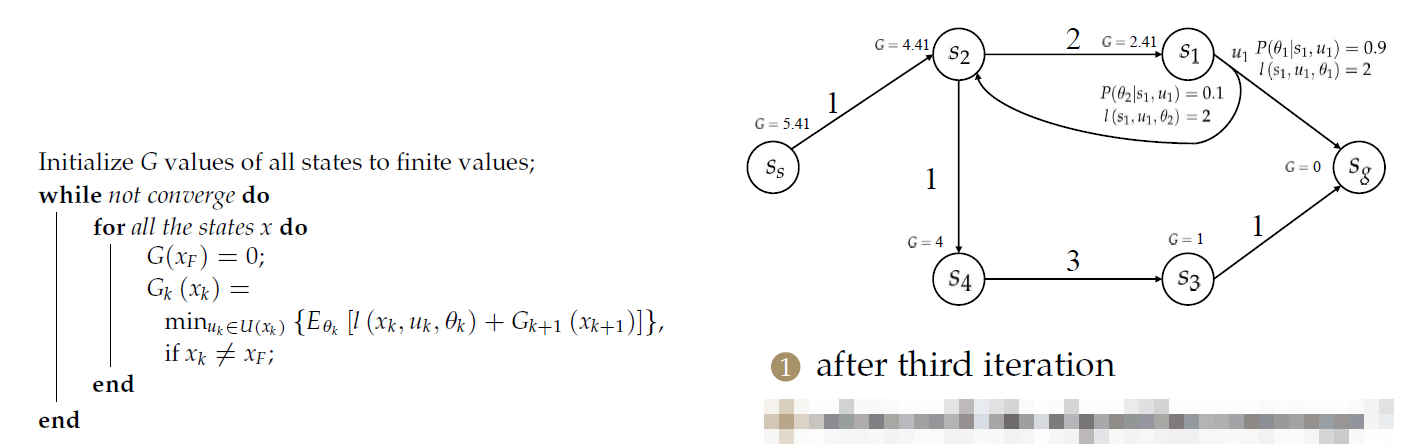
第三次迭代后

思考

• 算法何时收敛？
• 如何改进算法？
• 如何证明收敛？（即通过Bellman更新方程可实现Bellman最佳方程）
• 如何获得最佳的计划\(\pi^*\)？

Pros and Cons

• 概率最优
  • 反映平均表现
  • 特定的执行可能不是最佳的
• 要求不确定性的分布，即定义自然的行动空间，以及定义其如何依赖于机器人的行动空间的（比较困难，也即建模（用MDP表示现实问题）的困难）
• 比普通路径难计算
  • 遍及整个地图（状态）
  • 受初始化和迭代顺序的影响
    如何优化计算有很多地相应研究。

Real Time Dynamic Programming

这是对上一章中Expected Cost Planning的优化算法。

RTDP算法：

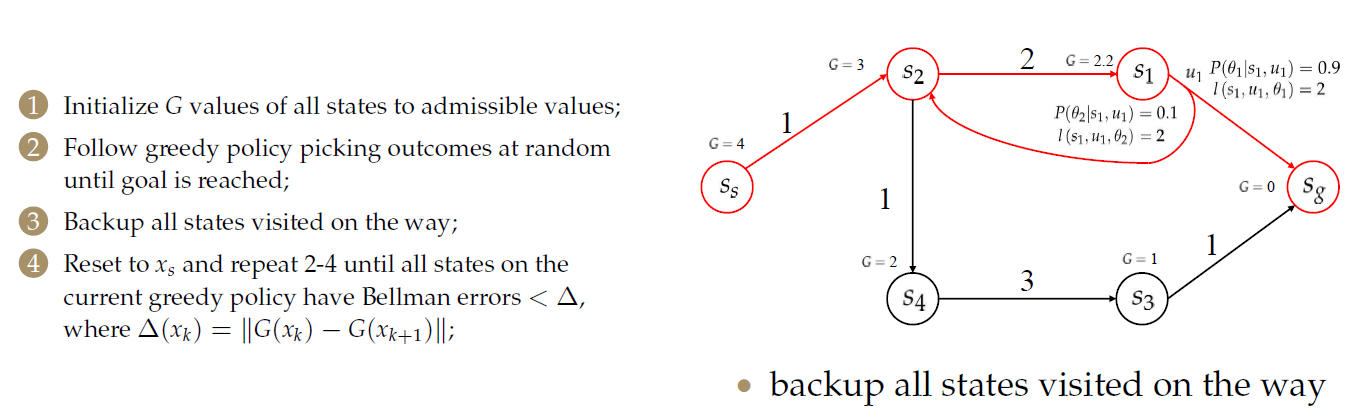
1. 将所有状态的\(G\)值初始化为允许值（admissible，与之前介绍的图搜索算法中启发因子类似，要求其不能大于真实值）；
2. 按照初始化后的\(G\)值，使用贪婪算法选择一个动作，对于代价相等的，采用随机选取的方法，直到达到目标为止；
3. 备份途中访问过的所有状态；
4. 重置为\(x_s\)并重复2-4，直到当前贪婪策略的所有状态都具有贝尔曼误差（Bellman error）<\(Delta\)，其中\(\Delta(x_k)=||G(x_k)-G_{k+1})||\);注意此处的\(x_k\)和\(x_{k+1}\)是指迭代次数而不是迭代中的节点序号。

优点：

• 是非常有效的替代值迭代算法的方法
  • 不计算所有状态的值
  • 集中于相关状态的计算

例子：

初始化的方法：该点到终点边的数量。

贪婪地选择一个动作，直到到达目标。

更新\(G\)值。

重新按贪婪的方法选择：

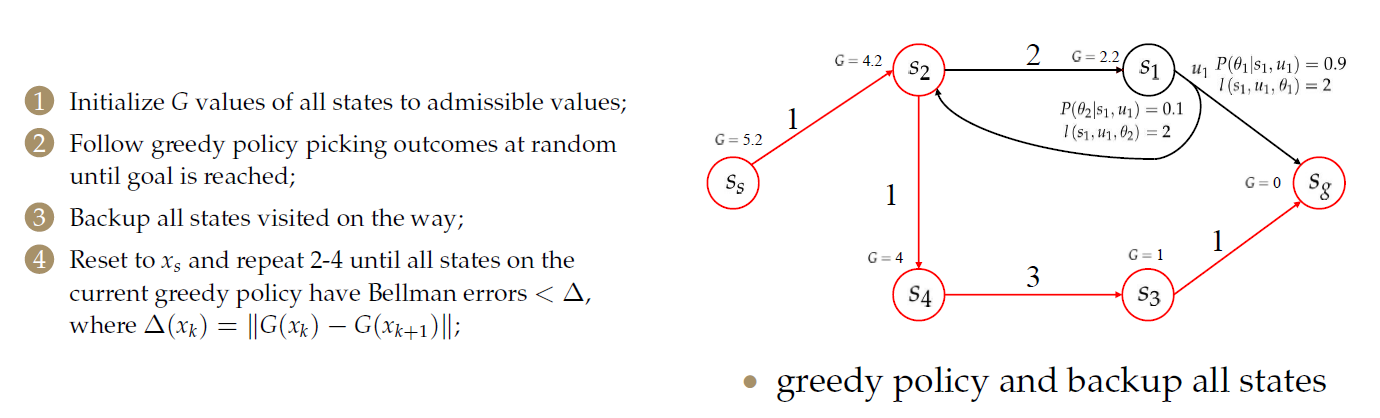
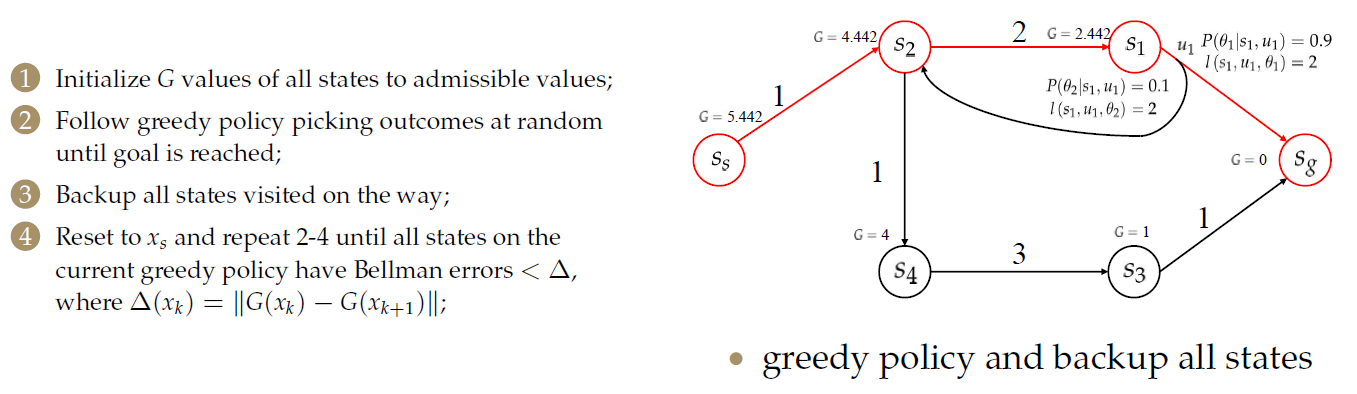
直到满足结束条件。

注意：如果一直按照贪婪的方法选取动作，很可能陷入局部最优或陷入循环，导致不能得到最优结果。
为了解决这一问题，会加入一个随机探索的策略，即有一定的概率去选择非最优的动作。
Exploration & Exploitation问题（MDP/强化学习中的常见问题）

Homework

经典赛车问题：紫色为赛道，蓝色为禁止通行区，绿色为起点，黄色是终点。

汽车的行动空间：控制\(x,y\)两方向的加速度。
自然的行动空间：维持原状态（0.1），成功执行（0.9）。【仅考虑了执行的不确定性，未考虑观测的不确定性等】
单步的代价函数：每执行一个动作代价为-1。

1. 问题建模
2. 如何求解以及求解策略的选择
3. 用RTDP算法解决这一问题

根据提供的值迭代的方法实现的代码，换用RTDP方法实现之。