Motion Planning for Mobile Robots 学习笔记6
Outline
- Introduction
- Soft-constrained Optimization
- Hard-constrained Optimization
- Case Study
- Homework
Introduction
Minimum snap
优点:
- 一定可在某时刻到达某航路点;
- 计算其导数方便;
- 其求解是高效的。
缺点:
仅可控制路标点,无法控制内部轨迹;
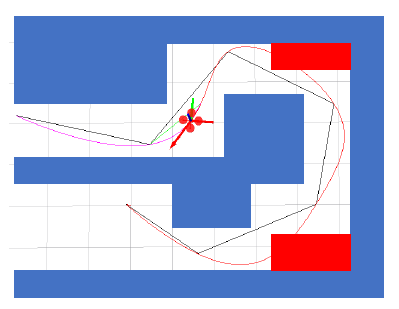
改进方法:
- 加力(Adding forces):软约束
- 加约束(Adding bounds):硬约束
Hard/ Soft constraints
Hard constraints

Soft constraints
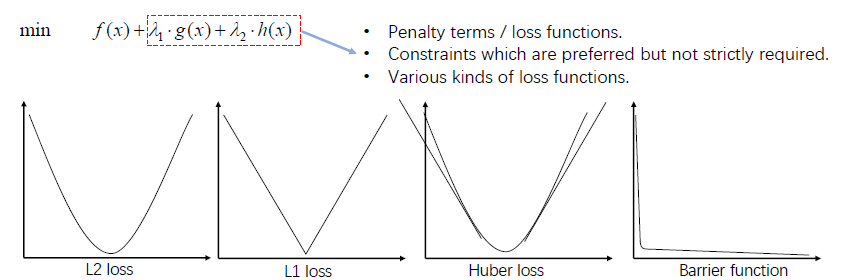
使其倾向于满足约束。
Hard Constraints Optimization
Corridor-based Trajectory Optimization
Online generation of collision-free trajectories for quadrotor flight in unknown cluttered environments. Jing Chen et al.
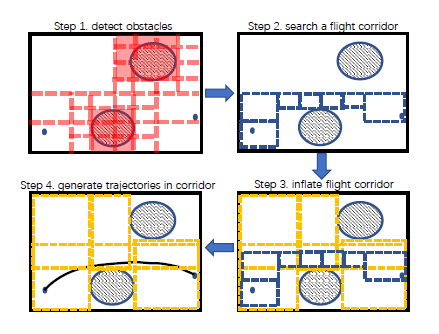
- 探测障碍物,生成八叉树地图
- 搜索出一条可行轨迹,生成飞行走廊
- 膨胀飞行走廊
- 生成分段连续的轨迹
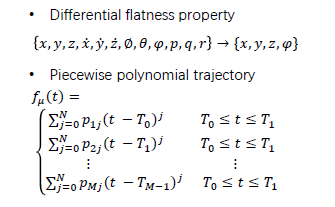

注意:此处没有路径点约束(不要求一定通过确定的点),而是Safety constrains(要求每段轨迹都在飞行走廊内)。
Problem formulation
-
起点终点状态约束

-
过渡点约束
只要求前后轨迹交点在两块区域的相交处
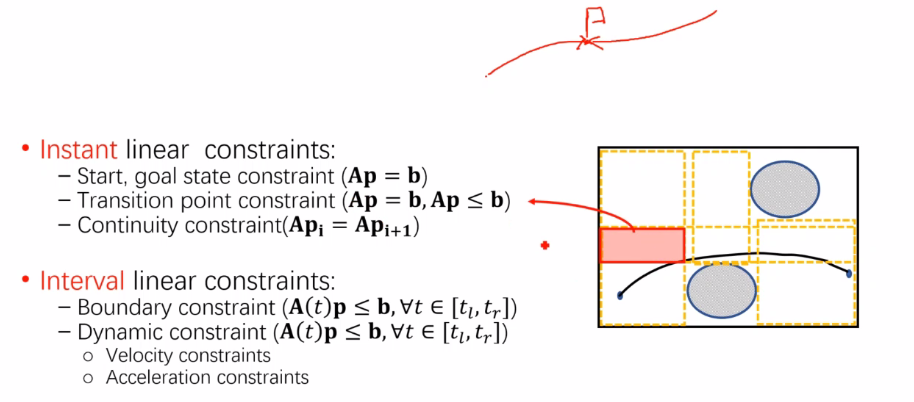
这是由于如果对整段轨迹施加约束,需要离散时刻对每点的横纵坐标进行约束,当凸优化问题具有过多约束时,将难以求解。 -
连续性约束
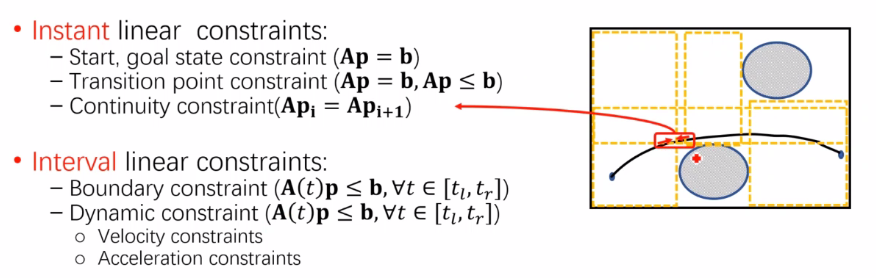
-
避障约束
-
动力学约束
4、5中为避免离散地进行多时刻的检测,选择进行后验的检测。
Advantages
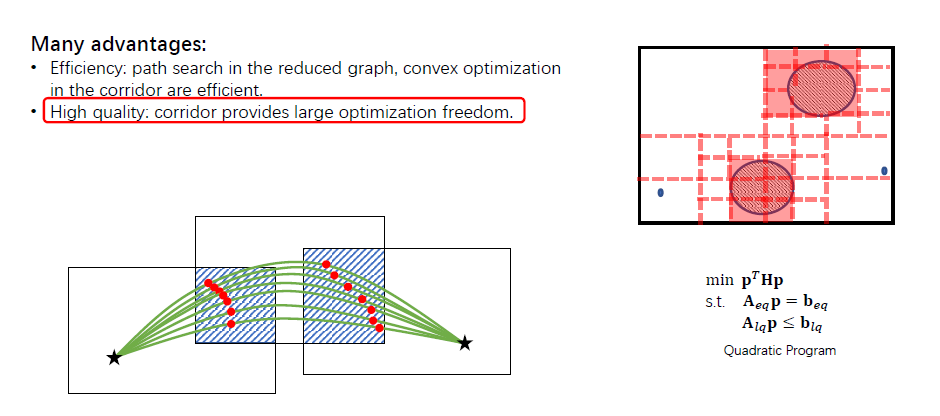
存在一个隐形的时间分配,使之更能生成优化轨迹。
Disadvantage
问题:所有约束仅在分段连接点上强制执行,如何确保它们在所有轨迹上都有效?
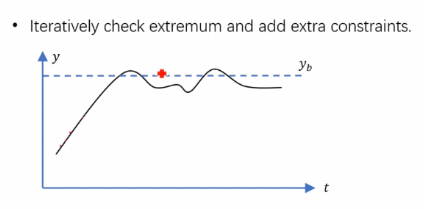
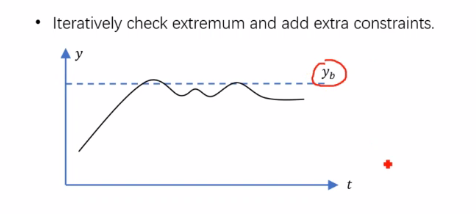
迭代地检查是否全部在飞行走廊内,若否,则施加更多约束以使之在飞行走廊内。
同样地,这种方法也可以施加在速度与加速度约束上。
注意,离散时刻上的约束优化问题很费时间。
另外,多次迭代的方法也浪费计算资源。
在初值不理想时,还有可能无法得到较优轨迹。
如何做到高效在线使用呢?
Bezier Curve Optimization
使用伯恩斯坦多项式来替代普通多项式。
Bézier曲线
贝塞尔曲线只是一个特殊的多项式,可以通过以下方式将其映射为普通多项式\(p=M\cdot c\),因此所有先前的(对普通多项式的)推导仍然成立。
Bezier曲线属性
- 控制点与曲线:贝塞尔曲线始终在第一个控制点开始,在最后一个控制点结束,并且从不通过任何其他控制点
- 凸包:贝塞尔曲线B(t)由一组控制点ci组成,这些控制点ci完全限制在所有这些控制点Hodograph定义的凸包内。
- 导数:贝塞尔曲线B(t)的导数曲线B'(t)称为Hodograph。它也是一条贝塞尔曲线,控制点由n。(c-c)定义,其中n是固定时间间隔的度数。
- 时间:贝塞尔曲线总是在[0.1]之间,可以对时间进行映射。
如何使用凸包性质?
使用凸包性质使轨迹在飞行走廊内生成。
甚至可以将速度与加速度限制在一定范围内。(上下限)
Trajectory Generation Formulation
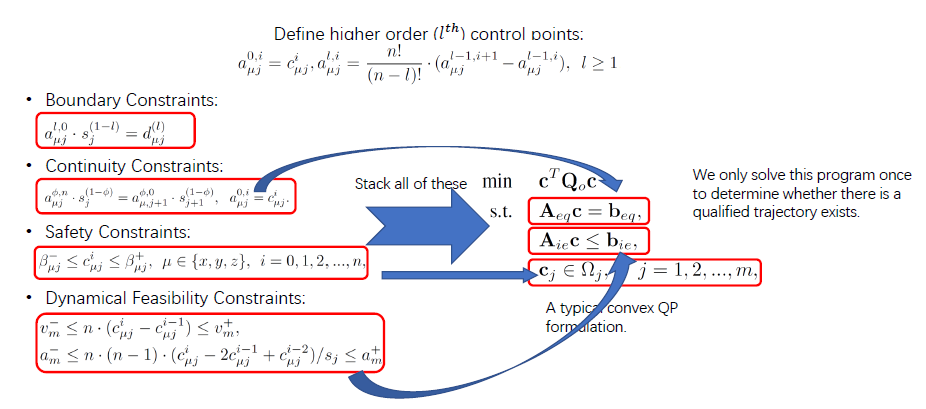
Online Safe Trajectory Generation For Quadrotors Using Fast Marching Method and Bernstein Basis Polynomial, Fei Gao et al.
Source code released at https://github. com/HKUST-Aerial-Robotics/Btraj A complete UAV online motion planning framework
Other Options
Dense constraints(密集约束)
A hybrid method for online trajectory planning of mobile robots in cluttered environments, L Campos-Macias et. al
- 环境按照需生成的飞行走廊尺寸进行膨胀
- 寻找一条路径
- 在路径点上生成走廊(由于已膨胀障碍物,故肯定可找到走廊)
- 在每个走廊格内,机器人以恒定加速度运动
- 推导出满足要求的加速度值(详见论文)
问题:机器人速度不高。
Mixed integer optimization(混合整数优化)
Mixed-integer quadratic program trajectory generation for heterogeneous quadrotor teams, D. Mellinger et al.
注意:常用的避障约束条件\(||P-P_o||>d\)这个条件并不是凸的。
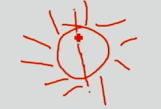
如何保持其凸性质呢?
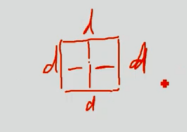
施加一个方形的约束。
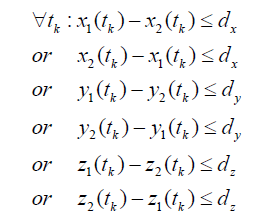
(或的关系)
使用“Big M”法将其转换为
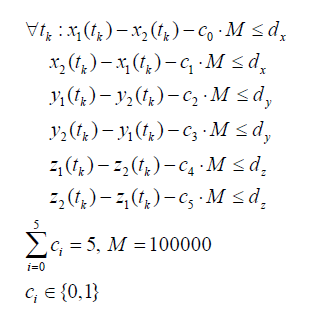
(与的关系)
注意:MIQP(Mixed-integer QP)问题的求解效率不高。其复杂度随着整数变量的增加指数爆炸式增长。
此方法提出是多无人机编队使用的。在单个机器人避障时,并无必要使用此方法。
Soft-constrained Optimization
Distance-based Trajectory Optimization
Motivation
硬约束:
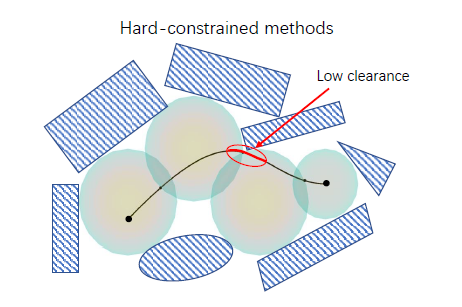
Treat all free space equally(解空间中各点等价,以至于所生成的轨迹可能离障碍物较近。)
Solution space is sensitive to noise(对噪声敏感)
而对于基于视觉的轨迹规划:
Vison-based drone:
Limited sensing range and quality(视觉的距离与质量受限)
Noisy depth estimation(噪声影响严重,影响飞行走廊质量)
软约束:
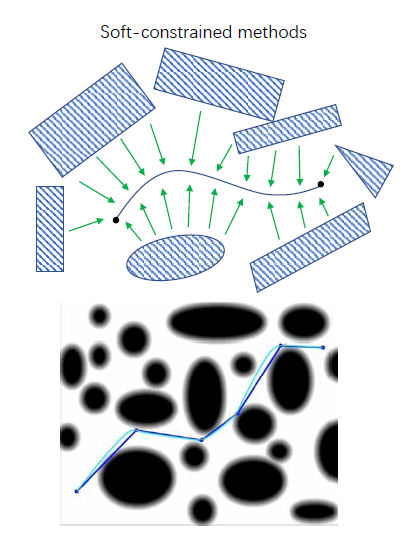
当目标函数设计不合理时,可能部分约束条件无法被满足,这是软约束的一大问题。
Problem formulation

Collision cost:
使用距离场地图(ESDF等)
为什么要对曲线进行积分?
若对时间积分,则积分大小与机器人运动时的速度有关。原因是对时间积分时,为减少积分值,将会使得机器人的通过时间变短,这显然不符合我们的预期。(不是希望在接近障碍物时提高速度,而是希望远离障碍物)
此项无法进行解析求解(如Smoothness cost),因此必须进行数值求解。
注意:此问题不是一个凸优化问题。
原因:距离场(如ESDF)不是凸的。
只能使用非线性优化的方法进行求解。
求解各项导数:
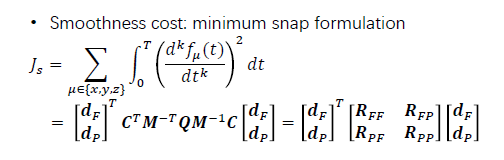
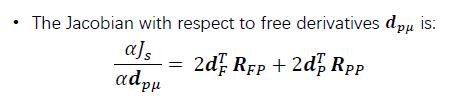


二阶导数不一定要用到。
Euclidean signed distance field(ESDF)

速度与加速度约束类似。
Numeriacal optimization

使得其梯度趋近于0。

注意:给定的初值会影响其最后收敛的最优解。
Line search types
搜索步长设置

最理想状态:往目标函数值下降的方向搜索,选择使其下降最多的步长。
但这种方法不易实施。
一般地,使用最初预设的步长,若函数值下降,则使用该步长。若函数值上升,采用二分法缩短步长。
Gradient descent method
导数下降方法

Newton method
牛顿法

应用于最小二乘问题时,可使用高斯牛顿法。
Levenberg-Marquardt method
一阶二阶结合法

优化方法不是关注重点。
Planning Strategy
Receding horizon re-planning
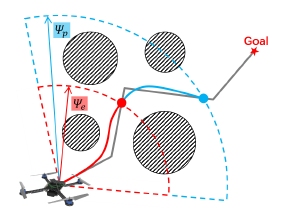
前端:全局路径
局部视野中观测是否需要重新搜索
随后进行后端优化
运动结束后再进行重规划。
Exploration strategy
当映射模块中的异常值阻止时激活。
在附近区域生成安全但短的轨迹。(探索)
悬停观察。
初值选取
一种方法是使用前端的直线path,其优点是无碰撞的,但其缺点在smooth性太差。
另一种方法是使用minimum snap方法先生成一个较光滑的估计,其缺点是安全性不够。
Two-step optimization
先考虑避障的效果,
再进行其他优化
Source code released at
https://github.com/HKUST-Aerial-Robotics/qrad_traj_optimization
A tool for local UAV trajectory optimization Gradient-Based Online Safe Trajectory Generation for Quadrotor Flight in Complex Environments, Foi Gao et al.
Case study
Fast Planner
Framework
Kinodynamic path searching
- B-Spline trajectory optimization
- time adjustment
B-spline trajectory optimization
Hybrid A*生成初始path
Gradient-Based Online Safe Trajectory Generation for Quadrotor Flight in Complex Environments, Fei Gao et al.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号