Motion Planning for Mobile Robots 学习笔记5
Outline
- Introduction
- Minimum Snap Optimization
- Closed-form Solution to Minimum Snap
- Implementation Details
- Homework
Introduction
为什么要平滑轨迹
- 适合自主移动。
- 速度/高阶动力学不能立即改变。
- 机器人不应转弯停止。
- 节约能源。
为什么需要轨迹生成/优化
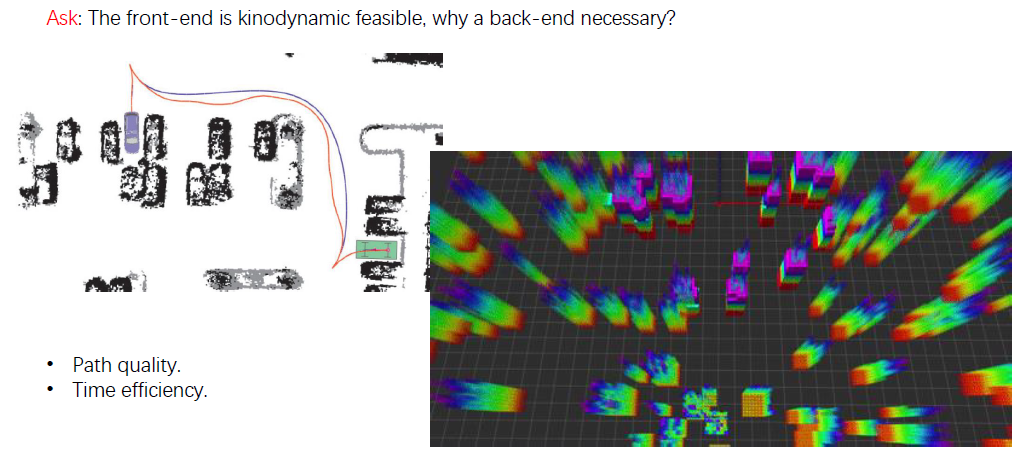
轨迹优化后可以获得更好的轨迹
问题描述
- Boundary condition:
start, goal positions (orientations)
起点终点的边界条件 - Intermediate condition: waypoint positions (orientations)
路径点
- Waypoints can be found by path planning (A *, RRT *, etc.)
- Introduced in previous 3 lectures - Smoothness criteria
评价标准
- Generally translates into minimizing rate of change of "input"
Minimum Snap Optimization
Differential Flatness(微分平坦)
四旋翼的状态和输入可以写为四个精心选择的平面输出及其导数的代数函数。
对于无人机:Minimum Snap Trajectory Generation and Control for Quadrotors, Daniel Mellinger and Vijay Kumar
Quadrotor dynamics


Minimum-snap
Smooth 1D Trajectory

注意:光滑与连续不一样,光滑代表可导。例如,加速度连续可保证速度与位置可导。

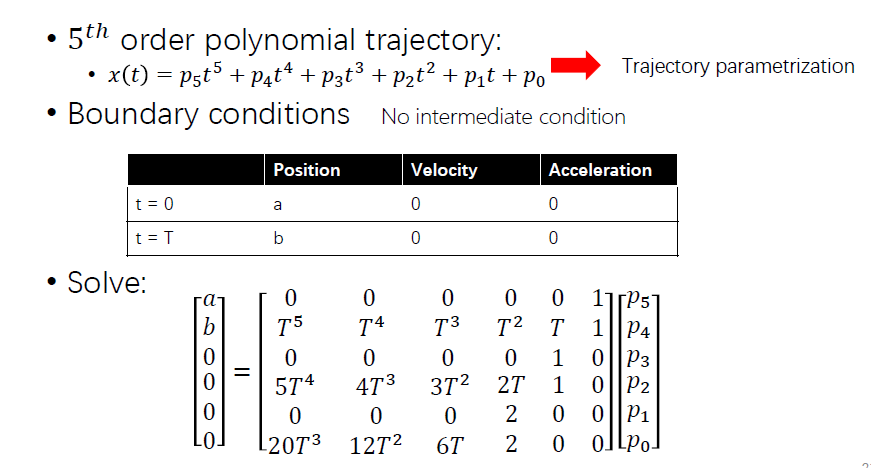
代入末尾条件,直接求解。
Smooth Multi-Segment Trajectory
- 平滑直线段的角。
- 首选恒速运动。
- 首选零加速度。
- 需要对短段进行特殊处理。
Optimization-based Trajectory Generation
Minimum jerk: minimize angular velocity, good for visual tracking
等于最小化角速度(最小化视差变化)
Minimum snap: minimize differential thrust, saves energy
等于最小化推力变化(最优能量)
注:snap是jerk的导数
Minimum Snap Trajectory Generation

注意:必须知道每个分段的持续时间,这里的时间不能求得最优。
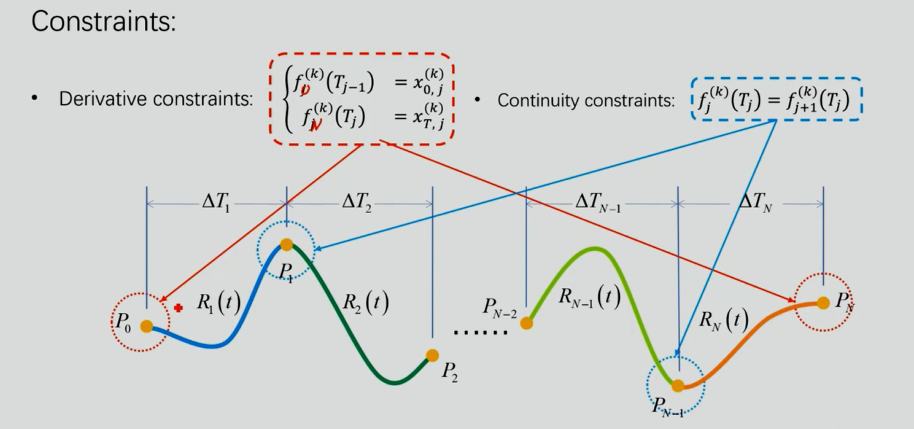
怎么选择轨迹的阶数?
- 确保轨迹几阶光滑
- 确保轨迹几阶连续
- 最小化轨迹的几阶导数(acceleration? jerk? snap?)
工程上:
单段时:
Minimum jerk:N=23-1=5
默认每段轨迹的位置、速度、加速度连续,起点与终点加起来总共是6个未知量,因此选取5次多项式,至少给出6个自由度才可求解。
Minumum snap:N=24-1=7
多段时:
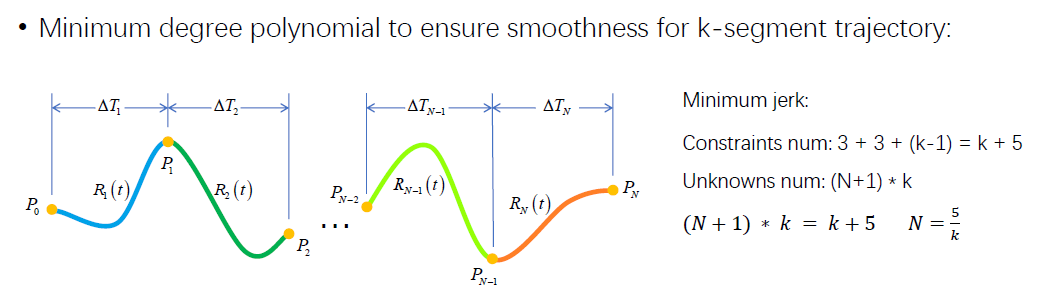
轨迹段数越多,那么所提供的每段轨迹的阶次可以越低。
一般按照最差情况取,即保证只有一段轨迹的情况下也能求解。
时间轴

每段轨迹的cost


这是一个二次型。
每段轨迹的约束
边界值:


连续性:

进行合成:

这是一个二次优化问题(QP)
Convex Optimization
Courtesy: Convex Optimization, Daniel Palomar, HKUST
凸函数
两点间的函数值一定小于这两点值的加权平均。
凸函数基于梯度可以得到全局最优值。
凸集合

凸优化

\(f_0(x)\)、\(f_i(x)\le 0\)是凸函数;
\(A\)是affine形式。
规格严明的凸优化问题解法

Closed-form Solution to Minimum Snap
优化变量的映射
多项式轨迹的直接优化在数值上不稳定,因为多项式系数是没有物理意义的,无法保证其不会为奇异值。
最好使用变量更改为优化每段端点导数,使之成为有实际意义的点。
我们有\(M_jp_j=d_j\),其中\(M_j\)是将多项式系数映射到导数的映射矩阵。
其中:
\(d_j\)是顺序排布的各点的各阶导数;
\(p_j\)是各系数。
映射矩阵怎么写?

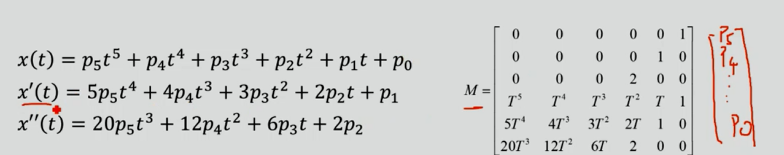
Polynomial Trajectory Planning for Aggressive Quadrotor Flight in Dense Indoor Environments, Charles Richter, Adam Bry, and Nicholas Roy
分解要优化的变量与固定不变的变量
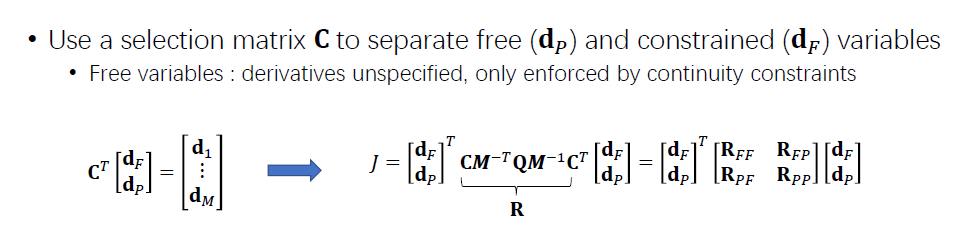
由于决策变量是分开的,R也可以分块。
注意:J只是一个目标函数,而在此处,其约束条件已经被放入了J之中。
边界约束:√
连续性约束:在c矩阵处理中,将某一个变量映射到两段的变量上去。
变成了无约束的二次优化问题,可以:
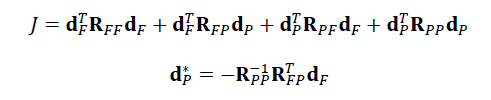
将J展开,随后对\(d_p\)求偏导(\(d_p\)是要优化的量),令导数为0,求出\(d_P^*\)即可。
建立选择矩阵\(c\)
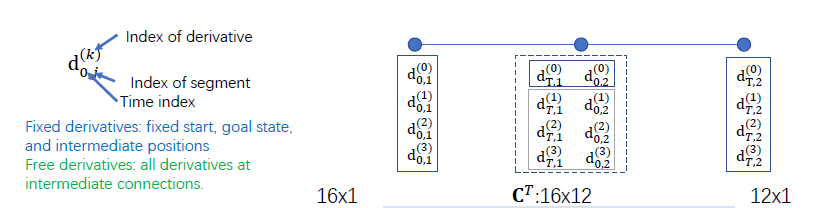
由于中间的8个变量是重复的,因此右侧的变量只有16-4=12个。
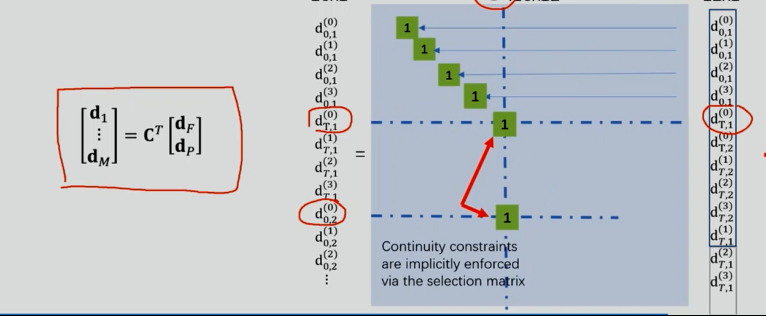
\(c\)的构造方法在于,对于其已由约束固定的变量,直接确定其值;
对于其需满足连续性的变量,设计\(c\)的元素使得其对应同一个值。
注意:使用闭式解得到的结果与使用凸优化数值解法得到的结果是一样的。(要求轨迹阶数一致、每段时间一致)
Hierarchical approach(层次式方法)
path planning + trajectory generation
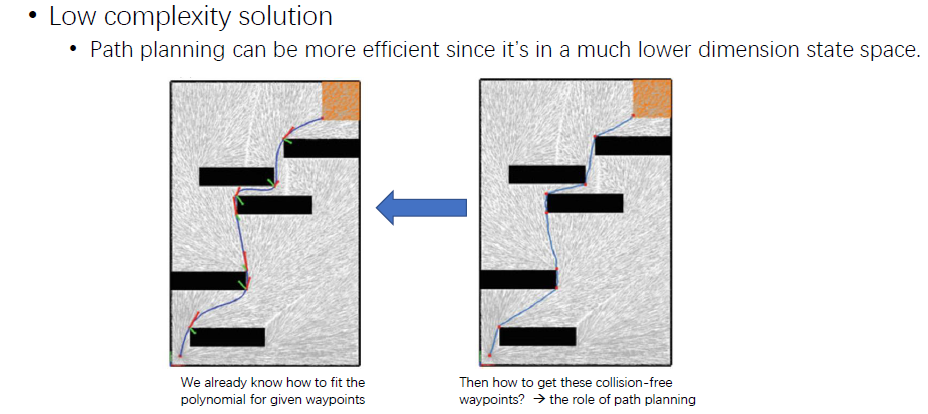
问题:轨迹的安全问题
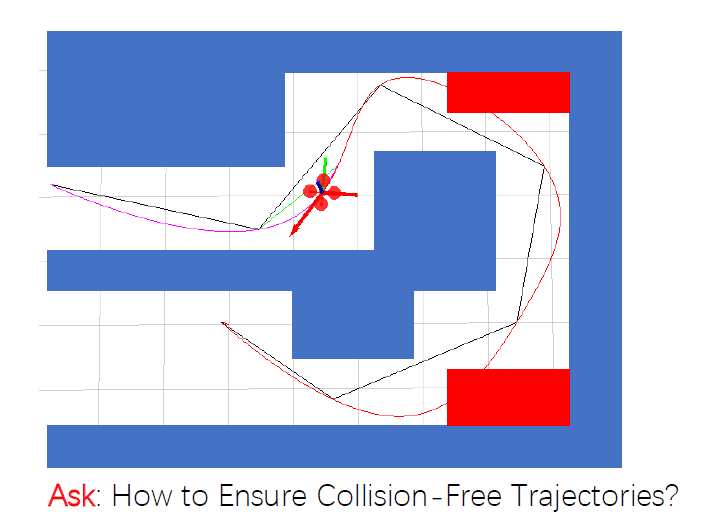
解法:Iterative approach(迭代方法)
初始路径无碰撞。
我们可以迭代地找到轨迹的路径。
这是通过(迭代地)添加中间航路点来完成的。
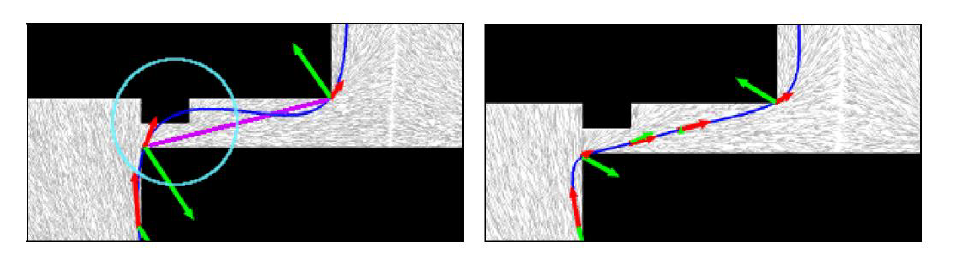
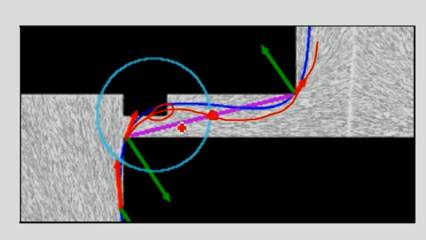

使轨迹逐步逼近于绝对安全的前端路径。
但一开始不加过多点的意义在于提高轨迹质量。
Better Solution?(有没有更好的方法)
- 迭代的加点需要很多次
- 无法保证有限次的加点可以解决这一问题
- 导致局部轨迹质量下降很快
更好的方法是软/硬约束下的轨迹优化
Implementation Details(实践细节)
Convex Solver

Numerical Stability(数值稳定性)
Time normalization(时间归一化)
一些非常小的持续时间可能会完全破坏稳定性。
将短持续时间缩放为正常数字(1.0)。
或在所有曲线上添加比例因子。
Problem scale normalization(空间归一化)
如果问题是大型场景的根本原因。
例如x = 100.0 m的航路点考虑解决一个小问题(沙箱),然后将解决方案重新缩放。
这两个操作在实践中大大提高了数值稳定性。
Other engineering stuff
是否可以独立求解每个轴?
取决于具体情况。
通常情况下,解决3个小范围的问题要比1个大问题更好(稳定,更快)。耦合生成可能会在3个轴上添加不同的权重。
闭式解方法是否一定更好?
闭式解涉及矩阵求逆的问题。计算的鲁棒性与效率都不够好。
多项式函数是否总是可以完成所有问题?
几乎,但不是全部。
一般地,如果计算的\(J=\int|{\rm input}|^2dt\)的情况下,最优轨迹的确为多项式。
但对于\(J=\int(\omega_1J_1+\omega_2J_2)dt\),其最优轨迹并不是多项式,多项式是其退化的形式。但一般可以忽略。
Time Allocation(时间分配问题)
Problem Definition
分段轨迹取决于分段时间分配。
时间分配会严重影响最终轨迹。
如何获得适当的时间分配?
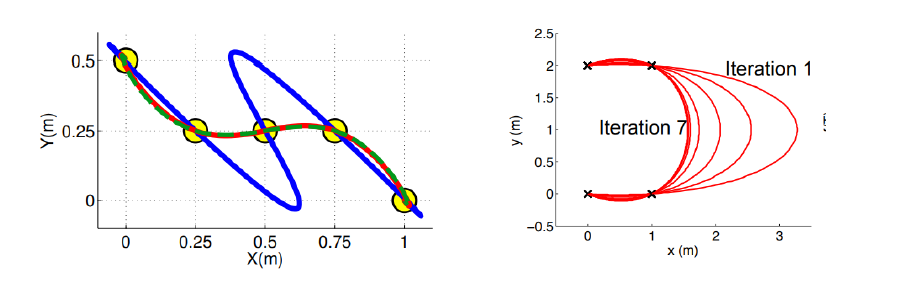
不同时间分配下的轨迹
Naive solution
使用“梯形速度”时间曲线来获取每块的持续时间。
假设每块都加速到最大速度,最后减至0。
使用预期的平均速度来获取每块的持续时间。

但是这种方法:
Far away from optimal.
Only get conservative time profile.
Has no reaction to environmental styles
Online generation of collsion-free trajectories for quadrotor flight in unknown cluttered environments, ]. Chen, ICRA 2016
Fast, dynamic trajectory planning for a dynamically stable mobile robot, M. Shomin, IROS 2014
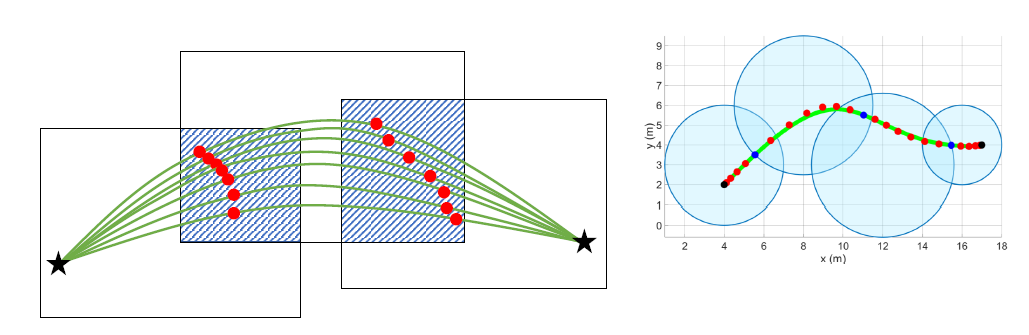
对于使用走廊约束的情况下,有一定的时间调节能力。
Iterative numerical solution
在目标函数中加入时间代价
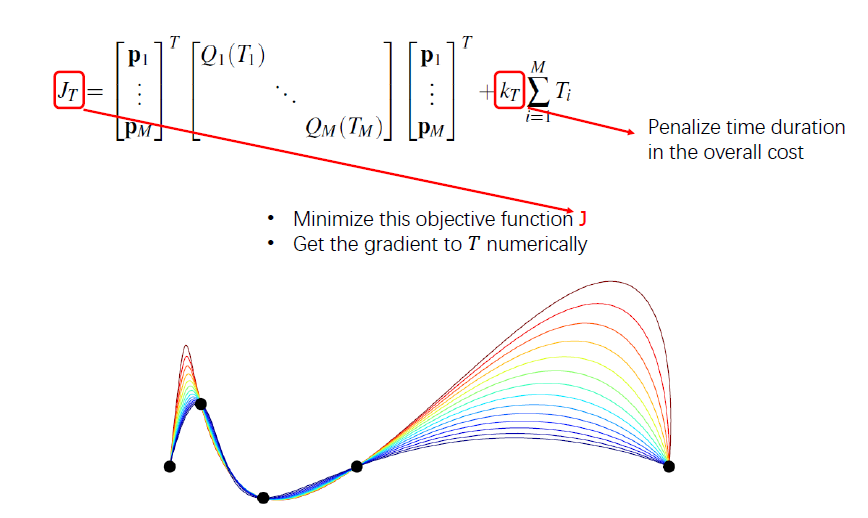
但是,如何求解呢?
由于前一部分包含\(T\),因此该函数无法对\(T\)进行求导。
使用数值求导的方法,对每个变量进行小的变化,进而计算其数值导数。
随后沿梯度进行梯度下降,得到最终值。
 f
f
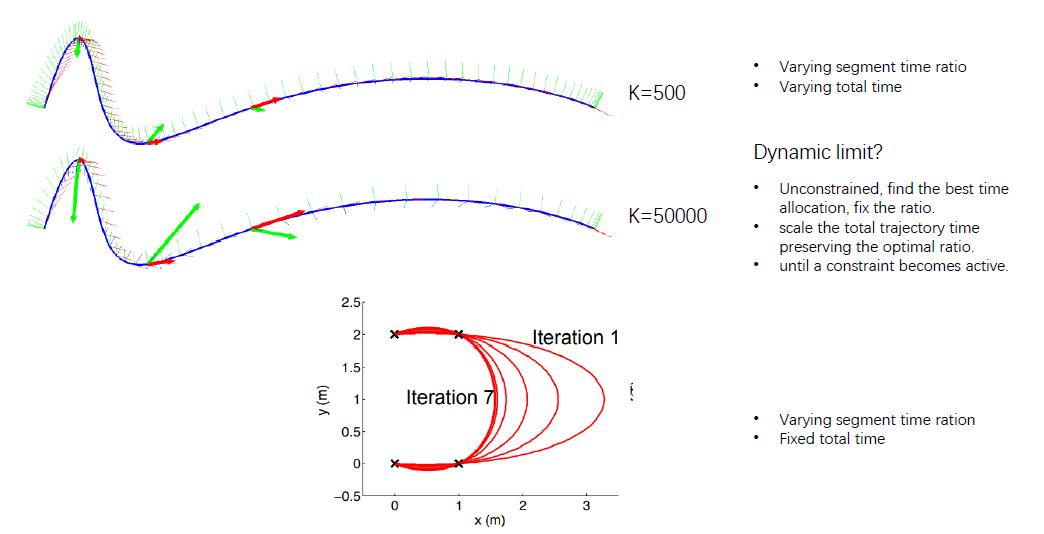
上图是总时间可调同时调整各段时间比例的情况(K是时间项在J中的权重\(K_T\))
注意:动力学此时不受约束,应先找到最佳时间分配,确定比例。
对于不满足动力学约束的段,允许时间被拉长,但各段之间保持时间的最佳比例,直到满足约束。
下图是总时间固定但调节各段时间的比例得到的结果。
Homework

本次只有等式约束,但第6章中为满足走廊限制,加入了不等式约束。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号