Motion Planning for Mobile Robots 学习笔记3

目录

• What this note covers
• Preliminaries
• Content
• Probabilistic Road Map
  • What is PRM?
  • Pros and Cons
  • Towards Improving Efficiency: Lazy collision-checking
• Rapidly-exploring Random Tree
  • Overview
  • Pros and Cons
  • Towards Improving Efficiency
    • Kd-tree
    • Bidirectional RRT/ RRT Connect
• Optimal sampling-based path planning methods
  • Rapidly-exploring Random Tree* (RRT*)
    • Recall Cons of RRT
    • RRT* Overview
    • Example
  • Kinodynamic-RRT*
  • Anytime-RRT*
• Advanced Sampling-based Methods
  • Informed RRT*
  • Cross-entropy Motion Planning
  • Other variants
• Implementation
  • Open Motion Planning Library and Moveit
  • Navigation stick - ROS
• Homework

What this note covers

第3章：基于采样的路径规划

• 第1节：概率路线图算法&快速探索随机树算法
• 第2节：基于采样的最优路径规划算法&基于采样的路径规划算法进阶
• 第3节：作业

Preliminaries

预备知识

Sampling Based-Planners

• Do not attempt to explicitly construct the C-Space and its boundaries
• Simply need to know if a single robot configuration is in collision
• Exploits simple tests for collision with full knowledge of the space
• Collision detection is a separate module-can be tailored to the application
• As collision detection improves, so do these algorithms
• Different approaches for single-query and multi-query requests

Notion of Completeness in Planning

• Complete Planner: always answers a path planning query correctly in bounded time
  完备的规划器：在一定的时间内，该规划器总能找到一条路径
• Probabilistic Complete Planner: if a solution exists, planner will eventually find it, using random sampling (e.g. Monte Carlo sampling)
  概率完备的规划器：如果存在一条路径，则一定可通过采样的方法得到该路径
• Resolution Complete Planner: same as above but based on a deterministic sampling (e.g sampling on a fixed grid).
  Resolution Complete Planner: 与上面类似，但是基于更确定性的采样（如在网格上的采样）

Content

1. Probabilistic Road Map
   环境路图的构建与如何利用环境路图寻找路径
2. Rapidly-exploring Random Tree
   快速扩展随机树，RRT
3. Optimal sampling-based path planning methods
   一些改进方法
4. Advanced path planning methods
   高等方法
5. Implementation
   应用

Probabilistic Road Map

What is PRM?

期望通过采样的方式，对地图进行简化。用少量的点代表我们的图。
在简化的图结构上寻找路径，而不是在整个地图寻找。

• A graph structure
  一种图结构
• Divide planning into two phases:
  分为两个阶段
  • Learning phase:
    学习阶段：如何简化？首先要学习图的结构
    • Sample N point in C-Space
      随机采样一部分点，最基本的方法可使用均匀采样。
    • Delete points that are not collision-free
      在障碍物中的点删除
    • Connect to nearest points and get collision-free segments.
      首先注意：起点和终点必须被连接。
      准则1.（距离准则）根据距离远近，将相距较近的点连接起来。
    • Delete segments that are not collision free.
      准则2.（障碍物准则）删除不满足碰撞检测的边。
  • Query phase:
    查询阶段：寻找路径（在空间简化图上，应用图搜索算法）
    • Search on the road map to find a path from the start to the goal (using Dijkstra's algorithm or the A* algorithm).
    • Road map is now similar with the grid map (or a simplified grid map)
• Checking sampled configurations and connections between samples for collision can be done efficiently.
• A relatively small number of milestones and local paths are sufficient to capture the connectivity of the free space

Pros and Cons

• Pros
  • Probabilistically complete
    概率完备的
  • 不用在整个环境进行搜索，相对高效
• Cons
  • Required to solve 2 point boundary value problem
    需要解决边界值问题
  • Build graph over state space but no particular focus on generating a path
    第一阶段并不关心如何生成路径，造成了一次“多余的”查询阶段
  • Not efficient
    不够有效率

Towards Improving Efficiency: Lazy collision-checking

• Lazy collision-checking
  经常性地需要检测点/边是否在障碍物内/collision-free，非常影响效率
  提出懒惰障碍物检测方法

  • Collision-checking process is time-consuming, especially in complex or high-dimensional environments.
    碰撞检查过程非常耗时，特别是在复杂或高维环境中
  • Sample points and generate segments without considering the collision (Lazy)
    不考虑是否可性的选取采样点和生成边(惰性)

  也即不考虑障碍物准则，只考虑距离准则。

  • Find a path on the road map generated without collision-checking
    在未进行碰撞检查的情况下在路线图上查找路径
  • Delete the corresponding edges and nodes if the path is not collision free.
    如果路径不是无碰撞的，删除相应的边和节点。
  • Restart path finding

虽然修改图结构会消耗一些时间，但是避免了大量的碰撞检测，节省了时间。
注意：Lazy collision-checking不仅适合于PRM，还适合于其他方法，如RRT等。

Rapidly-exploring Random Tree

快速扩展随机树（快速搜索随机树）
也是一种基于采样的路径规划算法，但与PRM相比，其更有针对性。在复杂环境/高维环境中，更有效率。

如何在空间中构造一棵树，这棵树如何帮助我们找到路径？

Overview

• Build up a tree through generating "next states" in the tree by executing random controls
  

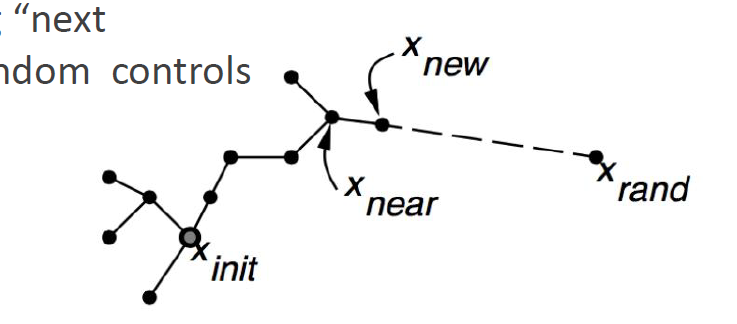
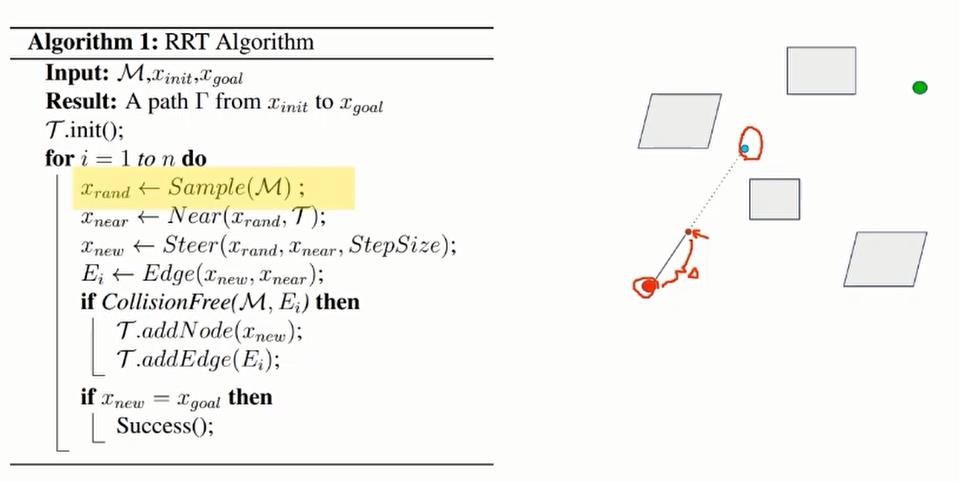
随机采样得到蓝色点，连接起点与蓝色点的线段，在这个线段上前进一段距离，得到小的红色点。
如果小红色点与连接起点和小红色点的线段都可通过碰撞检测，则将其加入树中。

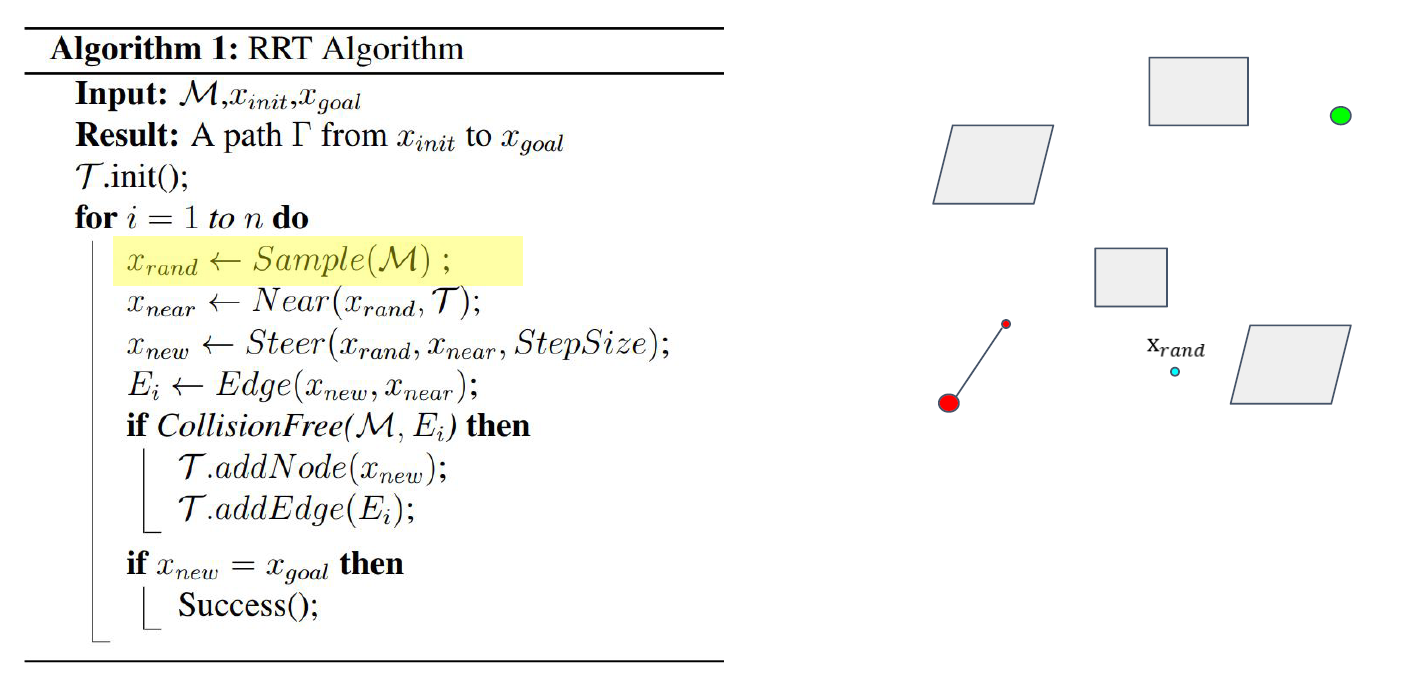
再次随机采样，得到蓝色点。
注意：这里的采样方法与PRM中类似，可以在整个空间均匀撒点，也可以用一定的采样规律撒点（偏置采样）。
在树上找到一个离蓝色点最近的一个点（从大红点和小红点中选择）<Near函数>
在二者两线上移动一定的距离，<Steer函数>
得到一个边，<Edge函数>
如果其满足碰撞检测，将其加入树中，实现一次树的扩展。<addNode函数、addEdge函数>

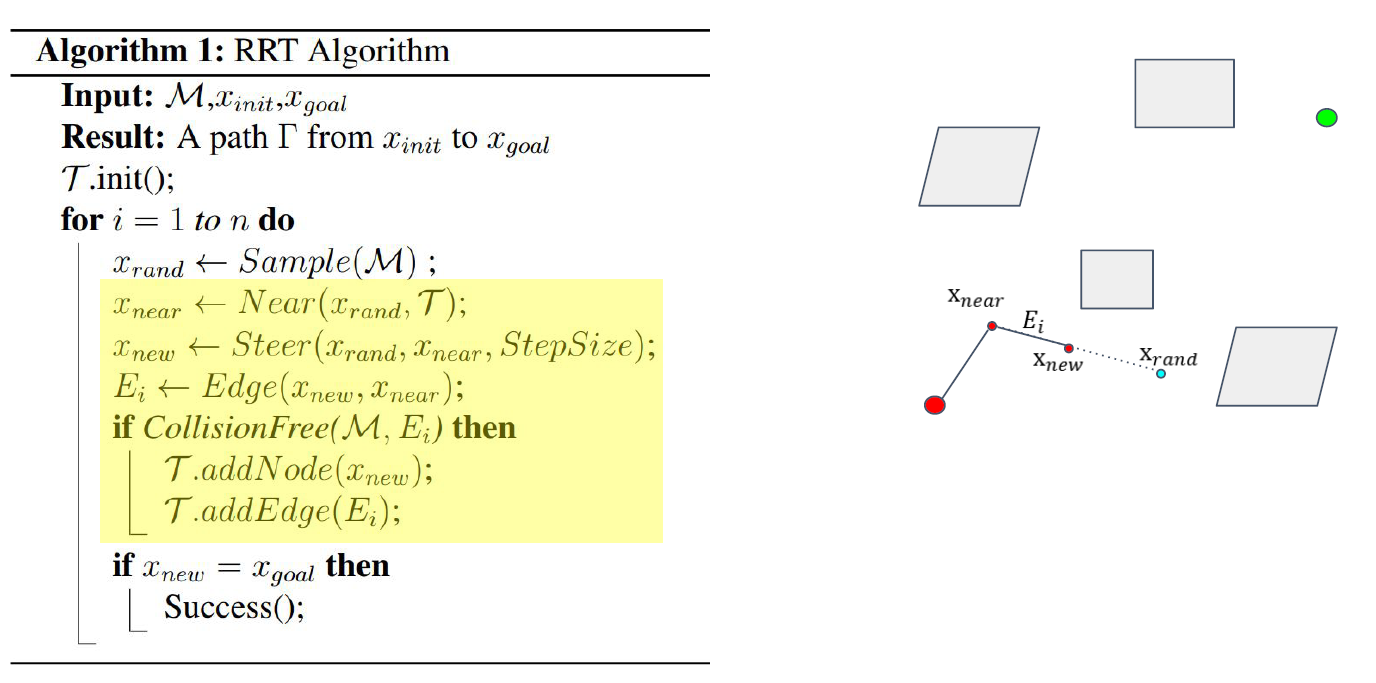
如果终点或者终点周围的点被加入树，则算法结束。
一次回溯其父节点，形成路径。

https://www.youtube.com/watch?v=pOFtvZ_qVsA

对于狭窄环境（Narrow Passage Environment），RRT的效率不高。

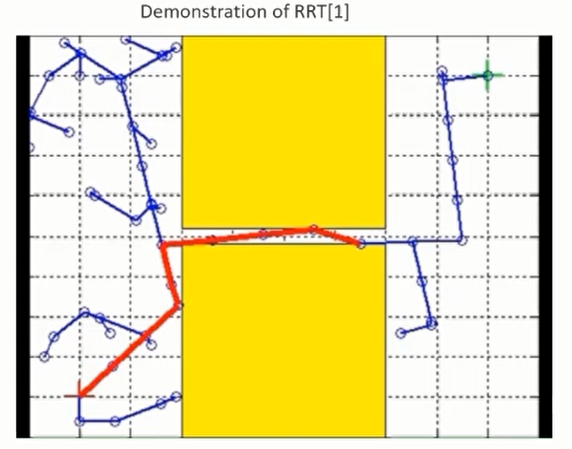
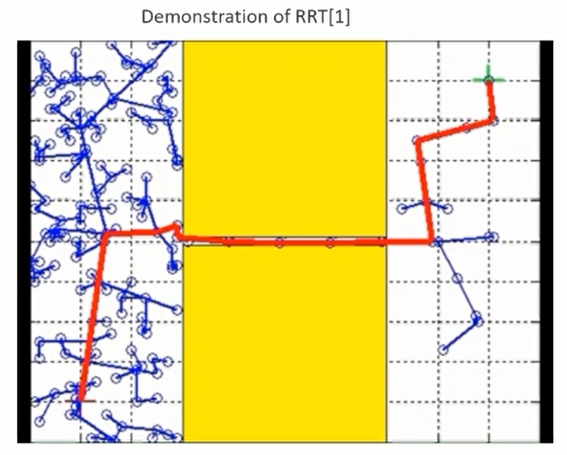
Pros and Cons

• Pros:
  • Aims to find a path from the start to the goal
    更针对目标去寻找路径
  • More target-oriented than PRM
• Cons:
  • Not optimal solution
    并不是最优解
  • Not efficient(leave room for improvement)
    并不是很高效（仍有改进的空间）
    针对伪代码中的函数进行改进
  • Sample in the whole space
    仍是在整个空间中进行采样

Towards Improving Efficiency

Kd-tree

Kd-tree：程序上的改进

改进Near函数，用于快速寻找树上最近的点。

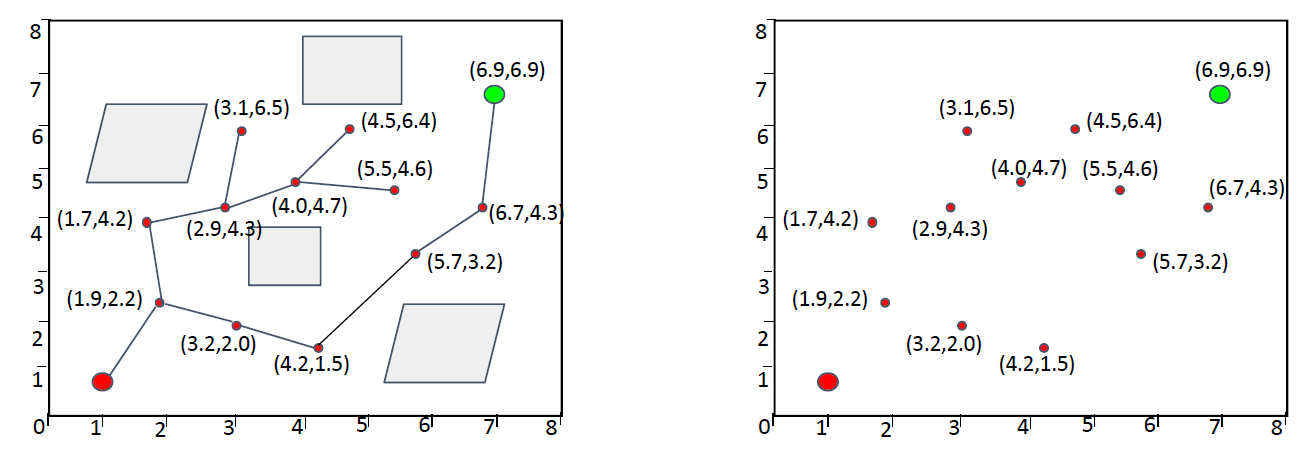
如图所示，左侧产生了一个RRT的树。
当有新的点被采样出时，如何选取最近点呢？

1. 暴力穷举
   计算所有点与该点的距离
2. Kd-tree

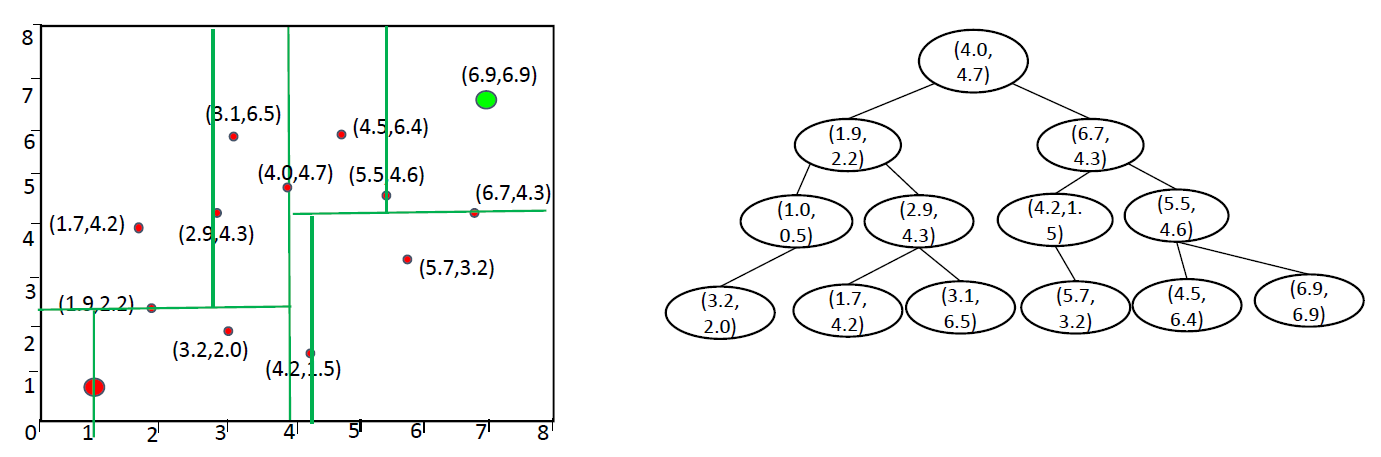
左图是Kd-tree对空间的划分。
划分方法：

1. 横向寻找所有节点坐标的中位数，将其划分为左右两支
2. 纵向寻找所有节点坐标的中位数，将其继续划分
   依次方法，持续划分

Other variants: Spatial grid, hill climbing,etc

Kd-tree的介绍：https://blog.csdn.net/junshen1314/article/details/51121582

Bidirectional RRT/ RRT Connect

• Grow a tree from both the start point and the goal point
  起点终点同时扩展两棵树，实现一次撒点，两树构建
• Path finding when two trees are connected
  当两棵树相连时，路径即产生

对于Narrow Passage的特殊情况：终点在Narrow Passage中，RRT Connect有很好的效果：

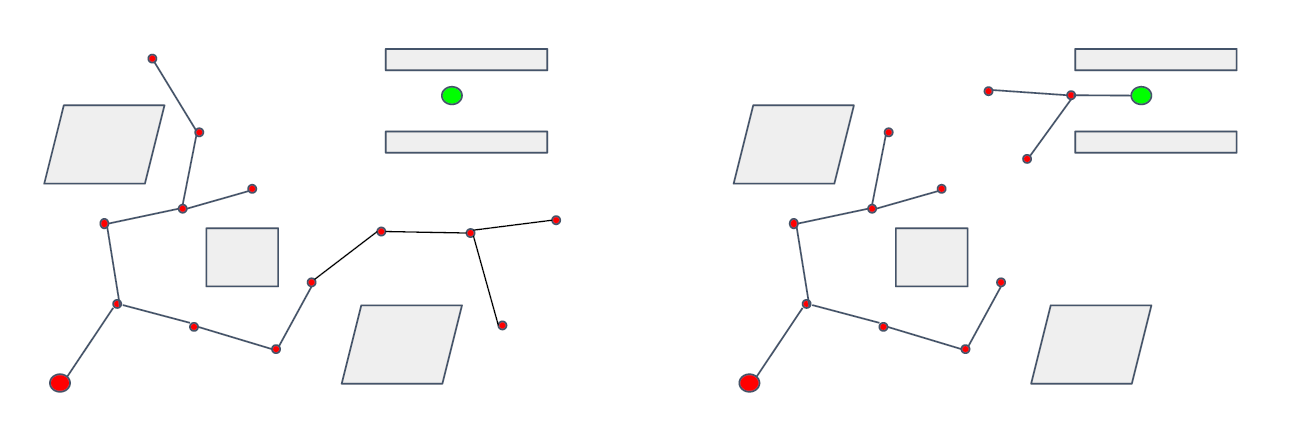
但是，对于Narrow Passage问题本身来讲，RRT Connect并不是最好的解决方式。
更多人采用改进采样的方法来解决这一问题。
设计采样函数，在Narrow Passage中多采点，从而实现树在Narrow Passage中的快速生长。

Optimal sampling-based path planning methods

基于采样的最优路径规划方法

Rapidly-exploring Random Tree* (RRT*)

Recall Cons of RRT

• Cons:
  • Not optimal solution
    并不是最优解
  • Not efficient(leave room for improvement)
    并不是很高效（仍有改进的空间）
  • Sample in the whole space
    仍是在整个空间中进行采样
  • 所产生的路径并不适合机器人执行

RRT*针对性的解决RRT生成路径不最优的问题

RRT* Overview

一开始与RRT并无区别。

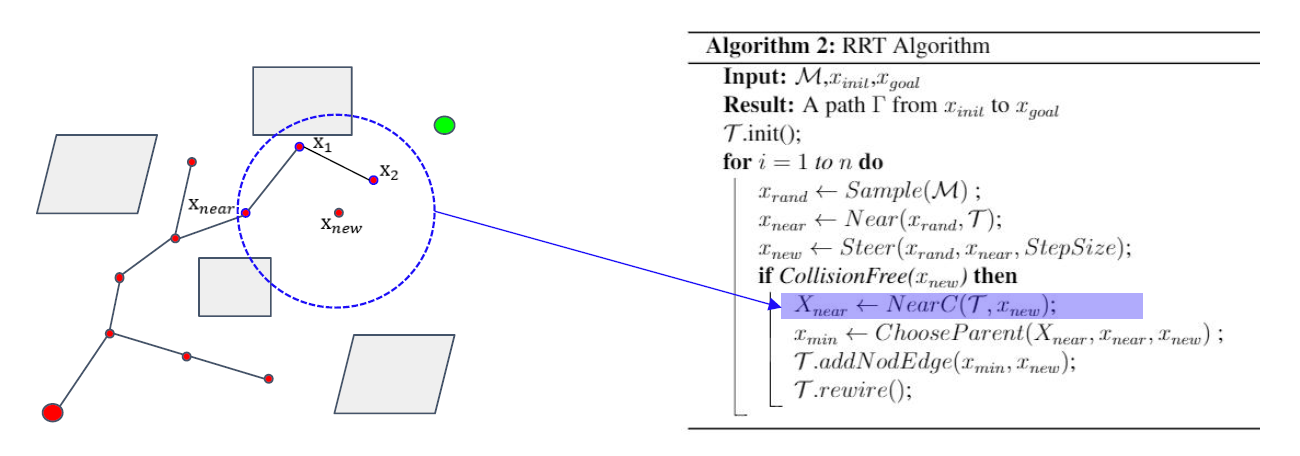
但在找到\(x_{new}\)之后，会对\(x_{new}\)周围进行搜索，寻找其附近的节点。
找到\(x_{near},x_1,x_2\)三个节点。<NearC函数>

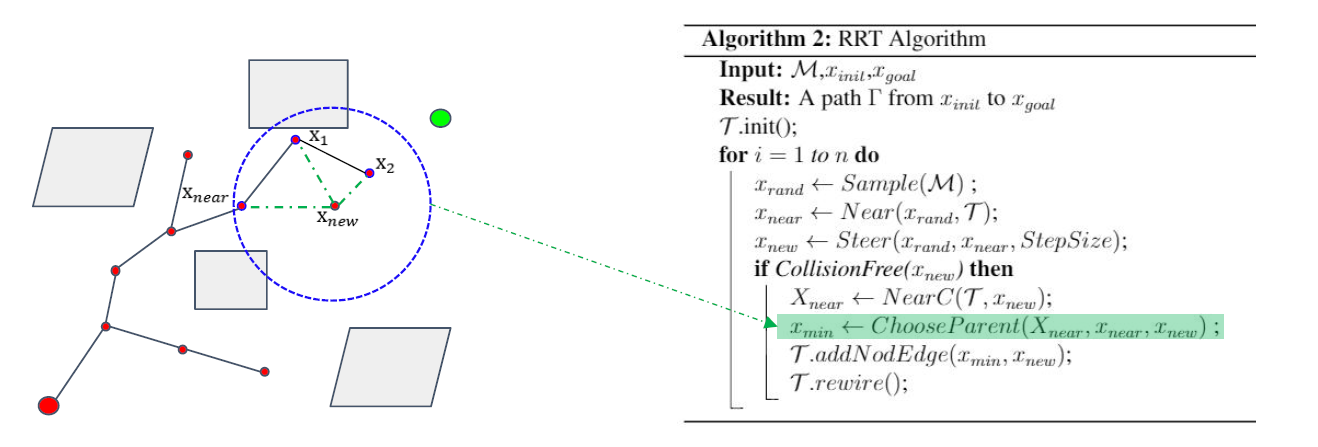
下面选取\(x_{new}\)节点的父节点。<ChooseParent函数>
分别与寻找到的三个节点连接，选取从起点经该点到\(x_{new}\)点代价（代价函数是可以自定义的）最低的点作为其父节点。

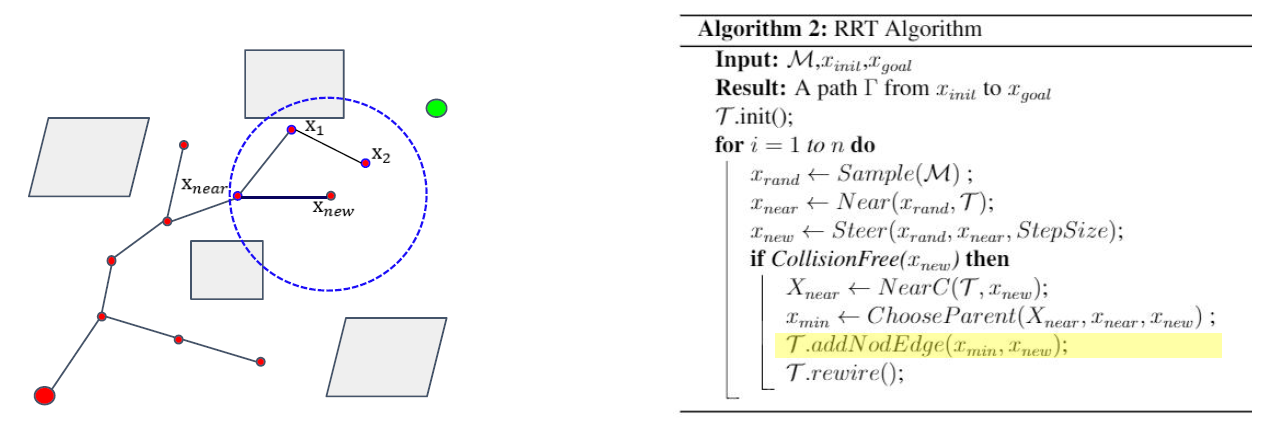
连接边与\(x_{new}\)点。<addNodEdge函数>

以上是RRT*的第一个特点（改进）
第二个特点（改进）在于对树的修改<rewire函数>

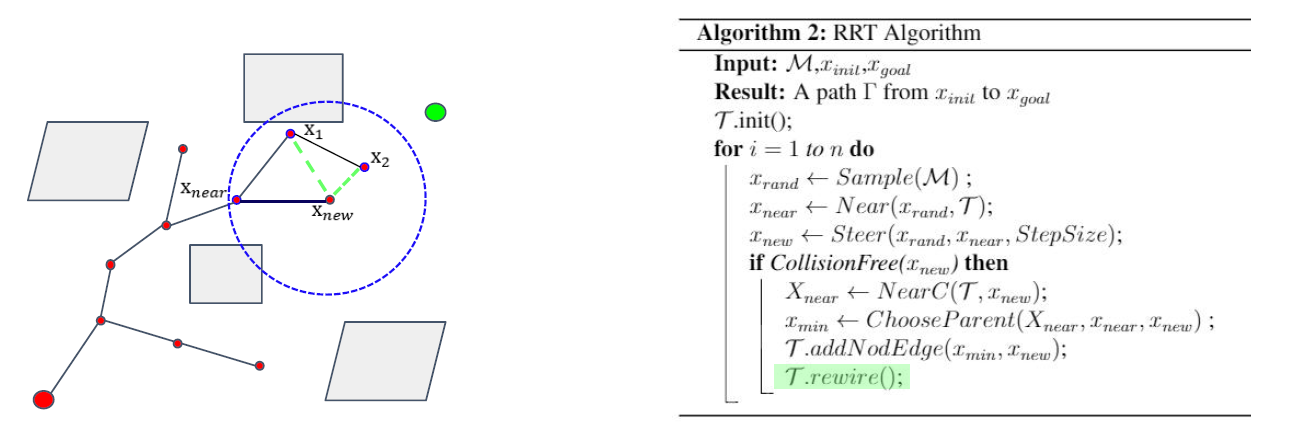
添加\(x_{new}\)之后，对于刚才未选取的备选父节点，考虑能否通过\(x_{new}\)减少从起点到达本节点的代价。
若是，则使其修改自身的父节点为\(x_{new}\)。

Example

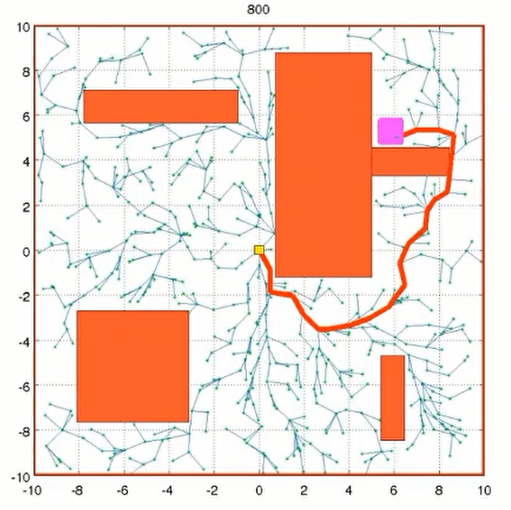
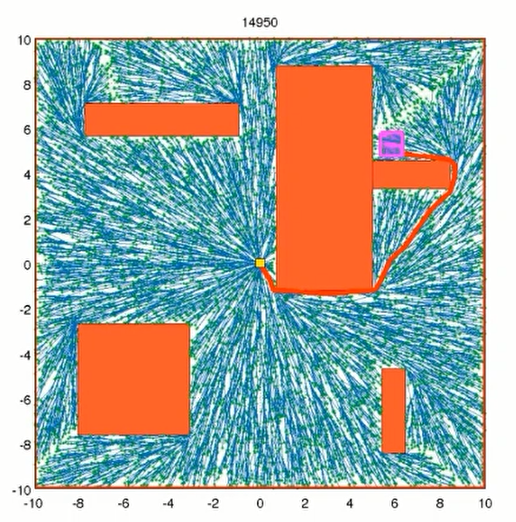
找到路径后，仍继续算法以优化路径：

https://www.youtube.com/watch?v=YKiQTJpPFkA

Kinodynamic-RRT*

不管是RRT还是RRT*，通常情况下点与点的连接都是由直线所连的，所寻找的路径也是一堆直线段组成的。
对于机器人来说，不一定可以满足其运动学约束。

Kinodynamic-RRT*用于解决这一问题，主要改进了Steer()函数。
Change Steer() function to fit with motion or other constraints in robot navigation.
考虑机器人的运动学约束或其他约束。

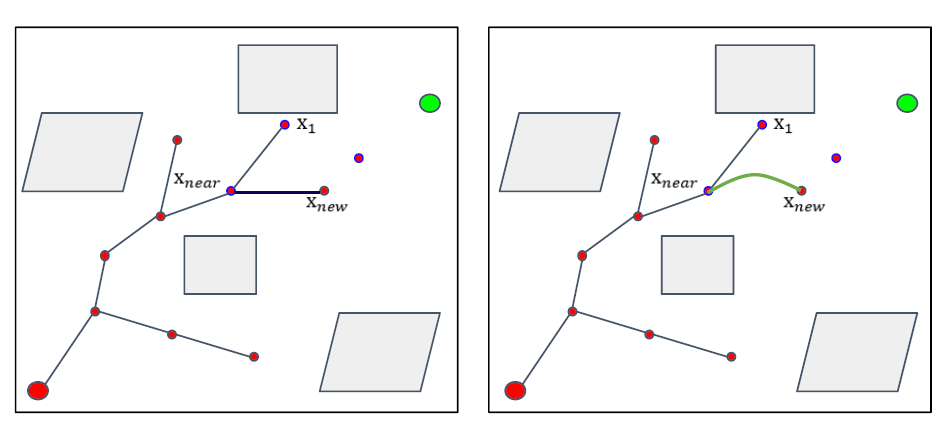
Kinodynamic RRT*: Optimal Motion Planning for Systems with Linear Differential Constraints

当采用曲线段连接各点之后，会出现一些新的问题：
比如，在左图中，连接\(x_{near}\)与\(x_{new}\)时，若使用直线段，会因为不满足碰撞检测而被舍弃。
但是，其会使用一条曲线轨迹（2），是满足碰撞检测的。

https://www.youtube.com/watch?v=RB3g_GP0-dU

此方向还是一个比较火的方向，可以多做了解。

Anytime-RRT*

Keep optimizing the leaf RRT tree when the robot executes the current trajectory Anytime Fashion
在获得一条轨迹之后，机器人一边进行轨迹跟踪，一边同时进行RRT*的路径优化，当然起始点是实时更新的。

Anytime-RRT*能更好地适应环境变化，同时其路径也可以做到较为优化。

Advanced Sampling-based Methods

基于采样的路径规划算法进阶

重点在于采样阶段

Informed RRT*

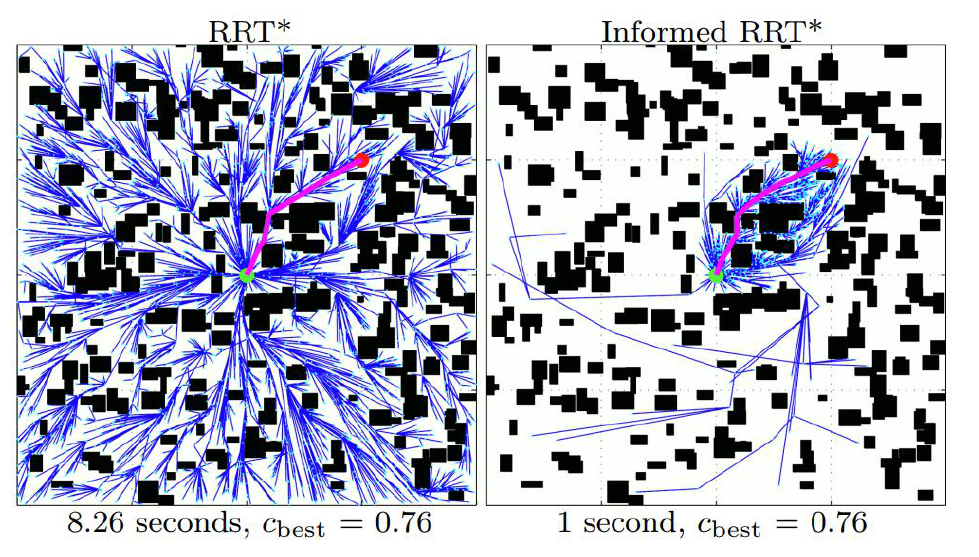
Informed RRT*: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic

当找到从起点到终点的路径之后，Informed RRT*将采样区域限定在一个椭圆中

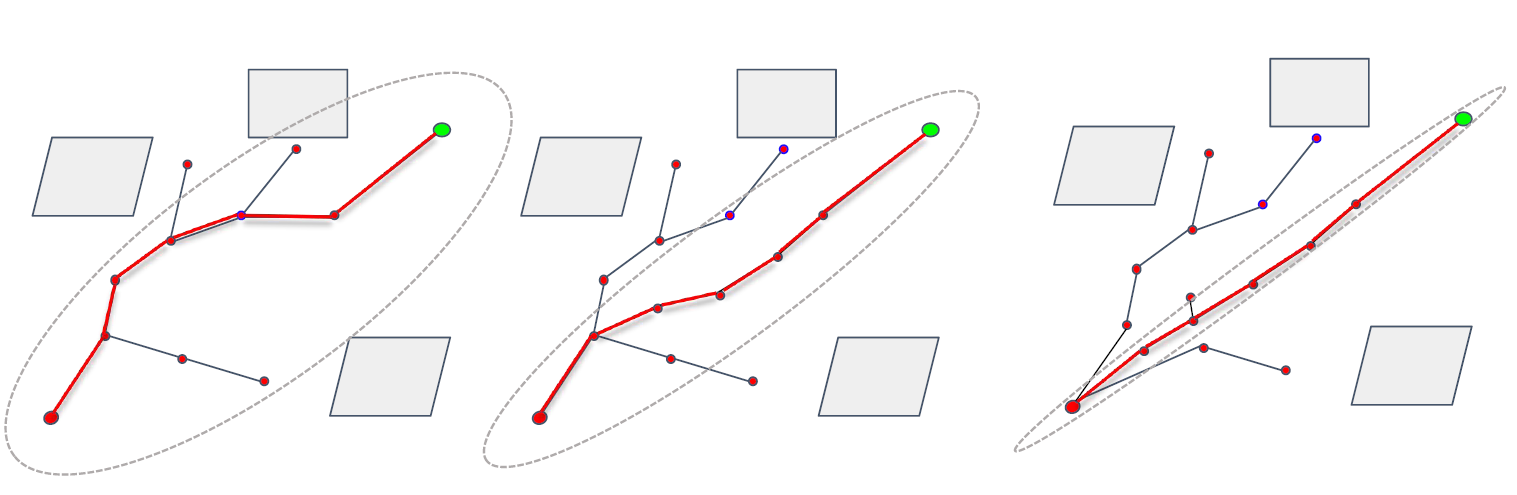
如何构建椭圆呢？
以起点和终点作为椭圆的焦点，以路径长度作为点到两个焦点的距离之和。
如果没有障碍物，椭圆会越来越扁，采样速度也会越来越快。
这里只考虑了路径最短，当然，也可以加入诸如动力学限制等。

Cross-entropy Motion Planning

也是基于RRT的方法，但是其树不是显式被构建的。

1. 生成一条路径
   可以用RRT*等各种方法。
2. 在轨迹的节点周围采样
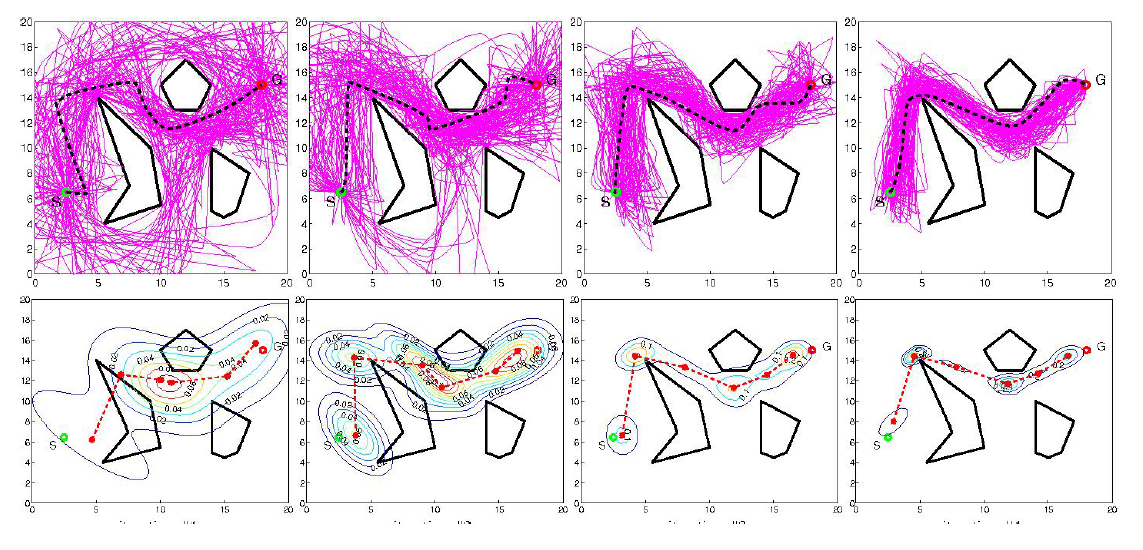
   如图，6个节点构成了一个多高斯模型，每一个部分都是以节点为均值，以所指定的方差为方差。
   在6个圈内进行采样，可以构成无数条路径。
3. 重新选取采样空间
   如图所示，得到了3条路径。现在就具有14个节点。
   对多个轨迹的多个节点求其均值，再次得到6个高斯分布。
   进行下一次的优化。

Other variants

• Lower Bound Tree RRT (LBTRRT)[a]
• parse Stable RRT[b]
• Transition-based RRT (T-RRT)[c]
• Vector Field RRTId]
• Parallel RRT (pRRT)[e]
• Etc.[f]

[1] An Overview of the Class of Rapidly-Exploring Random Trees
[2] http://msl.cs.uiuc.edu/rrt/
[a] https://arxiv.org/pdf/1308.0189.pdf
[b] http://pracsyslab.org/sst_software
[c] http://homepages.laas.fr/jcortes/Papers/jaillet_aaaiWS08.pdf
[d] https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6606360
[e] https://robotics.cs.unc.edu/publications/Ichnowski2012_IROS.pdf
[f] https://github.com/zychaoqun

Implementation

在实际中的运用

Open Motion Planning Library and Moveit

Open Motion Planning Library
集成很多路径规划的算法。
配合Moveit with ROS

[1] https://ompl.kavrakilab.org/
[2] https://moveit.ros.org/
Tutorials: [3] https://industrial-training-master.readthedocs.io/en/melodic/source/session4/Motion-Planning-CPP.html

OMPL和Moveit在机械臂中使用较多，在移动机器人中使用较少。
但移动机器人和空中机器人也可以理解成关节较少的移动机械臂。
故此方法也是可以运用的。

Navigation stick - ROS

这是专门用于移动机器人的库

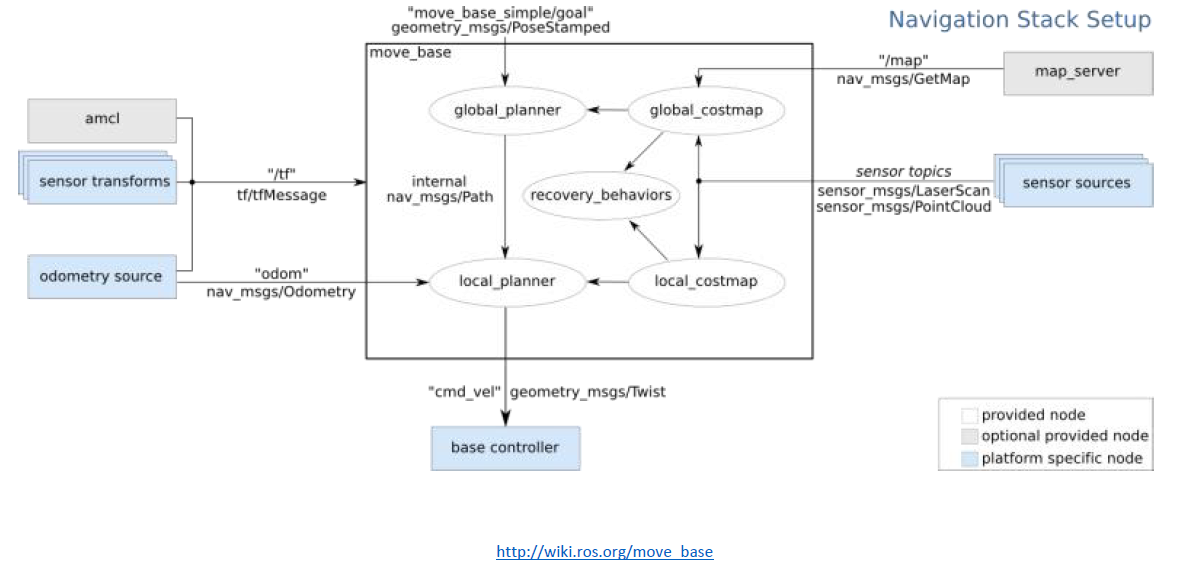
• Global planner
  不考虑太多的运动约束
  • A,D, RRTs,etc
• Local planner
  考虑具体的执行，与控制有关
  • Dwa,eband, Teb,etc

Video demonstration of RRT implemented on ROS : https://youtu.be/FsZ9b6fsQUg

Homework

• Implementation of RRT
  • You can either use MATLAB or C++
  • Hints: write RRT as a global planner in ROS
• Bonus: Implementation of Informed-RRT*