Motion Planning for Mobile Robots 学习笔记8

目录

模型预测控制是控制的一个自学科，涉及建模、优化等领域。
在此处重点关注模型预测控制在机器人学和运动规划中的运用。

Overview

  1. Introduction
  2. Linear Model Predictive Control(MPC)
  3. Non-linear MPC
  4. Homework

注意：
线性MPC往往解决凸的问题，而非线性MPC往往是一些非凸的问题。
大部分工程问题特别是运动规划中都需要使用非线性MPC。

但对于线性/非线性MPC，其核心都是解优化的过程。
但重点不在于讲解优化问题的本质和数学方法，而是多介绍求解的算子与软件工具包。

Introduction

什么是模型预测控制

  • 模型
    什么是模型？
    物理学模型：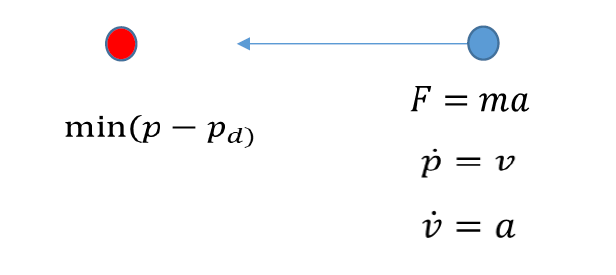
    知道一个质点的力与质量，就可以求出其位置、速度、加速度，可以完整地描述质点在未来的轨迹。

    • 系统模型
      也即其运动轨迹的描述。
      有时候系统模型可以用简单的线性方程描述。
    • 问题模型
      例如，质点需要到红色的目标点去。那么，\({\rm min}(p-p_d)\)称之为问题模型。
      但问题模型（优化目标）往往非常复杂，因此不得不用非线性的方法解决问题。

  • 预测

    • 状态空间
    • 输入空间
      给定一定的输入，其他状态（状态空间中的量）如何变化。
    • 参数空间
      由于现实世界是连续的，因此其求解十分困难。
      将力的变化放在参数空间中表达，将其变为有限阶的优化问题。

  • 控制

    • 选择最佳策略的过程

模型预测控制的一个经典描述

模型

\[\min C_{F}\left(x\left(t_{f}\right)\right)+\int_{t=t_{0}}^{t_{f}} C_{R}(x, u) d t\\ \dot{x}=f(x, u) \\ g(x, u)<0\\ h(x, u)=0\\ x \notin Obstacle \]

其代价函数由两部分组成，一是final-cost\(C_{F}\left(x\left(t_{f}\right)\right)\)，二是running-cost\(\int_{t=t_{0}}^{t_{f}} C_{R}(x, u) d t\)。

约束条件：

  • 动力学约束（系统方程）
  • 不等式条件（速度、加速度约束）
  • 等式条件（起始点、终点约束）
  • 避障条件（往往是非凸的）

参数空间

  1. 零阶保持器（直接离散化）
    给出离散频率直接离散。
  2. 多项式表示\(u(t)\)（含B-样条等）
  3. 非线性方法
  4. 数值解
  5. 机器学习的方式（如神经网络）

优化

  • 搜索：
    • 图搜索
    • 基于随机抽样的搜索
  • 凸优化：
    • 二次编程
  • 非凸优化：
    • 顺序二次编程
    • 粒子群优化(针对非凸，非线性，不连续)

控制

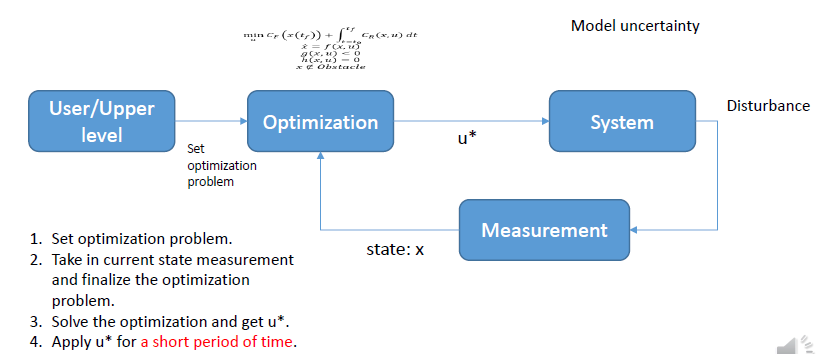
Receding Horizon Control

  1. 设置优化问题。
  2. 进行当前状态测量并最终确定优化问题。
  3. 解决优化问题并得到u *。
  4. 在短时间内应用u *。

Tube based MPC

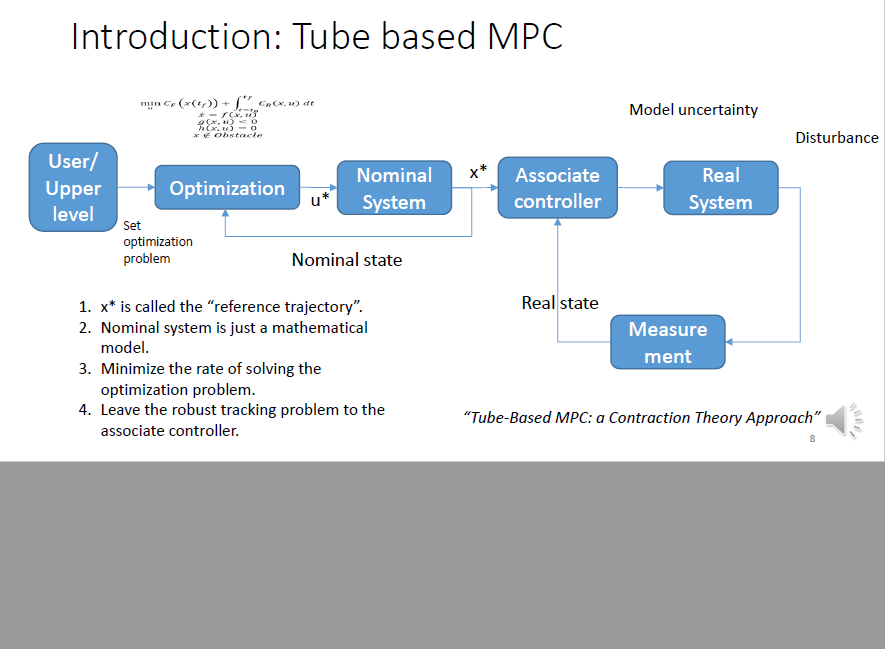
以极低的频率求解优化问题，随之以较高频率控制实际系统。
Tube：使实际系统状态在理想状态附近的一个“管道”内。

代码库

前3个可一键生成代码。

以上4个均为数值计算方法。

  • Multi-Parametric Toolbox 3
    https://www.mpt3.org/
    实现了显示MPC的方法，进行查表寻找解析解

Linear MPC

basics



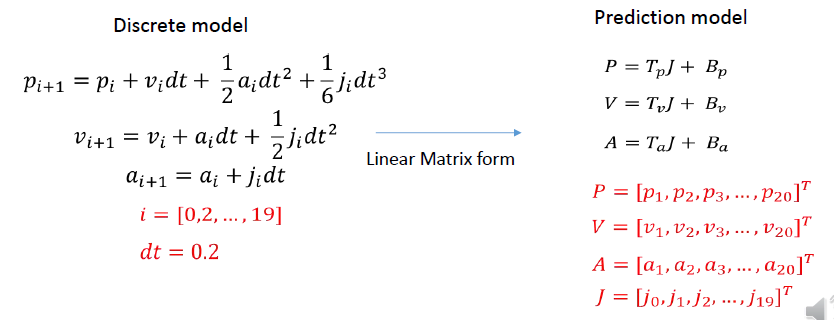
其中\(B_p\)、\(B_v\)、\(B_a\)是关于\(p_0\)、\(v_0\)、\(a_0\)的函数；
\(T_p\)、\(T_v\)、\(T_a\)是系数矩阵，\(J\)是参数空间，选定一组参数空间值后，可通过预测模型得到系统状态未来的值。

问题模型：
目标1：达到零位置，零速度和零加速度。
目标2：平滑的轨迹。

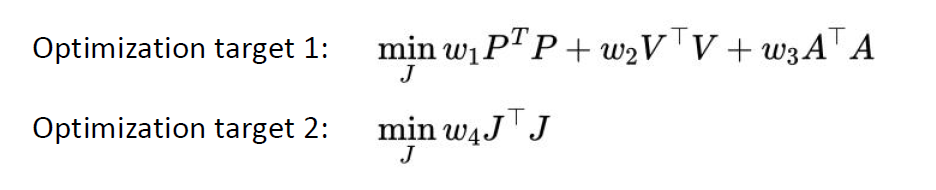
优化：

凸二次规划问题（hessian矩阵正定）

标准的4段式方法：

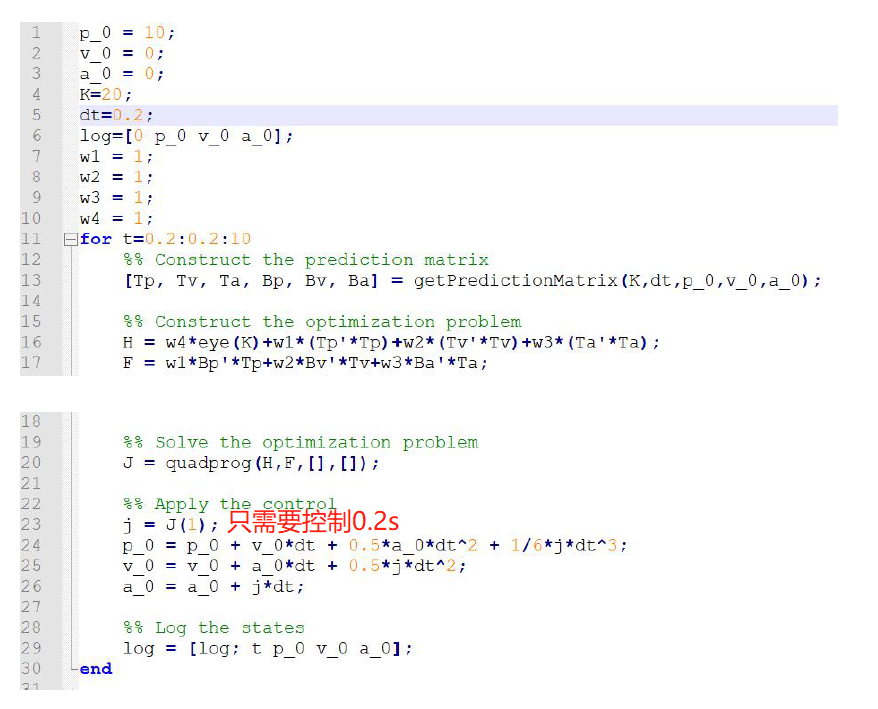
解析解：

硬约束


Less equal form是因为很多求解器仅可输入小于等于的约束条件。

模型预测控制与运动规划的不同：
由于必须在predication horizon内完成，在限制了速度与加速度之后，如果必须要求最终到达终点，很可能会没有解。
因此，大部分MPC会把终点限制放在目标函数而不是约束条件。

在MPC中也可以改变其predication horizon，但其值的增大会带来更大的计算量，过短的predication horizon会无法镇定系统（系统发散）。

软约束

如果不可避免地违反了速度和加速度约束怎么办？

如果使用硬约束：

  • 求解器不会报告任何求解！！
  • 控制器不知道该怎么办。

如何施加软约束？

加入软约束后，其不能再化为二次优化问题。
但大部分MPC算子是针对二次优化的，怎么办？

方法：

\(L\)是足够大的正数向量，以使得约束始终成立。
但不希望\(L\)过大，以免超过约束条件过多。
在目标函数中加入\(\omega_5L^TL\)。
然后所有的H，F，A，b矩阵都应进行相应调整。
\(\omega_5\)会给的很大，以使系统先将其拉回满足约束的状态，再考虑其他优化目标。

如何设置约束？

  • 状态约束->使用软约束
    它们受测量噪声和干扰的影响
  • 输入约束->使用硬约束
    它们可以任意更改，违反它们可能会损害物理系统。

线性MPC局限性：

  • 它通常需要线性模型，或者模型可以合理地线性化（自适应MPC）。
  • 本质上，障碍约束通常是非凸的。

    非凸的优化算子（如SQP）往往对初值敏感。

参数空间

多项式与零阶保持器

Boundary constrained motion primitives (BSCP)

posted @ 2020-12-06 01:19  HAN_Letisl  阅读(473)  评论(0)  编辑  收藏  举报