E. Building an Aquarium

Building an Aquarium

Building an Aquarium

题面翻译

你需要修一个水池，水池的底部高低不一，第 格高 。

如果修了一个高 的水池，会先在两侧修高度为 的墙壁防止水溢出，然后对每一格注水：

• 对于第 格，需要向其注水 个单位的水，如果 ，则不用注水。
• 水可以有剩余，但不能少，少了就无法修建高度为 的水池。

你一共有 个单位的水，问 最大能是多少。

题目描述

You love fish, that's why you have decided to build an aquarium. You have a piece of coral made of columns, the -th of which is units tall. Afterwards, you will build a tank around the coral as follows:

• Pick an integer — the height of the tank. Build walls of height on either side of the tank.
• Then, fill the tank up with water so that the height of each column is , unless the coral is taller than ; then no water should be added to this column.

For example, with 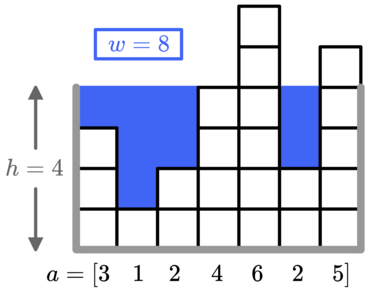and a height of , you will end up using a total of units of water, as shown. You can use at most units of water to fill up the tank, but you want to build the biggest tank possible. What is the largest value of you can select?

输入格式

The first line contains a single integer ( ) — the number of test cases.

The first line of each test case contains two positive integers and ( ; ) — the number of columns of the coral and the maximum amount of water you can use.

The second line of each test case contains space-separated integers ( ) — the heights of the coral.

The sum of over all test cases doesn't exceed .

输出格式

For each test case, output a single positive integer ( ) — the maximum height the tank can have, so you need at most units of water to fill up the tank.

We have a proof that under these constraints, such a value of always exists.

样例 #1

样例输入 #1

5
7 9
3 1 2 4 6 2 5
3 10
1 1 1
4 1
1 4 3 4
6 1984
2 6 5 9 1 8
1 1000000000
1

样例输出 #1

4
4
2
335
1000000001

提示

The first test case is pictured in the statement. With we need units of water, but if is increased to we need units of water, which is more than . So is optimal.

In the second test case, we can pick and add units to each column, using a total of units of water. It can be shown that this is optimal.

In the third test case, we can pick and use all of our water, so it is optimal.

题解

#include <bits/stdc++.h>
using namespace std;

const int N = 2e5 + 5;
int t, n, x, arr[N];

bool check(int h)
{
	long long c = 0;
	for(int i = 1; i <= n; i++)
    {
		if(arr[i] < h)
			c += h - arr[i];
    }
	return c <= x;
}

int main()
{
	
	scanf("%d", &t);
	while(t--)
    {
		scanf("%d %d", &n, &x);
		for(int i = 1; i <= n; i++)
			scanf("%d", arr + i);
		int l = 1, r = 2e9, mid, h;
		while(l <= r)
        {
			mid = (r-l)/2+l;
			if(check(mid)) 
            {
             l = mid + 1;
             h = mid;
            }
			else
            {
             r = mid - 1;
            }
		}
		printf("%d\n", h);
	}
	
	return 0;
}