第三章图的连通性

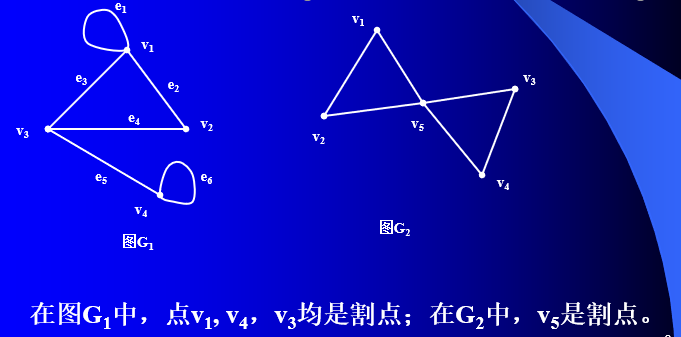
一、割边、割点和块

(一)、割边及其性质

定义1 边e为图G的一条割边，如果 \(w(G-e)>w(G)\)

定理1 边 e 是图G的割边当且仅当 e 不在G的任何圈中。

推论1 e为连通图G的一条边，如果e含于G的某圈中，则G-e连通。

(二)、割点及其性质

定义2 在G中，如果E(G)可以划分为两个非空子集E1与E2,使 G[E1]和G[E2]以点v为公共顶点，称v为G的一个割点。

定理2 G无环且非平凡，则v是G的割点，当且仅当

\[w(G-e)>w(G) \]

定理3 v 是树T的顶点，则v是割点，当且仅当v是树的分支点。

定理4 设v是无环连通图G的一个顶点，则v是G的割点，当且仅当V(G-v)可以划分为两个非空子集V1与V2,使得对任意x ∈V1, y ∈V2, 点v在每一条x y路上。

证明：

无环非平凡连通图至少有两个非割点。

恰有两个非割点的连通单图是一条路。

若v是单图G的割点，则它不是G的补图的割点。

(三)、块及其性质

定义3 没有割点的连通图称为是一个块图，简称块；G的一个子图B称为是G的一个块，如果(1), 它本身是块；(2), 若没有真包含B的G的块存在（极大性）。

定理5 若|V(G)|≧3,则G是块，当且仅当G无环且任意两顶点位于同一圈上。

(三)、块割点树

二、图的连通度与敏格尔定理

1、点连通度与边连通度的概念

定义1 给定连通图G，设 \(V^`\subseteq V(G)\) ，若G -V' 不连通，称V'为G的一个点割集，含有k个顶点的点割集称为k顶点割。G中点数最少的顶点割称为最小顶点割。

定义2 在G中，若存在顶点割，称G的最小顶点割的顶点数称为G的点连通度；否则称n-1为其点连通度。G的点连通度记为k(G), 简记为k。若G不连通，k(G)=0。

定义3 在G中，最小边割集所含边数称为G的边连通度。边连通度记为λ(G) 。若G不连通或G是平凡图，则定义λ(G) =0

定义4 在G中，若k (G)≧ k, 称G是k连通的；若λ(G)≧k，称G是k边连通的。

2、连通度的性质

定理1 (惠特尼1932) 对任意图G，有：

\[k(G)\leq \lambda (G)\leq\delta (G) \]

定理2 设G是(n, m)连通图，则：

\[k(G) \leq \lfloor \frac{2m}{n} \rfloor \]

定理3 设G是(n, m)单图，若

\[\delta (G) \geq \lfloor \frac{n}{2} \rfloor \]

则G连通。

定理4 设G是(n, m)单图，若对任意正整数k ,有：

\[\delta (G) \geq \frac{n+k-2}{2} \]

则G是k连通的。

定理5 设G是n阶单图，若\(\delta (G) \geq \lfloor \frac{n}{2} \rfloor\)，则有

\[\lambda(G)=\delta (G) \]

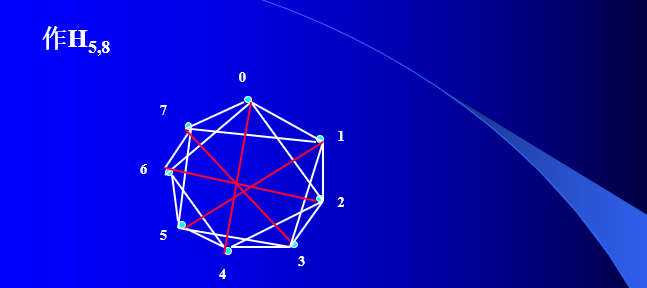
3、哈拉里图

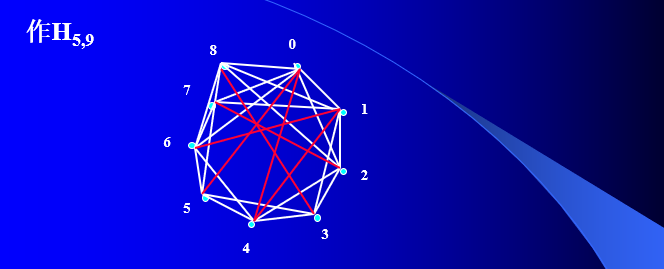
哈拉里图:涉及可靠性通信网络构建

1962年，数学家哈拉里构造了连通度是k,边数为 \(m=\lfloor \frac{nk}{2} \rfloor\)的图\(H_{k,n}\),称为哈拉里图。

(1) \(H_{2r,n}\)

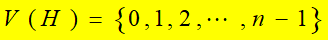
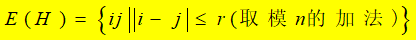
(1) \(H_{2r+1,n}\) (n为偶数)

(1) \(H_{2r+1,n}\) (n为奇数)

4、描述连通性的其它参数简介(内容拓展)

1、图的坚韧度

2、图的核度

三、图的宽直径简介

(一)、敏格尔定理

敏格尔定理是图的连通性问题的核心定理之一，它描述了图的连通度与连通图中不同点对间的不相交路的数目之间的关系。

定义1 设u与v是图G的两个不同顶点，S表示G的一个顶点子集或边子集，如果u与v不在G-S的同一分支上，称S分离u和v。

如果图中两条（x，y）路,此两条路仅x和y是其公共点。称这两条路为内部不相交的或独立的

设x与y是图G中两个不同点，称一组点（边）分离x与y是指G中删去这组点（边）后不再有（x，y）路。

定理1 (敏格尔1902---1985)

设x与y是图G中的两个不相邻点，则G中分离点x与y的最少点数等于独立的(x, y)路的最大数目；（点形式）
设x与y是图G中的两个不同顶点，则G中分离点x与y的最少边数等于G中边不重的(x, y)路的最大数目。（边形式）

定理2 (惠特尼1932) 一个非平凡的图G是k (k≧2)连通的，当且仅当G的任意两个顶点u与v间，至少存在k条内点不交的(u ,v)路。

例题：

1、设G是k连通图，S是由G中任意k个顶点构成的集合。若图H是由G通过添加一个新点w以及连接w到S中所有顶点得到的新图，求证：H是k连通的。

2、设G是k连通图，u , v1,v2,…,vk为G中k+1个不同顶点。求证：G中有k条内点不交路(u ,vi) (1≦i≦k)

定理3 (惠特尼1932) 一个非平凡的图G是k (k≧2)边连通的，当且仅当G的任意两个顶点间至少存在k条边不重的(u ,v)路。

推论对于一个阶至少为3的无环图G，下面三个命题等价。

(1) G是2连通的；

(2) G中任意两点位于同一个圈上；

(3) G无孤立点，且任意两条边在同一个圈上。

(二)、图的宽直径相关概念

(三)、一些主要研究结果简介

总结：常用符号

\(k(G)\) 表示图G的点连通度

\(\lambda(G)\) 表示图G的边连通度

总结：常用性质定理

1、敏格尔定理

设x与y是图G中的两个不相邻点，则G中分离点x与y的最少点数等于独立的(x, y)路的最大数目；（点形式）
设x与y是图G中的两个不同顶点，则G中分离点x与y的最少边数等于G中边不重的(x, y)路的最大数目。（边形式）

2、惠特尼定理

一个非平凡的图G是k (k≧2)边连通的，当且仅当G的任意两个顶点间至少存在k条边不重的(u ,v)路。