第二章树

一、树的概念与性质

定义1 不含圈的图称为无圈图，树是连通的无圈图。

定义2 称无圈图G为森林。

注: (1) 树与森林都是单图;

(2) 树与森林都是偶图。

定理1 每棵非平凡树至少有两片树叶。

定理2 图G是树当且仅当G中任意两点都被唯一的路连接。

定理3 设T是(n, m)树，则：\(m=n-1\)

推论1 具有k个分支的森林有n-k条边。

定理4 每个n阶连通图的边数至少为n-1.

定理5 任意树T的两个不邻接顶点之间添加一条边后，可以得到唯一圈。

离心率、半径、直径、中心点、中心

(1)图的顶点的离心率

(2)图的半径

(3)图的直径：最大离心率。

(4)图的中心点：离心率等于半径的点。

(5)图的中心：中心点的集合。

(6)树的形心概念与性质

设u是树T的任意一个顶点，树T在顶点u的分支是指包含u作为一个叶点的极大子树，其分支数为顶点u的度数；树T在u点的分支中边的最大数目称为点u的权；树T中权值最小的点称为它的一个形心点。全体形心点的集合称为树T的形心。

定理7 每棵树的中心由一个点或两个相邻点组成。

定理8 每一棵树有一个由一个点或两个邻接的点组成的形心。

二、生成树

(一)、生成树的概念与性质

定义1 图G的一个生成子图T如果是树，称它为G的一棵生成树；若T为森林，称它为G的一个生成森林。

生成树的边称为树枝，G中非生成树的边称为弦。

定理1 每个连通图至少包含一棵生成树。

推论若G是(n, m)连通图，则m≧n-1

注：连通图G的生成树一般不唯一

(二)、生成树的计数

1、凯莱递推计数法

定义2 图G的边e称为被收缩，是指删掉e后，把e的两个端点重合，如此得到的图记为G.e

定理2 (Cayley) 设e是G的一条边，则有：

\[\tau(G) = \tau(G-e)+\tau(G.e) \]

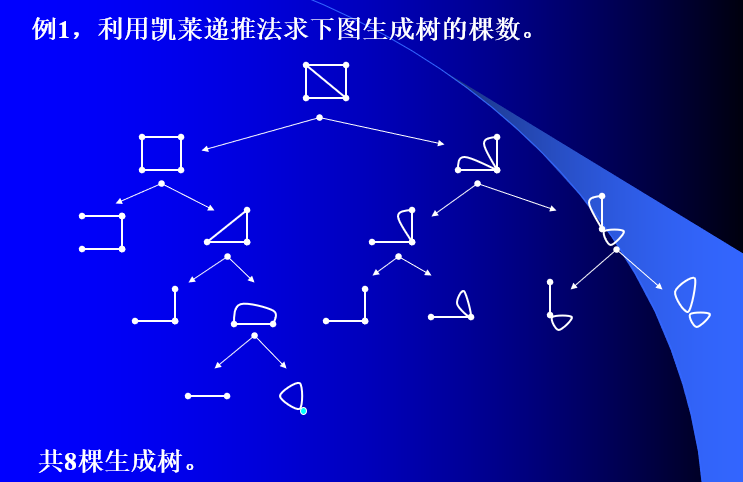
凯莱公式的缺点之一是计算量很大，其次是不能具体指出每棵生成树。

2、关联矩阵计数法

定义3 ：n×m矩阵的一个阶数为min｛n, m｝的子方阵，称为它的一个主子阵；主子阵的行列式称为主子行列式。

定理3 设\(A_m\)是连通图G的基本关联矩阵的主子阵，则\(A_m\)奇异的充分必要条件是相应于\(A_m\)的列的那些边构成G的一棵生成树。

注：基本关联矩阵为关联矩阵中划去任意结点V所对应的行。

该定理给出了求连通图G的所有生成树的方法：

(1) 写出G的关联矩阵，进一步写出基本关联矩阵，记住参考点；

(2) 找出基本关联矩阵的非奇异主子阵，对每个这样的主子阵，画出相应的生成树。

该方法的优点是不仅指出生成树棵数，而且能绘出所有不同生成树；缺点是找所有非奇异主子阵计算量太大！

3*、矩阵树定理

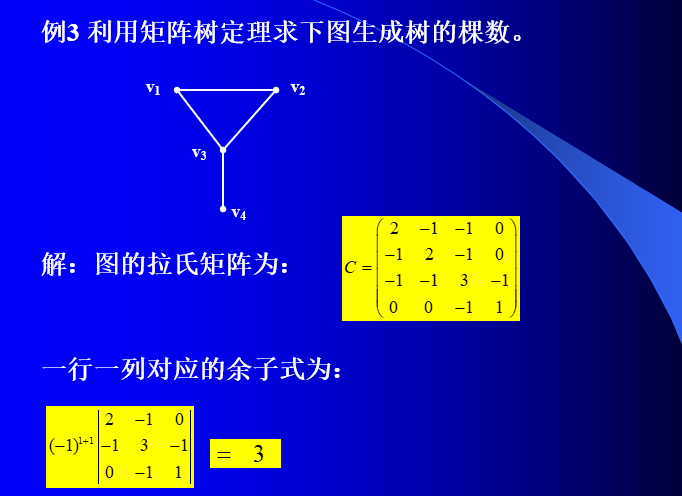
定理4 (矩阵树定理) 设G是顶点集合为V(G)=｛v1,v2,…,vn｝,的图，设A=(aij)是G的邻接矩阵，C=(cij)是n阶方阵，其中：

\[c_{ij}= \left \{ \begin{aligned} d(v_i),i\neq j \\ -a_{ij}, i\neq j \end{aligned} \matrix{} \right . \]

则G的生成树棵数为C的任意一个余子式的值。

定理中的矩阵C又称为图的拉普拉斯矩阵，又可定义为：

\[C = D(G)-A(G) \]

其中，D(G)是图的度对角矩阵，即主对角元为对应顶点度数，其余元素为0。A(G)是图的邻接矩阵。

定理7 \(\tau(K_n)=n^{n-2}\)

(二)、回路系统简介

定义4 设T是连通图G的一棵生成树，把属于G但不属于T的边称为G关于T的连枝，T中的边称为G关于T的树枝。

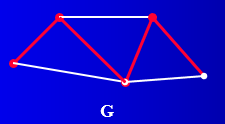
在上图中，红色边导出图的一棵生成树。则红色边为G对应于该生成树的树枝，白色边为G对应于该生成树的连枝

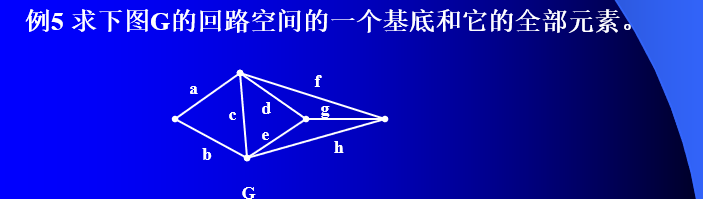
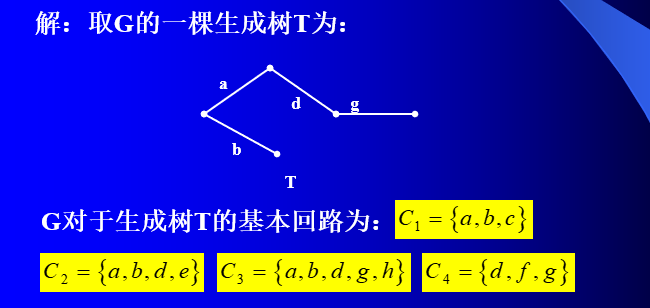
定义5 设T是连通图G的一棵生成树，由G的对应于T一条连枝与T中树枝构成的唯一圈C，称为G关于T的一个基本圈或基本回路。若G是(n, m)连通图，把G对应于T的m-n+1个基本回路称为G对应于T的基本回路组。记为\(C_f\) .

定理4 设T是连通图G=(n, m) 的一棵生成树,C1, C2,…,Cm-n+1是G对应于T的基本回路组。定义：1.Gi=Gi , 0.Gi=Φ,Gi是G的回路。则G的回路组作成的集合对于该乘法和图的对称差运算来说作成数域F=｛0,1｝上的m-n+1维向量空间。

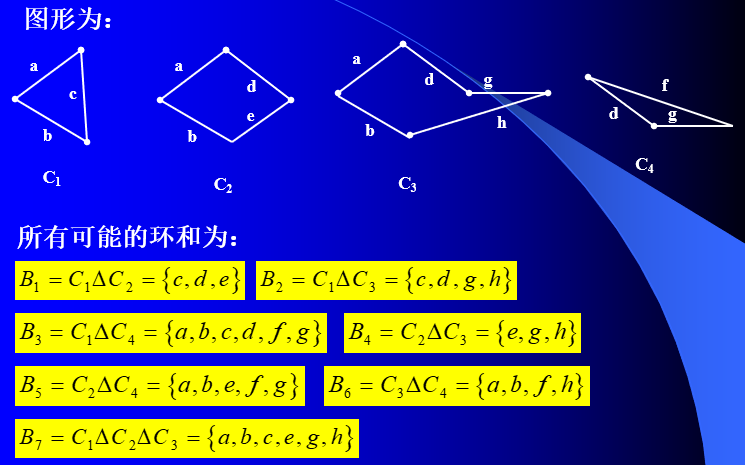
说明: 连通图G的所有回路作成子图空间的一个子空间，该空间称为回路空间或回路系统。

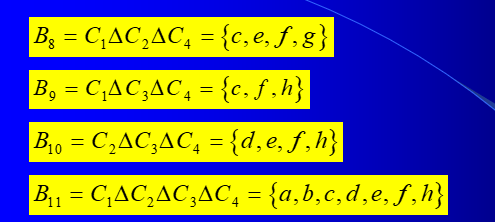
三、最小生成树

在图中求所谓的最小生成树问题。或称为赋权图中的最小连接问题。

最小连接问题的一般提法为：

在连通边赋权图G中求一棵总权值最小的生成树。该生成树称为最小生成树或最小代价树。

(一)、克鲁斯克尔算法

1、算法思想 从G中的最小边开始，进行最小权避圈式扩张。

定理1 由克鲁斯克尔算法得到的任何生成树一定是最小生成树。(证明略)

(二)、管梅谷的破圈法

破圈法求最小生成树的求解过程是：从赋权图G的任意圈开始，去掉该圈中权值最大的一条边，称为破圈。不断破圈，直到G中没有圈为止，最后剩下的G的子图为G的最小生成树。

(三)、Prim算法

对于连通赋权图G的任意一个顶点u，选择与点u关联的且权值最小的边作为最小生成树的第一条边e1;

在接下来的边e2,e3,…,en-1 ,在与一条已经选取的边只有一个公共端点的的所有边中，选取权值最小的边。

(四)、根树简介

1.概念

定义2：一棵树T，如果每条边都有一个方向，称这种树为有向树。对于T的顶点v来说，以点v为终点的边数称为点v的入度，以点v为起点的边数称为点v的出度。入度与出度之和称为点v的度。

定义3：一棵非平凡的有向树T，如果恰有一个顶点的入度为0，而其余所有顶点的入度为1，这样的的有向树称为根树。其中入度为0的点称为树根，出度为0的点称为树叶，入度为1，出度大于1的点称为内点。又将内点和树根统称为分支点。

定义4：对于根树T，顶点v到树根的距离称为点v的层数；所有顶点中的层数的最大者称为根树T的树高。

定义5：对于根树T，若规定了每层顶点的访问次序，这样的根树称为有序树(先序遍历，中序遍历，后序遍历)。

定义6：对于根树T，由点v及其v的后代导出的子图，称为根树的子根树。

定义7：对于根树T，若每个分支点至多m个儿子，称该根树为m元根树；若每个分支点恰有m个儿子，称它为完全m元树。

2.性质

定理2 在完全m元树T中，若树叶数为t , 分支点数为i , 则：

\[(m-1)i =t-1 \]

3.有序树转为二元树

4.最优二元树

定义8 设T是一棵二元树，若对所有t片树叶赋权值wi(1≦i≦t),且权值为wi的树叶层数为L(wi),称：

\[W(T)=\sum_{i-1}^t w_i L(w_i) \]

为该赋权二元树的权。而在所有赋权为wi的二元树中W(T)最小的二元树称为最优二元树。

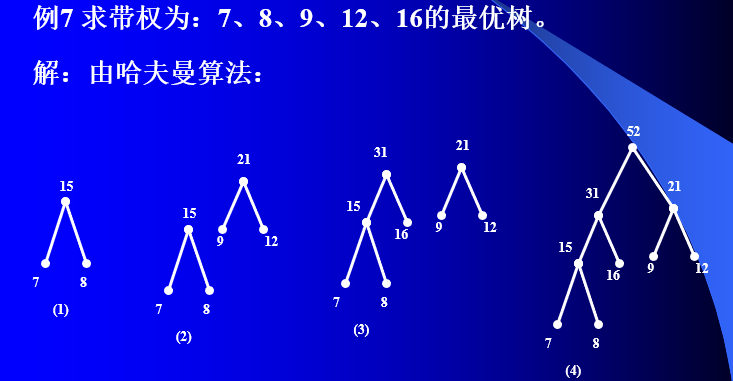
哈夫曼算法：

总结：常用符号说明

T 树

\(\tau(G)\) 表示G的生成树棵数。

\(A(G)\) 表示图G的邻接矩阵

\(D(G)\) 表示图G的度对角矩阵

总结：常用性质定理

1、最小生成树求法：

1.克鲁斯克尔算法（避圈法）

2.管梅谷的破圈法

3Prim算法

2、矩阵树定理：求图G的生成树的棵数

则G的生成树棵数为C的任意一个余子式的值。定理中的矩阵C又称为图的拉普拉斯矩阵，又可定义为：