[文章翻译]时间序列异常检测
文章目录
背景介绍
项目上需要一个工具用来监控实时数据系统插入到mongodb是否异常,主要是为了及时发现一旦数据数据系统异常(不送、少送数据),能及时的给相关人员发现警报,减少数据的损失。 比较简单的思路是通过设置阈值模型来过预警,一旦一定时间内送过来的实时数据数量少于一定值时,则发出警报。但是我们希望能有一个更智能的系统,于是考虑利用机器学习中的时间序列分析算法来做异常检测,因为数据的产生也有忙时闲时,不能一棍子打死。
生产环境能拿到的数据有限,只有每分钟Event的count值和unix时间戳。
以下是研究时间序列异常检测中找到的一篇论文,和我们的需求很相似,于是简单做了以下翻译,希望能得到启发。
Time Series Anomaly Detection; Detection of anomalous drops with limited features and sparse examples in noisy highly periodic data | Dominique T. Shipmon, et al. | [arXiv’ 17] | pdf
文章翻译
Abstract 摘要
Google通过分析来自行业合作伙伴的连续数据流,以便向用户提供准确的结果。流量意外下降可能预示着某些潜在问题的发生,是采取补救措施的预警。检测这样的下降是非常重要的,因为流是可变的并且有噪声的,在流量数据中具有大致规则的尖峰(在许多不同的形状中)。我们研究了我们是否可以预测这些数据流中的异常的问题。我们的目标是利用机器学习和统计方法对周期性但嘈杂的流量模式中的异常下降进行分类。由于我们没有大量的标记示例直接应用监督学习进行异常分类,我们分两部分来解决这个问题。首先,我们使用TensorFlow训练我们的各种模型,包括DNN,RNN和LSTM,使用回归模型并预测时间序列中的预期值。其次,我们创建了异常检测规则,将实际值与预测值进行比较。由于问题需要找到持续的异常,而不仅仅是数据中的短暂延迟或瞬间不活动,我们的两种检测方法侧重于连续的活动部分,而不仅仅是单个点。我们尝试了我们的模型和规则的多种组合,发现使用我们的两种异常检测方法的交集被证明是检测几乎所有模型中的异常的有效方法。在此过程中,我们还发现并非所有数据都属于我们的实验假设,因为一个数据流没有周期性,因此没有基于时间的模型可以预测它。
Keywords 关键词
异常;离群; 异常检测; 异常值检测; 深度神经网络; 递归神经网络; 长短期记忆网络
INTRODUCTION 简介
-
关于数据
我们查看了以5分钟为间隔保存的14组不同数据。 这意味着每小时有12个数据点,每天有288个数据点。我们的目标是检测异常情况,例如在吞吐量意外减少时缺少每日流量突发,而不检测常规低点的(甚至0)异常值。 此数据集的唯一两个属性是unix时间戳和每秒字节数值,每5分钟采样一次。 虽然这些数据中没有准确的异常标记,但并不意味着它们不存在,只是我们在本项目开始时没有任何信息。 -
关于问题
当存在异常数据的明确标签时,可以构建二元分类器来预测异常和非异常点。 对于这些问题,存在大量可供选择的技术,包括聚类分析,隔离森林和使用人工神经网络构建的分类器。 这些都在异常检测领域显示出前景[1]。 这两种技术中的前两种不仅需要用于训练的标签,而且在有许多功能时也是最有效的。 由于这些原因,它们对时间序列数据不那么有用,特别是当我们没有其他功能可访问时。神经网络可以有效地预测周期时间序列数据,如傅里叶级数等更简单的技术。 但是,因为被视为异常的东西可能因数据而异,所以每个问题都可能需要自己的模型。 有些问题有许多功能可以使用或者永远不会给出误报,而其他问题(如我们的)只有很少的功能并且需要连续而不是点异常。
我们为每个数据流训练了一个单独的模型,因为我们发现每个数据流之间没有显着的相关性。 我们的模型使用我们的异常检测规则返回我们与实际数据流值进行比较的预测,以确定当前点是否异常。 虽然我们的所有模型和指标都是在离线环境中完成的,但它们都适用于在线培训,预测和异常检测。 我们的模型的适应性是我们的机器学习模型和异常检测规则的结果,只需要过去或当前点。 此外,为了确保我们的模型有效,我们将它们与阈值模型进行比较,阈值模型将不断预测非常低的值。由于我们的模型只是通过回归预测一个点,我们需要一个定义的规则来通过比较预测值和实际值来确定一个点是否异常。用于比较预测实际值以确定点是否异常的直观方法是简单地计算欧氏距离并设置阈值。然而,这可能导致许多误报,特别是对于噪声数据。因此,我们为异常检测实施了两种不同的检测规则:一种使用累加器检测连续中断,另一种使用艾哈迈德和普尔迪[2]概述的概率方法。两种方法都试图通过避免应用于一个数据点的简单阈值技术来降低高误报率。累加器方法的工作原理是定义一个度量来确定本地中断,然后为每次中断递增计数器,并为每个非异常值递减计数器。基于Numenta公式[2]的统计方法通过比较短期方差和长期方差来工作,这意味着它除了我们的模型之外还会调整数据[2]。我们发现这两种方法同样运作良好;他们两人几乎完全相同。尽管如此,每个方法都提供了理论和实践方法,特别是在潜在的未来实验中,因为累加器方法易于修改和控制,统计方法给出了异常值的百分比,可以在模型之间相乘以提供更强大的得分[2]。
我们发现,对于这个问题,异常检测方法比模型本身更重要,因为我们的异常规则能够在我们的大多数模型上非常有效。
RELATED WORK 相关工作
异常检测正在积极和深入研究[3] [4]。虽然分类技术是解决异常检测的常用方法,但期望始终拥有一组具有足够且多样化的标记异常的数据集是不现实的[1]。在这些情况下,统计和回归技术似乎更有希望。 Netflix最近发布了使用鲁棒主成分分析[5]在大数据中进行异常检测的解决方案。 Netflix的解决方案被证明是成功的,然而,他们的统计方法依赖于高基数数据集来计算低秩近似,这限制了它的应用[5]。 Twitter还发布了一种异常检测方法,该方法使用季节性混合极端学生化偏差测试(S-H-ESD)来考虑季节性[6]。 Twitter采用的技术是有前途的,因为它适用于突破性异常,而不仅仅是点异常[6]。还有许多其他机器学习技术可用于检测异常,例如使用LSTM,RNN,DNN或其他模型类型进行回归[1]。在本文中,我们关注基于回归的机器学习技术在周期性时间序列数据上的性能,这些数据具有有限的特征和很少的异常标记示例。
DATA PREPROCESSING AND INITIAL ANALYTICS 数据预处理与初始分析
我们可以使用的唯一功能是unix时间戳,唯一的标签是接收的字节数(数据量)。 因此,我们想要弄清楚我们可以使用哪些方法来创建与原始时间戳功能不线性相关的其他功能。 虽然傅立叶级数只能处理单个值,但其他机器学习方法可以更好地处理更多功能。 此外,由于我们正在对标签进行培训,因此它不能作为输入功能,这意味着没有任何特征工程,我们的模型只能使用一个特征。
我们决定查看任何形式的复合数据流是否有意义作为特征,例如所有流的平均值或使用主要组件将其减少到几个重要流。 然而,我们发现通过计算协方差矩阵,几乎没有任何流具有任何线性相关性,这意味着基于主成分分析的复合物不会有附加信息。
因此,我们的所有功能都必须来自我们正在使用的单个数据流。对于我们的每个网络模型,我们将unix时间戳转换为工作日,小时和分钟功能。然后我们通过将小时和工作日转换为一个热编码,将时间特征分解为多个非线性相关特征,同时添加线性分钟特征,希望通过创建具有更复杂关系的更多特征来帮助模型更好地学习。我们还决定尝试使用过去标签的衍生物作为特征。在不使用导数的情况下,唯一可能的变化是在模型中输入的最大时间范围内,在我们的例子中是一周。这意味着我们的模型每周都会预测相同的值。此外,使用过去数据点的衍生物的选择是由其在在线监测中使用的能力所驱动的。虽然使用我们试图预测的值计算的特征通常是由于过度拟合而导致的不良实践,但我们希望导数与弱相关性足够 - 特别是作为标签的非线性变换 - 模型将时间学习为一个更重要的特征。当我们将异常模拟为连续值(例如0)时,我们发现它继续预测尖峰,虽然它们略小,表明我们的模型并没有过度拟合导数
我们将每秒字节数的度量标准化为从0到1,因为虽然傅里叶模型可以使用与输入值一样高且可变的值,但是当值很高时,使用神经网络的方法效果要差得多。 此外,设置这些边界允许我们使用激活函数将数据转换为-1到1或0到1,如双曲正切函数(tanh)和sigmoid函数,以尝试更多方法来优化我们的模型。 另外,对数据进行标准化使得即使对于傅里叶模型也能更快地进行训练,因此我们对所有模型使用了标准化数据。
DETECTION RULES 检测规则
我们尝试了两种类型的检测规则,累加器方法和高斯尾概率方法。 通过我们的实验,我们发现每个数据流的异常检测规则都更有效。 因此,我们发现混合模型只是两个模型的交集,在识别异常点时更有效。 我们发现每个检测规则比另一个更好的实例,因此我们使用了累加器和高斯尾概率规则的交集。
-
Accumulator 累加器
累加器规则的目标是要求在发出持续异常信号之前的短时间内发生多点异常。 我们尝试了两种不同的规则来检测点异常,然后将它们作为累加器规则的一部分进行测试。 该规则涉及一个计数器,该计数器将在检测到点异常时增长,并在预测值正确的情况下收缩。 这样做的目的是通过在短时间内要求多个异常使其达到信令阈值来防止局部异常检测算法引起的噪声。 对于每个局部异常,累加器增加1,并且对于每个非异常值,它会缩小2,这样纯噪声会导致累加器收缩。 累加器的上限为信令阈值的0到1.5倍,尽管这些数字是根据测试选择的,其他最佳值也是可能的1) Threshold 阈值
该算法将局部异常定义为当实际值大于低于预期值的给定增量时的任何值,此时实际值大于硬编码阈值,该阈值表示高于它的任何值都不是异常的。 这只是一个简单的算法,本质上也是参数化的,我们选择的值适用于我们的数据集,但对于每个可能的算法都可能不是最佳的。2)Variance Based 基于方差的
我们尝试使用局部方差来确定中断点,通过将中断定义为超出当前预测的滚动方差的20倍的任何值,使得噪声区域将允许异常中的更多噪声。然而,证明该方法的效率略低于简单阈值。因为我们发现阈值方法对我们的数据更有效,所以我们在本文的所有异常检测中都使用了这种方法。我们观察到,由于模型推断中的偏移与地面实况相比,累加器规则经常在峰值之后识别出误报。这种抵消可能是由于前几个月的培训,周期性变化可能会逐渐发生在下一个评估月份。为了减少这些误报,我们添加了一个“峰值”参数,该参数会在峰值之后将累加器减少三个,并允许累加器低于0(低至阈值)。但是,我们只希望这会在峰值之后立即影响预测,因此如果找到更多的非异常数据点,累加器将衰减回0,从而有效地阻止它在峰值之后立即预测异常。
对于我们所有的模型,我们将非异常值的阈值定义为0.3,峰值为0.35,累加器阈值为15,局部中断的增量为0.1。
-
Gaussian Tail Probability 高斯尾概率
我们决定测试数据的第二个异常检测规则是Numenta定义的高斯尾概率规则。 Numenta的规则首先要求计算推理值和基本事实之间的原始异常分数[2]。 原始异常分数计算仅仅是推理和地面实况之间的差异,然而,不考虑推理以上的点,因为我们只关注缺乏活动。 因此,我们的原始异常分数如下,其中f(x)是t时间t的预测,a是基本事实:
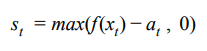
得到的一系列原始异常分数用于计算滚动均值和方差。 滚动平均值有两个窗口,其中W2的长度<W1。 两个滚动平均值和方差用于计算尾部概率,即最终异常似然分数。
PREDICTION MODELS 预测模型
- Hyperparameters 超参数
- Baseline (Threshold model) 基准模型
- Fourier Series 傅里叶系列
- DNN
- RNN
- LSTM
EXPERIMENT 实验
[待续…]


