二叉树遍历(递归+非递归)

二叉树的递归很简单，但是非递归就有点复杂了。

第一种先序遍历、中序遍历、第一种后序遍历都是一直将左子树压入栈，其中先序遍历和中序遍历输出位置不同，后序遍历则需要前驱标记pre来判断右孩子是否访问过；

第二种先序遍历和第二种后序遍历是根据层序遍历的思想写的，将队列换成栈，顺序换成先入右孩子再入左孩子，但是后序遍历需要用pre判断左右孩子是否都访问过。

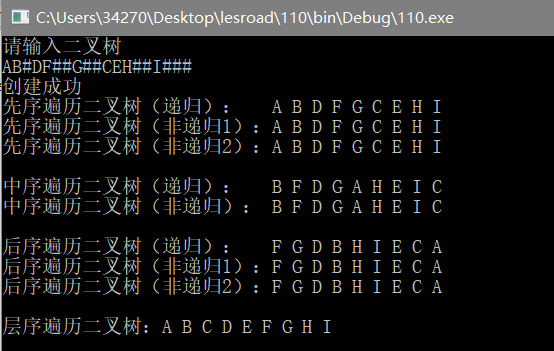
测试数据：AB#DF##G##CEH##I###

 

#include <bits/stdc++.h>
using namespace std;
struct node
{
    char data;
    node *l, *r;
};

//建立二叉树
void creat(node *&t)
{
    char c;
    cin>>c;
    if(c == '#')
    {
        t = NULL;
        return;
    }
    t = (node*)malloc(sizeof(node));
    t->data = c;
    creat(t->l);
    creat(t->r);
}

//先序遍历二叉树（递归）
void pre_di(node *t)
{
    if(!t) return;
    printf("%c ", t->data);
    pre_di(t->l);
    pre_di(t->r);
}

//中序遍历二叉树（递归）
void in_di(node *t)
{
    if(!t) return;
    in_di(t->l);
    printf("%c ", t->data);
    in_di(t->r);
}

//后序遍历二叉树（递归）
void post_di(node *t)
{
    if(!t) return;
    post_di(t->l);
    post_di(t->r);
    printf("%c ", t->data);
}

//先序遍历二叉树（非递归1）
void pre_no_di1(node *t)
{
    stack<node*>S;
    while(t || !S.empty())
    {
        if(t)
        {
            printf("%c ", t->data);
            S.push(t);
            t = t->l;
        }
        else
        {
            t= S.top();
            S.pop();
            t = t->r;
        }
    }
    cout<<endl;
}

//先序遍历二叉树（非递归2）
void pre_no_di2(node *t)
{
    stack<node*>S;
    S.push(t);
    while(!S.empty())
    {
        t = S.top();
        S.pop();
        printf("%c ", t->data);
        if(t->r) S.push(t->r);
        if(t->l) S.push(t->l);
    }
    cout<<endl;
}

//中序遍历二叉树（非递归）
void in_no_di(node *t)
{
    stack<node*>S;
    while(t || !S.empty())
    {
        if(t)
        {
            S.push(t);
            t = t->l;
        }
        else
        {
            t = S.top();
            S.pop();
            printf("%c ", t->data);
            t = t->r;
        }
    }
    cout<<endl;
}

//后序遍历二叉树（非递归1）
void post_no_di1(node *t)
{
    stack<node*>S;
    node *pre = NULL;
    while(t || !S.empty())
    {
        while(t)
        {
            S.push(t);
            t = t->l;
        }
        t = S.top();
        if(!t->r || pre == t->r)
        {
            printf("%c ", t->data);
            pre = t;
            S.pop();
            t = NULL;
        }
        else
            t = t->r;
    }
    cout<<endl;
}

//后序遍历二叉树（非递归2）
void post_no_di2(node *t)
{
    stack<node*>S;
    node *pre = NULL;//pre本来想写char类型，但是下面if里就要换成pre==t->l->data，如果t->l为空则会报错！
    S.push(t);
    while(!S.empty())
    {
        t = S.top();
        if((t->l == NULL && t->r == NULL) || (pre != NULL && (pre == t->l || pre == t->r))) //pre=t->l代表仅有左且已访问或者先访问过右又访问了左
        {
            printf("%c ", t->data);
            pre = t;
            S.pop();
        }
        else
        {
            if(t->r) S.push(t->r);
            if(t->l) S.push(t->l);
        }
    }
    cout<<endl;
}

//层序遍历
void ceng(node *t)
{
    queue<node*>Q;
    Q.push(t);
    while(!Q.empty())
    {
        t = Q.front();
        Q.pop();
        printf("%c ", t->data);
        if(t->l) Q.push(t->l);
        if(t->r) Q.push(t->r);
    }
    cout<<endl;
}

//销毁二叉树
void Free(node *&t)
{
    if(t->l) Free(t->l);
    if(t->r) Free(t->r);
    free(t);
}

int main()
{
    node *t;
    puts("请输入二叉树");
    creat(t);
    puts("创建成功");
    printf("先序遍历二叉树（递归）：   ");
    pre_di(t);
    cout<<endl;
    printf("先序遍历二叉树（非递归1）：");
    pre_no_di1(t);
    printf("先序遍历二叉树（非递归2）：");
    pre_no_di2(t);
    printf("\n中序遍历二叉树（递归）：   ");
    in_di(t);
    cout<<endl;
    printf("中序遍历二叉树（非递归）： ");
    in_no_di(t);
    printf("\n后序遍历二叉树（递归）：   ");
    post_di(t);
    cout<<endl;
    printf("后序遍历二叉树（非递归1）：");
    post_no_di1(t);
    printf("后序遍历二叉树（非递归2）：");
    post_no_di2(t);
    printf("\n层序遍历二叉树：");
    ceng(t);
    Free(t);
    return 0;
}

 

运行截图：