【hdu1705】Count the grid（皮克定理）
链接：http://acm.hdu.edu.cn/showproblem.php?pid=1705
【题意】
给出平面上三个点坐标，求围成的三角形内部的点数
做这道题需要先了解下皮克定理。
百度百科：皮克定理是指一个计算点阵中顶点在格点上的多边形面积公式，该公式可以表示为2S=2a+b-2，其中a表示多边形内部的点数，b表示多边形边界上的点数，s表示多边形的面积。
多边形边界上的整数点怎么求呢？
当然是gcd啦~~ gcd(x1-x2, y1-y2)就是这条边上整数点的个数。但是仅仅一条边是不准确的（有一个端点没有算上），需要把所有边的gcd加上才是皮克定理中的「b」。
面积怎么求呢？
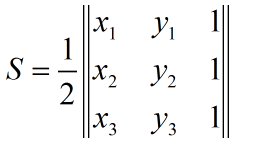
然后就可以开心地求出a啦~
1 #include <bits/stdc++.h> 2 using namespace std; 3 typedef long long LL; 4 struct q 5 { 6 LL x, y; 7 } co[5]; 8 LL area() 9 { 10 return abs(co[1].x*(co[2].y-co[3].y)-co[1].y*(co[2].x-co[3].x)+co[2].x*co[3].y-co[3].x*co[2].y);//算出来可能为负数，所以abs 11 } 12 LL gcd(LL a, LL b) 13 { 14 if(a < b) swap(a, b); //a如果小于b的话要交换位置 15 if(b == 0) return a; 16 return gcd(b,a%b); 17 } 18 int main() 19 { 20 while(1) 21 { 22 scanf("%lld%lld%lld%lld%lld%lld", &co[1].x, &co[1].y, &co[2].x, &co[2].y, &co[3].x, &co[3].y); 23 if(co[1].x==0&&co[1].y==0&&co[2].x==0&&co[2].y==0&&co[3].x==0&&co[3].y==0) break; 24 double s = area() / 2.0; 25 LL ab = gcd(abs(co[1].x - co[2].x), abs(co[1].y - co[2].y)); 26 LL bc = gcd(abs(co[2].x - co[3].x), abs(co[2].y - co[3].y)); 27 LL ac = gcd(abs(co[1].x - co[3].x), abs(co[1].y - co[3].y)); 28 LL in = s - (ab + bc + ac) / 2.0 + 1; 29 printf("%lld\n", in); 30 } 31 return 0; 32 }
