1维FDTD仿真
FDTD基本原理是把麦克斯韦方程胡两个矢量旋度方程写成差分形式,利用数值方法求其解。
假设电磁场传播方向为x轴方向,电场只有z轴方法分量,磁场只有y轴方向分量。两个旋度方程可以写成下列形式
电场、磁场写成下在形式
连续方程写成差分形式
其中的常数项因子
实现时可用下图表示
从而得到差分递推方程如下
hy(mm) = hy(mm) + (ez(mm+1)- ez(mm))/imp0;
ez(mm) = ez(mm) + (hy(mm)- hy(mm-1))*imp0;%1D FDTD with source
SIZE = 200;
ez = zeros(1,SIZE);
hy = zeros(1,SIZE);
imp0=377.0;
maxTime = 10000;
for qTime = 0 : 1 : maxTime
for mm = 1 : 1 : SIZE -1
hy(mm) = hy(mm) + (ez(mm+1)- ez(mm))/imp0;
end
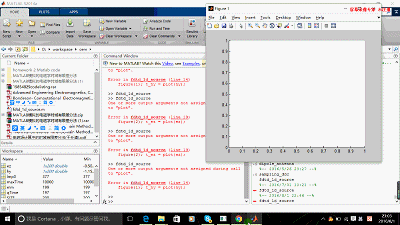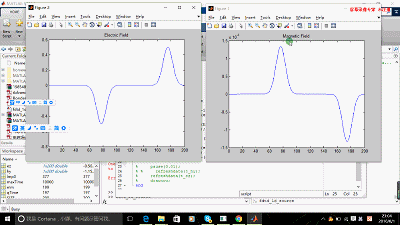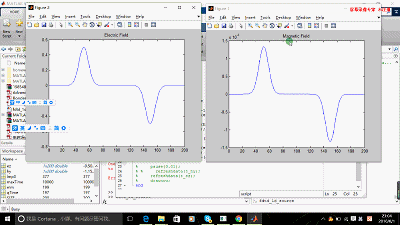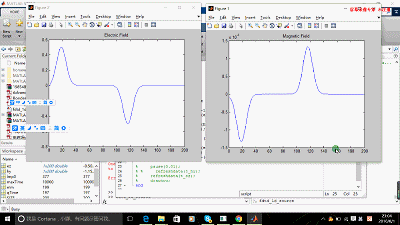
figure(1); t_hy = plot(hy);
title('Magnetic Field');
for mm = 2 : 1 : SIZE
ez(mm) = ez(mm) + (hy(mm)- hy(mm-1))*imp0;
end
figure(2); t_ez = plot(ez);
title('Electric Field')
ez(50) = ez(50) + exp(-(qTime-30.0)*(qTime-30.0)/100.0);
% pause(0.01);
% % refreshdata(t_hy);
% refreshdata(t_ez);
% drawnow;
end