记-CNN中的激活函数
1.概念
激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数,那么该网络仅能够表达线性映射,此时即便有再多的隐藏层,其整个网络跟单层神经网络也是等价的。因此也可以认为,只有加入了激活函数之后,深度神经网络才具备了分层的非线性映射学习能力。
2.特性
可微性: 当优化方法是基于梯度的时候,这个性质是必须的。
单调性: 当激活函数是单调的时候,单层网络能够保证是凸函数。
输出值的范围: 当激活函数输出值是 有限 的时候,基于梯度的优化方法会更加 稳定,因为特征的表示受有限权值的影响更显著;当激活函数的输出是 无限 的时候,模型的训练会更加高效,不过在这种情况小,一般需要更小的learning rate
3.作用
在我们面对线性可分的数据集的时候,简单的用线性分类器即可解决分类问题。但是现实生活中的数据往往不是线性可分的,面对这样的数据,一般有两个方法:引入非线性函数、线性变换
4.使用场景
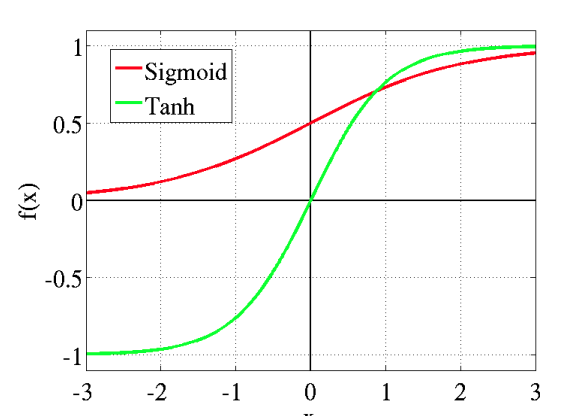
(1)Sigmoid
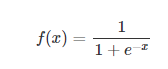
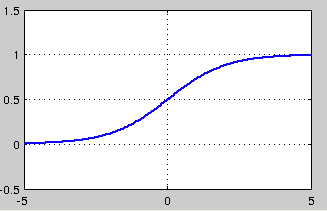
sigmoid 是使用范围最广的一类激活函数,具有指数函数形状,它在物理意义上最为接近生物神经元。此外,(0, 1) 的输出还可以被表示作概率,或用于输入的归一化,代表性的如Sigmoid交叉熵损失函数。
可以看出,sigmoid函数连续,光滑,严格单调,以(0,0.5)中心对称,是一个非常良好的阈值函数。
当x趋近负无穷时,y趋近于0;趋近于正无穷时,y趋近于1;x=0时,y=0.5。当然,在x超出[-6,6]的范围后,函数值基本上没有变化,值非常接近,在应用中一般不考虑。
Sigmoid函数的值域范围限制在(0,1)之间,我们知道[0,1]与概率值的范围是相对应的,这样sigmoid函数就能与一个概率分布联系起来了。
Sigmoid函数的导数是其本身的函数,即f′(x)=f(x)(1−f(x))f′(x)=f(x)(1−f(x)),计算非常方便,也非常节省计算时间。
然而,sigmoid也有其自身的缺陷,最明显的就是饱和性。从上图可以看到,其两侧导数逐渐趋近于0
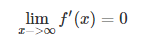
具有这种性质的称为软饱和激活函数。具体的,饱和又可分为左饱和与右饱和。与软饱和对应的是硬饱和, 即
sigmoid 的软饱和性,使得深度神经网络在二三十年里一直难以有效的训练,是阻碍神经网络发展的重要原因。具体来说,由于在后向传递过程中,sigmoid向下传导的梯度包含了一个 f′(x)f′(x) 因子(sigmoid关于输入的导数),因此一旦输入落入饱和区,f′(x)f′(x) 就会变得接近于0,导致了向底层传递的梯度也变得非常小。此时,网络参数很难得到有效训练。这种现象被称为梯度消失。一般来说, sigmoid 网络在 5 层之内就会产生梯度消失现象
此外,sigmoid函数的输出均大于0,使得输出不是0均值,这称为偏移现象,这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。
(2)tanh
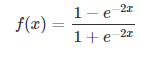

tanh也是一种非常常见的激活函数。与sigmoid相比,它的输出均值是0,使得其收敛速度要比sigmoid快,减少迭代次数。然而,从途中可以看出,tanh一样具有软饱和性,从而造成梯度消失
(3)ReLU,P-ReLU, Leaky-ReLU
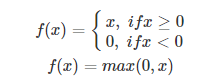
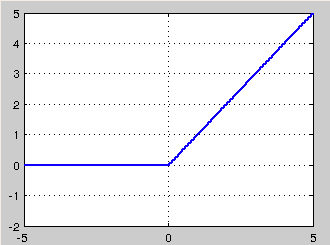
ReLU的全称是Rectified Linear Units,是一种后来才出现的激活函数。 可以看到,当x<0时,ReLU硬饱和,而当x>0时,则不存在饱和问题。所以,ReLU 能够在x>0时保持梯度不衰减,从而缓解梯度消失问题。这让我们能够直接以监督的方式训练深度神经网络,而无需依赖无监督的逐层预训练。
然而,随着训练的推进,部分输入会落入硬饱和区,导致对应权重无法更新。这种现象被称为“神经元死亡”。与sigmoid类似,ReLU的输出均值也大于0,偏移现象和 神经元死亡会共同影响网络的收敛性。
针对在x<0的硬饱和问题,我们对ReLU做出相应的改进,使得
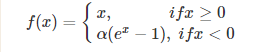
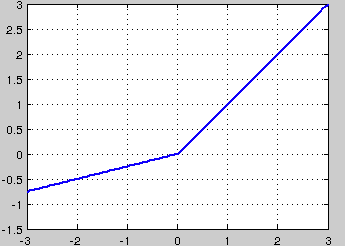
这就是Leaky-ReLU, 而P-ReLU认为,αα也可以作为一个参数来学习,原文献建议初始化a为0.25,不采用正则。
(4)ELU

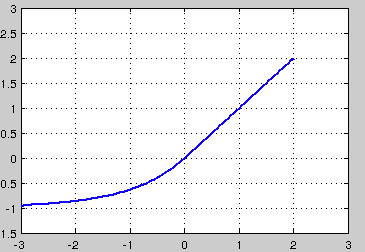
融合了sigmoid和ReLU,左侧具有软饱和性,右侧无饱和性。右侧线性部分使得ELU能够缓解梯度消失,而左侧软饱能够让ELU对输入变化或噪声更鲁棒。ELU的输出均值接近于零,所以收敛速度更快。在 ImageNet上,不加 Batch Normalization 30 层以上的 ReLU 网络会无法收敛,PReLU网络在MSRA的Fan-in (caffe )初始化下会发散,而 ELU 网络在Fan-in/Fan-out下都能收敛
(5)Maxout
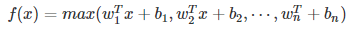
Maxout模型实际上也是一种新型的激活函数,在前馈式神经网络中,Maxout的输出即取该层的最大值,在卷积神经网络中,一个Maxout feature map可以是由多个feature map取最值得到。
maxout的拟合能力是非常强的,它可以拟合任意的的凸函数。但是它同dropout一样需要人为设定一个k值。
为了便于理解,假设有一个在第i层有2个节点第(i+1)层有1个节点构成的神经网络。
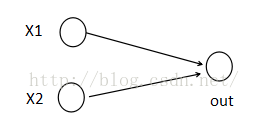
激活值 out = f(W.X+b); f是激活函数。’.’在这里代表內积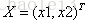
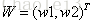
那么当我们对(i+1)层使用maxout(设定k=5)然后再输出的时候,情况就发生了改变。
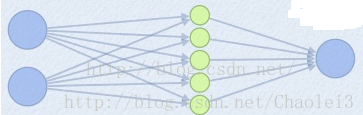
此时网络形式上就变成上面的样子,用公式表现出来就是:
z1 = W1.X+b1;
z2 = W2.X+b2;
z3 = W3.X+b3;
z4 = W4.X+b4;
z5 = W4.X+b5;
out = max(z1,z2,z3,z4,z5);
也就是说第(i+1)层的激活值计算了5次,可我们明明只需要1个激活值,那么我们该怎么办?其实上面的叙述中已经给出了答案,取这5者的最大值来作为最终的结果。
总结一下,maxout明显增加了网络的计算量,使得应用maxout的层的参数个数成k倍增加,原本只需要1组就可以,采用maxout之后就需要k倍了。
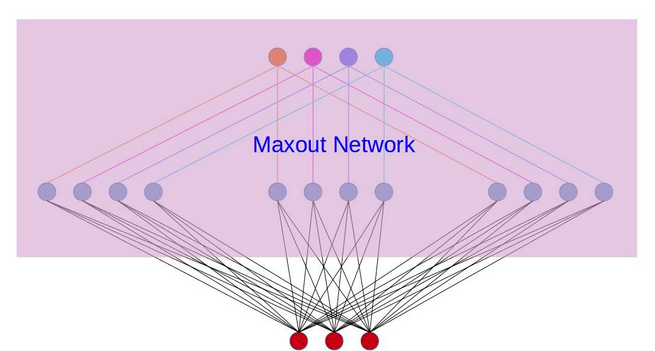
再叙述一个稍微复杂点的应用maxout的网络,网络图如下:



 浙公网安备 33010602011771号
浙公网安备 33010602011771号