中序线索二叉树

　　虽说对于二叉树的遍历操作来说非递归法使用用户自定义的栈来代替递归使用时的系统栈，可以得到不小的效率提升，但将二叉树线索化时能将用户栈也省略掉进一步提高了效率。

　　对于二叉树的链表结构，n个结点的二叉树有n+1个空链域（每个叶节点都有两个空链域），而线索二叉树就把这些空链域有效的利用了起来，在一般的二叉树中，我们只知道每个结点的左右孩子，并不知道某个结点在某种遍历方式下的直接前驱和直接后继，如果能够知道前驱和后继信息，就可以把二叉树看作一个链表结构，从而可以像遍历链表那样来遍历二叉树，进而提高效率。这对经常需要进行遍历操作的二叉树而言，无疑是很有用的。

　 （1）中序线索二叉树的构造

　　线索二叉树的结点结构如下：

lchild

ltag

data

rtag

rchild

　　在二叉树线索化的过程中会把原有的空指针利用起来作为寻找当前结点的前驱或者后继的线索，但是这样的话，线索和树中原有指向孩子结点的指针分不清，于是给左右孩子结点添加标记（itag、rtag），即：

　　如果ltag=0，表示lchild为指向孩子结点的指针，如果ltag=1，则表示lchild为线索，指向结点的前驱；

　　如果rtag=0，表示rchild为指向孩子结点的指针，如果rtag=1，则表示rchild为线索，指向结点的后继；

　　结点定义如下：

typedef struct TBTNode{
    char data;
    int ltag,rtag;
    struct TBTNode *lchild;
    struct TBTNode *rchild;
}TBTNode;

　　线索化的规则是：左线索指针指向当前结点在中序遍历序列中的前驱结点，右线索指针指向后继结点。因此我们需要一个指针p指向当前正在访问的结点，pre指向p的前驱结点，p的左线索指针如果存在的话直接指向pre（也就是前驱结点），pre的右线索如果存在则指向p（也就是直接后继）。

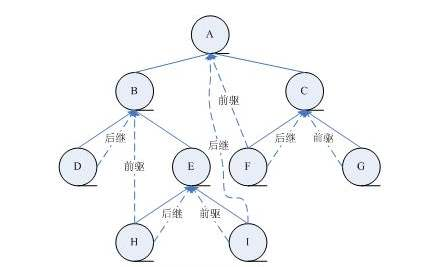
　　如图，中序遍历序列为DBHEIAFCG，所以从序列中我们可以直接得出H的前驱为B后继为E，I的前驱为E后继为A等等。

void InThread(TBTNode *p, TBTNode *&pre){
    if (p != null)
    {
        InThread(p->lchild, pre);    //对左孩子递归，自然第一个操作的结点为最左下结点（不一定为叶结点），如上图为D
        if (p->lchild == NULL)
        {
            p->lchild = pre;
            p->ltag = 1;
        }
        if (pre != NULL && pre->rchild == NULL)
        {
            pre->rchild = p;
            pre->rtag = 1;
        }
        pre = p; //当p将要离开一个访问过的结点时，pre指向p，所以p指向新结点时，pre显然是此时p的直接前驱
        p = p->rchild; //p指向右孩子，准备将右子树线索化
        InThread(p, pre);
    }
}

　　（2）遍历中序线索二叉树

TBTNode *First(TBTNode *p){//寻找中序序列下第一个结点
    while(p->ltag == 0)
        p=p->lchild;
    return p; //寻找树的最左下角结点（不一定是叶节点，如上图树中是D
}

TBTNode *Next(TBTNode *p){
    if (p->tag == 0)
        return First(p->rchild); //中序遍历下，p结点的下一个结点自然是p的右子树中First()求出来的结点
    else
        return p->rchild; //rtag==1，此时rchild为线索，指向结点的直接后继
}

void InOrder(TBTNode *root){//遍历
    for (TBTNode *p = First(root) ; p !=NULL ; p = Next(p))
    {
        //对结点操作
    }
}