期权定价的BS公式

期权定价的BS公式是指由Black-Scholes模型提出的期权定价公式，它是一种用于计算欧式期权价格的数学模型。BS公式的全称是Black-Scholes-Merton公式，它是由费希尔·布莱克（Fischer Black）、默顿·斯科尔斯（Myron Scholes）和罗伯特·默顿（Robert Merton）在1973年独立提出的。

BS公式的基本形式如下：

C=St​N(d1​)−Xe−r(T−t)N(d2​)

P=Xe−r(T−t)N(−d2​)−St​N(−d1​)

其中：

St​：当前标的资产（如股票）价格。

X：期权的行权价格。

T：期权的到期日。

t：当前时间。

r：无风险利率。

N(⋅)：标准正态分布的累积分布函数。

d1​ 和 d2​ 是计算中间变量，分别为：

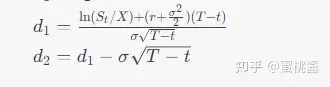
​其中，σ 是标的资产的波动率（年化波动率）。

BS公式的前提假设了市场是有效的，标的资产的价格服从几何布朗运动，并且不存在交易成本、无风险利率是恒定的等。这个公式在金融领域被广泛应用，为期权交易提供了重要的理论基础。

一、用VBA代码书写上述过程：

Function BlackScholes(OptionType As String, S As Double, X As Double, T As Double, r As Double, Volatility As Double) As Double
    Dim d1 As Double
    Dim d2 As Double
    
    ' 计算d1和d2
    d1 = (Log(S / X) + (r + (Volatility ^ 2) / 2) * T) / (Volatility * Sqr(T))
    d2 = d1 - Volatility * Sqr(T)
    
    ' 根据期权类型计算期权价格
    If OptionType = "Call" Then
        BlackScholes = S * WorksheetFunction.NormSDist(d1) - X * Exp(-r * T) * WorksheetFunction.NormSDist(d2)
    ElseIf OptionType = "Put" Then
        BlackScholes = X * Exp(-r * T) * WorksheetFunction.NormSDist(-d2) - S * WorksheetFunction.NormSDist(-d1)
    Else
        ' 如果期权类型不是"Call"或"Put"，返回错误值
        BlackScholes = CVErr(xlErrValue)
    End If
End Function

此代码定义了一个名为BlackScholes的VBA函数，该函数接受期权类型（"Call"或"Put"）、标的资产价格（S）、行权价格（X）、剩余到期时间（T）、无风险利率（r）和波动率（Volatility）作为输入参数，并返回期权的理论价格。

你可以将此VBA代码添加到Excel工作簿的Visual Basic for Applications编辑器中（按ALT+F11），然后在Excel中使用BlackScholes函数来计算期权价格。例如，如果你要计算一个看涨期权的价格，可以使用以下公式：

=BlackScholes("Call", S, X, T, r, Volatility)

其中，S、X、T、r和Volatility分别是你的标的资产价格、行权价格、剩余到期时间、无风险利率和波动率的Excel单元格引用。同样，如果你要计算看跌期权的价格，只需将"Call"替换为"Put"。

 

二、用python写上述代码：

import numpy as np
from scipy.stats import norm

def black_scholes(option_type, S, X, T, r, volatility):
    d1 = (np.log(S / X) + (r + 0.5 * volatility ** 2) * T) / (volatility * np.sqrt(T))
    d2 = d1 - volatility * np.sqrt(T)
    
    if option_type == "Call":
        option_price = S * norm.cdf(d1) - X * np.exp(-r * T) * norm.cdf(d2)
    elif option_type == "Put":
        option_price = X * np.exp(-r * T) * norm.cdf(-d2) - S * norm.cdf(-d1)
    else:
        raise ValueError("Invalid option type")
    
    return option_price

# 示例数据
option_type = "Call"  # 期权类型，可以是"Call"或"Put"
S = 100  # 标的资产的当前价格
X = 105  # 期权的行权价格
T = 0.5  # 剩余到期时间（以年为单位）
r = 0.05  # 无风险利率
volatility = 0.2  # 波动率

# 计算期权价格
option_price = black_scholes(option_type, S, X, T, r, volatility)
print(f"Option Price: {option_price}")

 

知道C和P的前提下，怎么计算波动率？

如果你知道期权的价格（C和P）、标的资产的当前价格（S）、行权价格（X）、剩余到期时间（T）、无风险利率（r），并且想要计算波动率（Volatility），你可以使用Black-Scholes模型的反向计算方法，通常称为隐含波动率计算。

Black-Scholes模型中的波动率是一个未知数，但可以通过反向计算来估算出来，以使模型产生已知的期权价格。以下是计算隐含波动率的一种常见方法，使用二分法或牛顿-拉普森法（Newton-Raphson method）：

1. 首先，你需要编写一个函数，该函数以波动率作为输入，并使用Black-Scholes模型来计算期权价格（C或P）。这个函数将返回期权价格与市场观察到的实际价格之间的差异（误差）。

2. 接下来，你可以使用二分法或牛顿-拉普森法来找到使上述误差最小化的波动率值。这个波动率值就是隐含波动率。

以下是一个简化的示例，使用二分法来计算隐含波动率的过程：

用VBA代码：

Function ImpliedVolatility(OptionType As String, S As Double, X As Double, T As Double, r As Double, MarketPrice As Double) As Double
    Dim lowVolatility As Double
    Dim highVolatility As Double
    Dim tolerance As Double
    Dim currentVolatility As Double
    
    lowVolatility = 0.01 ' 设置波动率的下限
    highVolatility = 3.0 ' 设置波动率的上限
    tolerance = 0.0001 ' 设置误差容忍度
    
    Do While highVolatility - lowVolatility > tolerance
        currentVolatility = (lowVolatility + highVolatility) / 2 ' 取中值作为当前波动率估计
        
        ' 使用当前波动率计算期权价格
        Dim OptionPrice As Double
        OptionPrice = BlackScholes(OptionType, S, X, T, r, currentVolatility)
        
        ' 检查期权价格与市场价格的差异，然后相应地调整波动率的上限或下限
        If OptionPrice < MarketPrice Then
            lowVolatility = currentVolatility
        Else
            highVolatility = currentVolatility
        End If
    Loop
    
    ' 返回隐含波动率
    ImpliedVolatility = currentVolatility
End Function

 

用python代码：

import numpy as np
from scipy.stats import norm
from scipy.optimize import brentq

def black_scholes(option_type, S, X, T, r, volatility):
    d1 = (np.log(S / X) + (r + 0.5 * volatility ** 2) * T) / (volatility * np.sqrt(T))
    d2 = d1 - volatility * np.sqrt(T)
    
    if option_type == "Call":
        option_price = S * norm.cdf(d1) - X * np.exp(-r * T) * norm.cdf(d2)
    elif option_type == "Put":
        option_price = X * np.exp(-r * T) * norm.cdf(-d2) - S * norm.cdf(-d1)
    else:
        raise ValueError("Invalid option type")
    
    return option_price

def implied_volatility(option_type, S, X, T, r, market_price):
    # Define a function to minimize (the difference between market and model prices)
    def func(volatility):
        return black_scholes(option_type, S, X, T, r, volatility) - market_price
    
    # Find the implied volatility using the Brent method
    implied_volatility = brentq(func, 0.01, 3.0)  # You can adjust the bounds as needed
    
    return implied_volatility

# Example data
option_type = "Call"
S = 100
X = 105
T = 0.5
r = 0.05
market_price = 10

# Calculate implied volatility
iv = implied_volatility(option_type, S, X, T, r, market_price)
print(f"Implied Volatility: {iv}")