VAR算法介绍

1. 风险价值（VaR）简述
风险价值（value at risk，VaR）是指在一定的持有期和给定的置信水平下，利率、汇率、股价等风险因子发生变化时可能对投资组合造成的潜在最大损失。例如：持有期 1 天、置信水平 95% 的情况下，计算得到的 VaR 值为 1000 万元，则表明该投资组合在1天中有 95%的可能性损失不会超过1000万，换句话说，1 天中，有5%的可能性损失会超过 1000 万元。

VaR的大小取决于两个参数：持有期（N）、置信水平（X）。由于 VaR 度量的是投资组合的亏损，其对应于投资组合盈亏分布的左端尾部，为了表述方便，通常 VaR 值用绝对值表示。

VaR 的数学表达式如下：

 

 

 根据巴塞尔协议的明确规定：银行需要计算持有期10天、置信水平99%的VaR。在实际计算中，通常先计算 N=1 时的VaR，在计算相同置信水平下 N>1 时的 VaR，其表达式如下：

 

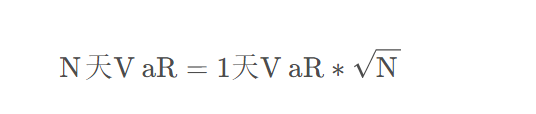
 上式成立的条件是：投资组合价值在不同交易日之间的变化是相互独立并服从期望值为0的相同正态分布，其他情况下，该等式只是一个近似值。

2.方差-协方差法

数学假定：

• 1 投资组合的各风险因子服从联合正态分布
• 2 线性假定，持有期内，投资组合的风险暴露与风险因子之间是线性相关的

其表达式如下：

 

假定不管是过去的收益率R还是未来的收益率R，都是独立同分布的。所以方差—协方差法借助历史数据来估计未来收益率R的分布。而且，方差—协方差法事先假定R服从某一具体分布，如正态分布;但是该分布函数的所有参数还是未知的，如，正态分布的均值μ，方差σ2。假如现在我们收集了n个收益率R的数据：Ri，i=1,2，…，ni=1,2，…，n，那么我们可用这些历史数据来估计参数。通过参数估计，我们获得了R的概率密度函数f（x）和分布函数F（x）。根据R∗的定义（置信水平p下，未来持有期T的最小收益率），用数学语言表示如下：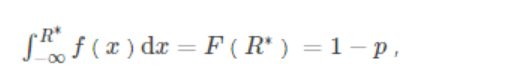

 

 

则我们要找的R∗等于：R的概率分布的下分位数Z1−p, 如下图的白色部分； 特殊分布可通过查表求得该下分位数Z1−p，

数学公式可表示： （R* - μ）/σ = Z1−p

e.g 标准正态分布下的概率密度图：

 

 

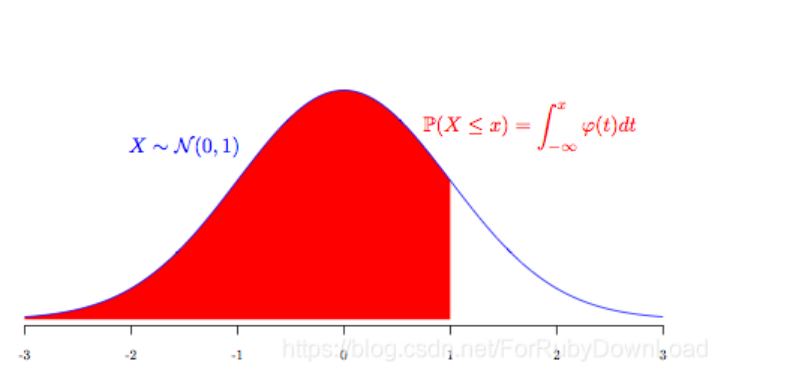
参考案例：
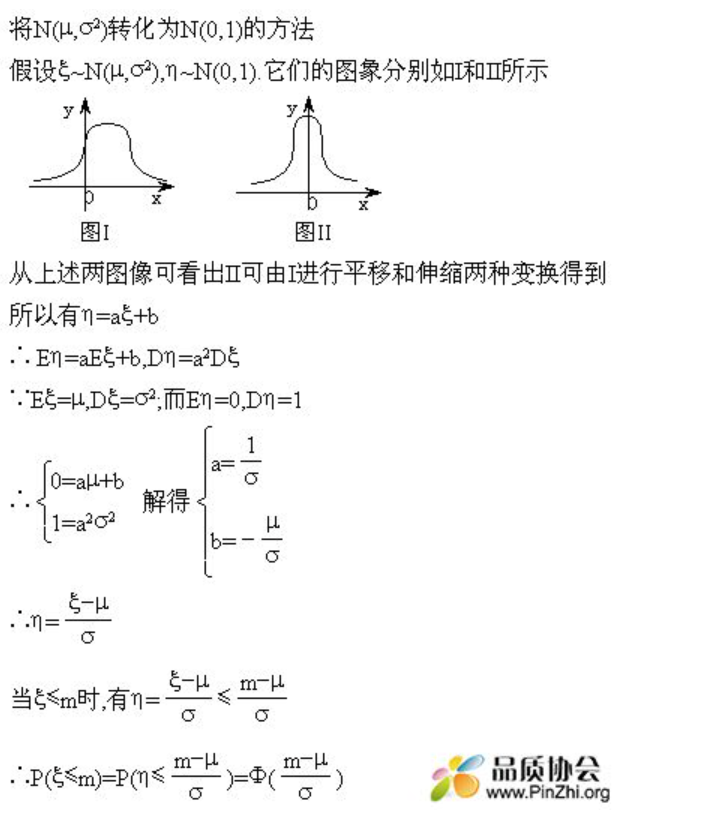
基金A的期初价值为V0=1000万万，假定其服从正态分布，根据收集到的历史收益率（持有期为10天），估计出RR~N（0.1,0.04）， 假定置信水平p=p=99%， 求VaR。其实该题等价于求解正太分布X-N(u, σ2)曲线下， 覆盖面值99%所对应的分位数（Z-Score）, 可把非标准正态分布转换成正太分布（x-u）/σ.

 

 计算结果表明：在未来10天，期初价值为1000万的基金A的绝对损失大于366万的概率不超过1%。