最大回撤计算--基于python

一、指标介绍

最大回撤率：是指在选定周期内任一历史时点往后推，产品净值走到最低点时的收益率回撤幅度的最大值。最大回撤用来描述买入产品后可能出现的最糟糕的情况。最大回撤是一个重要的风险指标，对于对冲基金和数量化策略交易，该指标比波动率还重要。

.回撤用来衡量该私募产品的抗风险能力。

回撤的意思，是指在某一段时期内产品净值从最高点开始回落到最低点的幅度

最大回撤率，不一定是（最高点净值-最低点净值）/最高点时的净值，也许它会出现在其中某一段的回落。

公式可以这样表达：

D为某一天的净值，i为某一天，j为i后的某一天，Di为第i天的产品净值，Dj则是Di后面某一天的净值

drawdown就是最大回撤率

drawdown=max（（Di-Dj）/Di），其实就是对每一个净值进行回撤率求值，然后找出最大的。可以使用程序实现。

二、程序实现：

导入数据：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.style.use("seaborn") #图形网格效果
data = pd.read_excel("aaa.xlsx",index_col=[0],parse_dates=[0])
data 

结果：

 

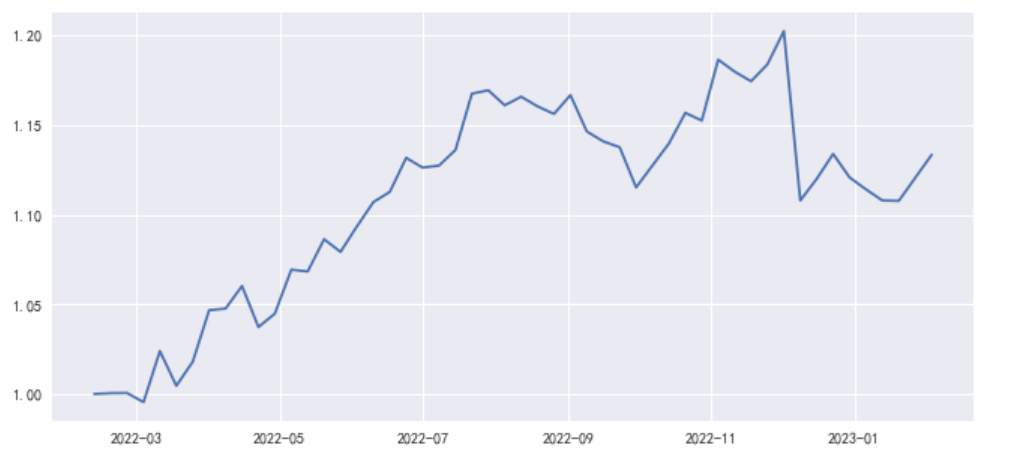
收盘价走势 绘图：

plt.figure(figsize=(11,5))
plt.plot(data['close'])

 

 最大回撤计算方法：

i = np.argmax((np.maximum.accumulate(data['close']) - data['close'])) # 最大回撤结束的位置 最低的那个位置 np.argmax作用：取出数组中最大值对应的索引
if i == 0:
    j = 0
else:
    j = np.argmax(data['close'][:i])  # 回撤开始的位置 最高的那个点
maxdrawdown = data['close'][j] - data['close'][i] # 最大回撤
maxdrawdown_rate = (data['close'][j] - data['close'][i]) / data['close'][j] # 最大回撤率
drawdown_days = i - j # 回撤持续天数

 

 三、最大回撤可视化：

plt.rcParams['font.sans-serif']=['SimHei']  #显示汉字
start_DAY = data.index[i] #开始回撤的日期
end_DAY = data.index[j] #结束回撤的日期
start_net_value = data[data.index == start_DAY]['close'].values[0] #开始回撤的净值
end_net_value = data[data.index == end_DAY]['close'].values[0] #结束回撤的净值
plt.figure(figsize=(11,5))
plt.plot(data['close'],color='b')
plt.plot([start_DAY, end_DAY], [start_net_value, end_net_value], linestyle='--', label="最大回撤",color='r')
plt.legend()