[HNOI2008][bzoj 1005]明明的烦恼（prufer序列）

1005: [HNOI2008]明明的烦恼

Time Limit: 1 Sec  Memory Limit: 162 MB
Submit: 7121  Solved: 2816
[Submit][Status][Discuss]

Description

　　自从明明学了树的结构,就对奇怪的树产生了兴趣......给出标号为1到N的点,以及某些点最终的度数,允许在
任意两点间连线,可产生多少棵度数满足要求的树?

Input

　　第一行为N(0 < N < = 1000),
接下来N行,第i+1行给出第i个节点的度数Di,如果对度数不要求,则输入-1

Output

　　一个整数,表示不同的满足要求的树的个数,无解输出0

Sample Input

3
1
-1
-1

Sample Output

2

HINT

　　两棵树分别为1-2-3;1-3-2

题解：

树的计数题目，可以想到是用prufer序列来求解。

先来科普一下prufer的性质：

1. 每个prufer序列都唯一对应着一棵树。
2. prufer序列的长度等于它所对应的树的节点数-2。
3. 每个数在prufer序列中出现的次数等于该节点在树中的度数-1。

其实有了这些性质我们就可以做题了（想要证明的自行度娘），现在我们在来观察一下这道题，如果他给出的是所有点的度数，那么这道题就是一个不全相异的全排列个数（戳这里），但是他给出的点的度数只是一部分的，那我们就可以先当别的点不存在，先把这一部分的方案数求出来，设$tot=\Sigma{d[i]-1}$,$tot$即为已经确定度数的点在prufer序列里所占的个数，这一部分方案数为$C_{n-2}^{tot}$,但是别忘了我们还要处理重复的部分，处理第一个数向$tot$个数中插的方案数为$C_{tot}^{d[1]-1}$,同理处理第二个数的方案数是$C_{tot-(d[1]-1)}^{d[2]-1}$,剩下的以此类推。

但是别忘了我们还有没确定度数的点，但是这很好处理，我们设未确定的点数为$cnt$，这就相当于在$n-2-tot$的空间中随便选$cnt$个，那么答案即为$cnt^{n-2-tot}$

然后我们根据乘法原理可以的出答案

$ans=C_{n-2}^{tot}*C_{tot}^{d[1]-1}*C_{tot-(d[1]-1)}^{d[2]-1}*\cdots*C_{d[i]-1}^{d[i]-1}*cnt^{n-2-tot}$

我们把组合数公式展开来一波化简就得到了结果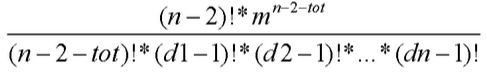（数学公式崩了，凑或者看吧qwq）

这样再用一个高精就阔以了。

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<vector>
using namespace std;
#define int long long
const int N=500005;
int d[N];
struct BigInt{
    int m[N];
    friend void operator *= (BigInt &a,int b){
        int x=0;
        for(int i=1;i<=a.m[0];i++){
            int y=a.m[i]*b+x;
            a.m[i]=y%10;
            x=y/10;
        }
        while(x){
            a.m[++a.m[0]]=x%10;
            x/=10;
        }
    }
    friend void operator /= (BigInt &a,int b){
        int x=0;
        for(int i=a.m[0];i>=1;i--){
            x+=a.m[i];
            a.m[i]=x/b;
            x%=b;
            x*=10;
        }
        while(a.m[a.m[0]]==0&&a.m[0]>1) a.m[0]--;
    }
    friend void print(BigInt a){
        for(int i=a.m[0];i>=1;i--) printf("%lld",a.m[i]);
        puts("");
    }
}x;
signed main(){
    int n;
    scanf("%lld",&n);
    x.m[0]=x.m[1]=1;
    int cnt=0,num=0;
    if(n==1){
        int k;
        scanf("%lld",&k);
        if(!k){puts("0");}
        else puts("1");
        return 0;
    }
    for(int i=1;i<=n;i++){
        int mm;
        scanf("%lld",&mm);
        if(!mm){puts("0");return 0;}
        if(mm==-1) cnt++;
        else {d[i]=mm-1;num+=d[i];}
    }
    for(int i=1;i<=n-2;i++) x*=i;
    //for(int i=1;i<=num;i++) x*=i;
    //for(int i=2;i<=/*n-cnt-2*/num;i++) x*=i;
    for(int i=1;i<=n-2-num;i++) x*=cnt,x/=i;
    for(int i=1;i<=n;i++){
        if(d[i]>0){
            for(int j=1;j<=d[i];j++) x/=j; 
        }
    }
    print(x);
}