B-spline Basis Functions:Definition B样条基函数的定义

　本博客转自前人的博客的翻译版本，前几章节是原来博主的翻译内容，但是后续章节博主不在提供翻译，后续章节我在完成相关的翻译学习。

　（原来博客网址：http://blog.csdn.net/tuqu/article/details/4749586）

　原来的博主翻译还是很好的，所以前几章节直接借鉴参考原博主的内容。

 

B-spline Basis Functions:Definition

　　贝塞尔基函数用作权重。B-样条基函数也一样；但更复杂。但是它有两条贝塞尔基函数所没有的特性，即(1)定义域被节点细分（subdivided）； (2) 基函数不是在整个区间非零。实际上，每个B样条基函数在附近一个子区间非零，因此，B-样条基函数相当“局部”。

　　设U 是m + 1个非递减数的集合，u₀ <= u₂ <= u₃ <= ... <= u_m。u_i称为节点（knots）, 集合U 称为节点向量（knot vector）, 半开区间[u_i, u_i+1) 是第i个节点区间（knot span）。注意某些u_i可能相等，某些节点区间会不存在。如果一个节点 u_i 出现 k 次 (即，u_i = u_i+1 = ... = u_i+k-1), 其中 k > 1, u_i 是一个重复度（multiplicity）为k 的多重节点，写为 u_i(k)。 否则，如果u_i只出现一次，它是一个简单节点。如果节点等间距(即， u_i+1 - u_i 是一个常数，对 0 <= i <= m - 1)，节点向量或节点序列称为均匀的；否则它是非均匀的。

　  节点可认为是分隔点，将区间[u₀, u_m]细分为节点区间。所有B-样条基函数被假设定义域在[u₀, u_m]上。在本文中，我们经常使用u₀ = 0和u_m = 1，所以定义域是闭区间[0,1]。

　  为了定义B-样条基函数，我们还需要一个参数，基函数的次数（degree）p，第i个p次B-样条基函数，写为N_i,p(u)，递归定义如下：

　　　　

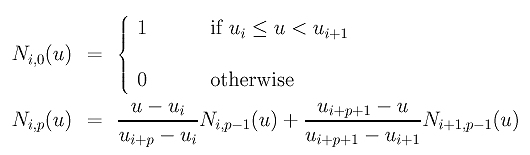
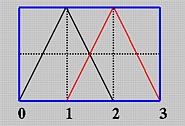
　　 上述公式通常称为Cox-de Boor递归公式。 这个定义看起来很复杂；但是不难理解。如果次数（degree）为零（即， p = 0），这些基函数都是阶梯函数，这也是第一个表达式所表明的。即，如果u是在第i个节点区间[u_i, u_i+1)上基函数N_i,0(u)是1。 例如，如果我们有四个节点u₀ = 0, u₁ = 1, u₂ = 2和 u₃ = 3, 节点区间 0, 1 和2是[0,1), [1,2), [2,3)，0次基函数是N_0,0(u) = 1 在 [0,1) ，在其它区间是0；N_1,0(u) = 1 在 [1,2)上，在其它区间是0；N_2,0(u) = 1在[2,3)上，其它区间是0。如下图所示：

　　

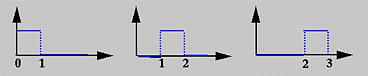
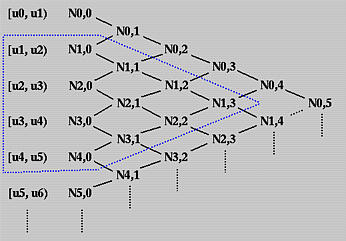
　　   为了理解p大于0时计算N_i,p(u)的方法，我们使用三角计算格式。所有节点区间列在左边（第一）列，所有零次基函数在第二列。见下图。

　　

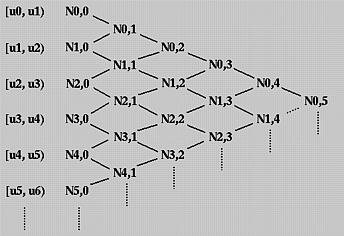
　　  为了计算N_i,1(u)，需要N_i,0(u)和N_i+1,0(u)。因此，我们可以计算N_0,1(u), N_1,1(u), N_2,1(u), N_3,1(u) 等等。所有这些N_i,1(u)写在第三列。一旦所有N_i,1(u)计算完毕，我们可以计算N_i,2(u)并将其放在第四列。继续这个过程直到所有需要的N_i,p(u)的计算完毕。

　　 上面我们获得了针对节点向量 U = { 0, 1, 2, 3 }的N_0,0(u), N_1,0(u)和N_2,0(u) 。现在计算N_0,1(u)和N_1,1(u)。要计算N_0,1(u)，因为i = 0和p = 1，从定义出发有

　　

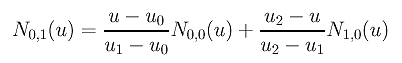
　　因为u₀ = 0, u₁ = 1和u₂ = 2,上式变为

　　

　　因为N_0,0(u)在[0,1)上非零且N_1,0(u)在[1,2)上非零，如果u在[0,1)上 (resp., [1,2) ), 只有N_0,0(u) (resp., N_1,0(u) )对N_0,1(u)有贡献。因此，如果u 在[0,1)上, N_0,1(u) 是uN_0,0(u) = u而如果u 在[1,2)上, N_0,1(u)是 (2 - u)N_1,0(u) = (2 - u)。相似的计算得到N_1,1(u) = u - 1如果u 在[1,2)上, 而N_1,1(u) = 3 - u 如果 u 在[2,3)上。下图中，黑色和红色线分别是N_0,1(u)和  N_1,1(u)。注意N_0,1(u) (resp., N_1,1(u))在[0,1) 和[1,2) 上(resp., [1,2) 和 [2,3))是非零的。

　　

　　一旦获得N_0,1(u)和N_1,1(u)，可以计算N_0,2(u)。由定义得到下式:

　　

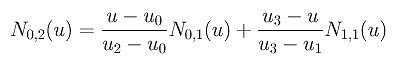
　　代入节点值得到

　　

　　注意 N_0,1(u) 在 [0,1)和[1,2)上非零而N_1,1(u) 在[1,2) 和 [2,3)上非零。因此，我们有三种情况要考虑：

（1） u 在 [0,1)上:
    这种情况，只有N_0,1(u)对N_0,2(u)的值有贡献。因此，N_0,1(u)是u, 得到

　　

（2）u 在[1,2)上:
    这种情况， N_0,1(u)和N_1,1(u)都对 N_0,2(u)有贡献。因此N_0,1(u) = 2 - u 且N_1,1(u) = u - 1 在[1,2)上,得到 

　　

　　【译注：上式中间的式子的第二项应为：0.5(3-u)(u-1)】

（3）u 在 [2,3)上:
    这种情况，只有N_1,1(u)对 N_0,2(u)有贡献。因此N_1,1(u) = 3 - u 在[2,3)上，得到,

　　

　  如果我们画出上述三种情况的曲线段，我们会看到两个相邻曲线段连接起来形成了在节点上的曲线。更确切地，第一种和第二种情况的曲线段在u = 1处连接起来，而第二种和第三种情况的曲线段在u = 2处连接起来。注意合成曲线是光滑的，但是如果节点向量包含多重节点通常就不是这样的。

　　

 

 

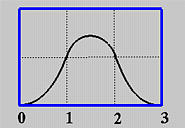
2. 两个重要的观察

　　因为 N_i,1(u) 是从 N_i,0(u) 和 N_i+1,0(u)计算的而 因为N_i,0(u)和N_i+1,0(u) 在区间[u_i, u_i+1)和[u_i+1, u_i+2)分别是非零的，N_i,1(u) 在这两个区间都是非零的。换句话说，N_i,1(u)在[u_i, u_i+2)上是非零的。相似地，因为 N_i,2(u) 依赖于N_i,1(u) 和N_i+1,1(u)且因为这两个基函数在[u_i, u_i+2)和[u_i+1, u_i+3)分别是非零的，N_i,2(u)在[u_i, u_i+3)上非零。总之，为确定基函数N_i,p(u), 的非零定义域，可以追溯到三角计算格式直到回到第一列。例如，假设我们想找到 N_1,3(u)的非零定义域。基于上述讨论，我们可从西北和西南方向追溯直到第一列为止，如下图中蓝色虚线所示。因此 N_1,3(u)在 [u₁, u₂), [u₂, u₃), [u₃, u₄) 和[u₄, u₅)上是非零的。或，相等地，它在[u₁, u₅)上非零。

　　

　　总之，我们有下列观察：

　　 基函数 N_i,p(u) 在[u_i, u_i+p+1)上非零。或，相等地，N_i,p(u) 在 p+1个节点区间[u_i, u_i+1), [u_i+1, u_i+2), ..., [u_i+p, u_i+p+1)上非零。

　　  接着，我们看相反的方向。给定一个节点区间[u_i, u_i+1),我们想知道哪个基函数会在计算中使用这个区间。我们可以以这个节点区间开始并画一个西北界限箭头和一个西南界限的箭头。所有封闭在楔形里的基函数使用 N_i,0(u)（为什么？）因此在该区间是非零的。因此，所有在[u_i, u_i+1)上非零的p 次基函数是这个楔形和包含所有N_i,p(u) 的列的交集。实际上，这一列和两个箭头形成一个等边三角形，而这一列是垂直边。 从 N_i,0(u) 数到 N_i,p(u) 有p+1列。因此，等边三角形的垂直边至多有p+1 项，即 N_i,p(u), N_i-1,p(u), N_i-2,p(u), ..., N_i-p+2,p(u), N_i-p+1,p(u) 和N_i-p,p(u)。

　　

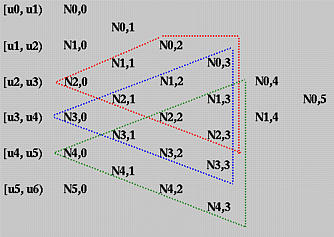
　　 让我们看上图。为了找到所有3次在 [u₄, u₅) 上非零的基函数，画出两个箭头和所有在垂直边的函数是我们想要的。这个例子，是N_1,3(u), N_2,3(u), N_3,3(u), 和N_4,3(u).用黄色三角表示。蓝色 (resp., 红色) 三角显示的是在[u₃, u₄) (resp., [u₂, u₃) )上非零的3次基函数。注意在[u₂, u₃)上只有3个3次基多项式。.

　　  总之，我们观察到下列特性：

　　 在任何一个节点区间 [u_i, u_i+1), 最多有 p+1个p 次基函数非零，即：N_i-p,p(u), N_i-p+1,p(u), N_i-p+2,p(u), ..., N_i-1,p(u) 和 N_i,p(u)。

3. 系数的意义是什么?

　　最后，让我们研究下N_i,p(u)定义中系数的意义。当计算 N_i,p(u) 时，它使用N_i,p-1(u)和N_i+1,p-1(u)。前者在 [u_i, u_i+p)上非零。如果u 是在这个半开区间，那么u - u_i 是u 和这个区间左端之间的距离，区间长度是u_i+p - u_i, ，而(u - u_i) / (u_i+p - u_i) 是上述距离的比且在0和1之间。见下图。第二项，N_i,p-1(u)，在[u_i+1, u_i+p+1)上非零。如果u 在该区间，那么u_i+p+1 - u 是 u 到该区间右端的距离，u_i+p+1 - u_i+1 是区间长度，而(u_i+p+1 - u) / (u_i+p+1 - u_i+1) 是这两个距离的比且值在0和1之间。因此, N_i,p(u) 是N_i,p-1(u) 和N_i+1,p-1(u)的线性组合，有两个系数，都在 u上是线性的，在0和1之间。

　　

---

B-spline Basis Functions:Important Properites

1. 这些基函数有如下性质，许多与贝塞尔基函数的相似

(1)N_i,p(u) 是一个在u 上的p 次多项式

(2)非负性

　 对所有的 i, p 和 u, N_i,p(u) 是非负的

(3)局部支撑（Local Support）

　　  N_i,p(u) 是在[u_i,u_i+p+1)上的非零多项式

(4)在任一区间 [u_i, u_i+1),最多有 p+1 个 p 次的基函数非零

　  即: N_i-p,p(u), N_i-p+1,p(u), N_i-p+2,p(u), ..., 和 N_i,p(u)

(5)单位分解（Partition of Unity）

　  所有非零的 p 次基函数在区间[ui, ui+1)上的和（sum）是 1， 上一条性质表明N_i-p,p(u), N_i-p+1,p(u), N_i-p+2,p(u), ..., 和 N_i,p(u) 在[u_i, u_i+1)上非零这条性质说明这些 p+1 个基函数的累加和1.

(6)如果节点数是 m+1, 基函数的次数是 p, 而p 次基函数的数目是n+1,，那么m = n + p + 1

　 这不难理解。 设 N_n,p(u) 是最后一个p 次基函数。它在 [u_n, u_n+p+1)上非零因为它是最后一个基函数， u_n+p+1 肯定是最后一个节点u_m。因此，我们有 u_n+p+1 = u_m 及 n + p + 1 = m. 总之，给定 m 和 p, 设 n = m - p - 1 则 p 次基函数是N_0,p(u), N_1,p(u), N_2,p(u), ..., 和 N_n,p(u).

(7)基函数 N_i,p(u) 是p 次多项式的复合曲线，连接点在[u_i, u_i+p+1 ) 上的节点处

　　例如  N_0,2(u), 其在 [0,3)上非零，是由定义在[0,1), [1,2) 和 [2,3)上的三个抛物线构建而成。它们在节点2 和3处连接在一起。.

(8)在一个有重复度k的节点处，基函数 N_i,p(u) 是 C^p-k 连续的

　　因此，增加重复度减小连续性的层次（level），增加次数增加连续性。上述2次基函数 N_0,2(u)在节点2 和 3处是 C¹连续的，因为它们是简单节点，重复读k=1。

2.多重节点的影响

 　多重节点对基函数的计算和一些“计算”性质有很重要的影响 。我们会看到其中两个：

（1）每个重复度 k 的节点减小最多k-1 基函数的非零定义域

　　考虑 N_i,p(u) 和 N_i+1,p(u). 前者在[u_i, u_i+p+1)上非零而后者在[u_i+1, u_i+p+2)上非零如果我们移动 u_i+p+2 到 u_i+p+1 以至于它们变为一个双重节点。那么， N_i,p(u) 仍然在 p+1节点区间上非零；但是，N_i+1,p(u) 非零的节点区间数目减小了一个因为区间[u_i+p+1,u_i+p+2) 消失了。

　　下图显示了5次基函数，其左端点节点和右端点节点有重复度6，而它们之间的所有节点数简单的（图（a））。图（b）是移动 u5 到 u6的结果。那些在u6 结束的基函数在更少的节点区间上非零。然后u4 再然后  u3 被移动到u6, 使得 u6 是重复度4的节点（图（c）和（d））。图（e）显示移动u2 到 u6 的结果，创建了一个重复度5的节点。

　　

（2）在每个重复度k的内部节点，非零基函数的数目最多p - k + 1, 其中 p 是基函数的次数

　　因为移动 u_i-1 到 u_i 会导致一个在u_i-1 结束非零的基函数移到u_i结束非零，这样使得在 u_i 上非零基函数的数目减小了一个。更准确地，u_i的重复度增加1会使得非零基函数的数目减小1.  因为在u_i 上最多有p+1 个基函数非零，那么在一个重复度k 的节点上最多有 (p + 1) - k = p - k + 1个非零基函数。在上述图中，因为节点u6 的重复度是1 (简单), 2, 3, 4 和 5, 在 u6 上的非零基函数数目是5, 4, 3, 2 和1.