[刷题] Leetcode算法 (2020-2-27)

1.最后一个单词的长度（很简单）

题目：

给定一个仅包含大小写字母和空格 ' ' 的字符串 s，返回其最后一个单词的长度。

如果字符串从左向右滚动显示，那么最后一个单词就是最后出现的单词。

如果不存在最后一个单词，请返回 0 。

说明：一个单词是指仅由字母组成、不包含任何空格的 最大子字符串。

示例：

输入: "Hello World"
输出: 5

代码：

class Solution:
    def lengthOfLastWord(self, s: str) -> int:
        # 如果s为空即""，直接返回0
        if not s:
            return 0
        # 按空格分隔成多个列表（前后空格会被自动剔除）
        s_list = s.split()
        # 如果s_list为空列表[],则返回0。在s = "   "这种情况下，s_list会是空列表
        if not s_list:
            return 0
        # 返回最后一个单词的长度
        return len(s_list[-1])

这个题非常简单。

2.加一（很简单）

题目：

给定一个由整数组成的非空数组所表示的非负整数，在该数的基础上加一。

最高位数字存放在数组的首位， 数组中每个元素只存储单个数字。

你可以假设除了整数 0 之外，这个整数不会以零开头。

示例：

输入: [1,2,3]
输出: [1,2,4]
解释: 输入数组表示数字 123。

输入: [4,3,2,1]
输出: [4,3,2,2]
解释: 输入数组表示数字 4321。

代码1：

class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        # 从个位数往前循环
        for i in range(len(digits)-1,-1,-1):
            # 如果加1小于10，则加1直接返回即可
            if digits[i] + 1 < 10:
                digits[i] += 1
                break
            # 如果加1等于10，说明进位
            else:
                # 该位为0，继续下一次循环（前一位继续+1）
                digits[i] = 0
                # 特殊情况，如果已经是最高位，则需要在index=0的位置加一位
                if i == 0:
                    digits.insert(0,1)
        return digits

普通进位做法。从各位开始，每一位加1是否进位，进位则循环前面一位数，直到不进位为止。

代码2：

class Solution:
    def plusOne(self, digits: List[int]) -> List[int]:
        # 将列表中的数字全部转换为字符
        s = [str(i) for i in digits]
        # 字符列表-->字符串-->数字-->加1-->字符串-->字符列表
        return [int(i) for i in list(str(int(''.join(s)) + 1))]

利用python语言的便利性来做。

3.二进制求和

题目：

给定两个二进制字符串，返回他们的和（用二进制表示）。

输入为非空字符串且只包含数字 1 和 0。

示例：

输入: a = "11", b = "1"
输出: "100"

输入: a = "1010", b = "1011"
输出: "10101"

代码：

class Solution:
    def addBinary(self, a: str, b: str) -> str:
        # 将a和b都转换为十进制数字
        a, b = eval('0b' + a), eval('0b' + b)
        # ab的和-->二进制-->字符串-->去掉'ob'
        return str(bin(a+b))[2:]

4.X的平方根

题目：

实现 int sqrt(int x) 函数。

计算并返回 x 的平方根，其中 x 是非负整数。

由于返回类型是整数，结果只保留整数的部分，小数部分将被舍去。

示例：

输入: 8
输出: 2
说明: 8 的平方根是 2.82842..., 
     由于返回类型是整数，小数部分将被舍去。

代码1：

class Solution:
    def mySqrt(self, x: int) -> int:
        i = 0
        while True:
            if i ** 2 > x:
                return i-1
            elif i ** 2 == x:
                return i
            i += 1

暴力法，从0开始一个一个试，当平方大于x的时候，i-1就是结果。时间复杂度O(n)。

代码2：

class Solution:
    def mySqrt(self, x: int) -> int:
        if x == 0:
            return 0
        left = 1
        right = x // 2
        # 当最后找到值得时候，left会等于right
        while left < right:
            # 注意：这里一定取右中位数，如果取左中位数，代码可能会进入死循环
            mid = (left + right + 1) >> 1
            square = mid * mid
            
            if square > x:
                right = mid - 1
            else:
                left = mid
        # 因为一定存在，因此无需后处理
        return left

二分法，时间复杂度O(logn)。

5.爬楼梯（青蛙跳楼梯）

题目：

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1.  1 阶 + 1 阶 + 1 阶
2.  1 阶 + 2 阶
3.  2 阶 + 1 阶

代码1：

class Solution:
    def climbStairs(self, n: int) -> int:
        # 结束条件
        if n == 1:
            return 1
        if n == 2:
            return 2
        # 递归规律，n梯的爬法 = n-1的爬法数 + n-2的爬法数
        return self.climbStairs(n-2)+ self.climbStairs(n-1)

递归解法，结束条件很简单，重要是找到规律。

代码2：（DP很不错）

class Solution:
    def climbStairs(self, n: int) -> int:
        # 前三个元素为n=0,n=2,n=2时的爬法数
        climb = [0,1,2]
        # 从3开始循环[3,n]
        for i in range(3,n+1):
            # 在数据对应的index记录index个台阶的爬法数，同样利用的递归中找到的规律
            climb.append(climb[-1] + climb[-2])
        return climb[n]

DP解法，和递归的原理一样，只是使用了一个列表来记录每次的计算结果。与递归的不同就是不用开辟非常多的栈（太深要导致程序崩）。

6.杨辉三角

题目：

给定一个非负整数 numRows，生成杨辉三角的前 numRows 行。

 

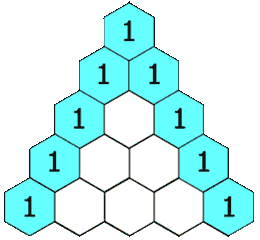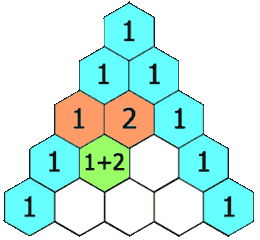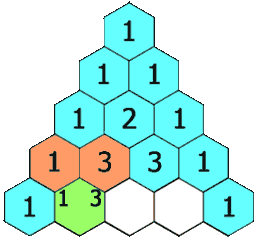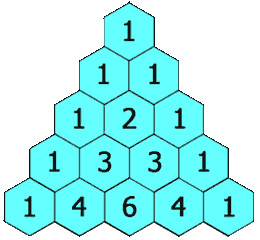
在杨辉三角中，每个数是它左上方和右上方的数的和。

示例：

输入: 5
输出:
[
     [1],
    [1,1],
   [1,2,1],
  [1,3,3,1],
 [1,4,6,4,1]
]

代码1：

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        res = []
        if not numRows:
            return res
        res.append([1])
        if numRows == 1:
            return res
        res.append([1,1])
        if numRows == 2:
            return res

        # 上一行的元素，两两相加，放入一个列表。然后前后各添一个1，就得到下一行的列表
        def createNext(li):
            temp = []
            for i in range(0,len(li)-1):
                temp.append(li[i]+li[i+1])
            temp.insert(0,1)
            temp.append(1)
            return temp
        
        # 迭代的计算每一行，全部append到res中
        init = res[-1]
        for i in range(3,numRows+1):
            nex = createNext(init)
            res.append(nex)
            init = nex
        return res

杨辉三角的规律就是从第3行起，除边缘两个元素是1，中间的元素都是前一行元素两两相加的和。所以思想就是由上一行生成下一行的元素。上述代码是比较low的写法。

代码2：

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
        # 如果numRows=0，直接返回空列表
        if numRows == 0: return []
        # 初始res为numRows=1时的结果
        res = [[1]]
        # 当len(res)<numRows时，表示后面还需要继续算
        while len(res) < numRows:
            # 计算下一行列表nex。这里比较巧妙，观察到规律 [1,3,3,1] = [0]+[1,2,1] 对应元素加 [1,2,1]+[0],利用zip()可以做到对应元素求和。
            nex = [a+b for a, b in zip([0]+res[-1], res[-1]+[0])]
            res.append(nex)      
        return res

以上是比较巧妙的写法，找出后一行和前一行的核心规律。 [1,3,3,1] = [0]+[1,2,1] 和 [1,2,1]+[0] 对应元素的和。然后利用zip来协助求解对应元素的和。

总结：

# 这种看似有规律的题，一定要多发现不同的规律。有些规律很明显，但不一定是最好的规律。
# 一旦发现了最方便的规律。代码会更简洁易懂

 

##