OpenCV笔记（3）(Canny边缘检测、高斯金字塔、拉普拉斯金字塔、图像轮廓、模板匹配)
一、Canny边缘检测
Canny边缘检测是一系列方法综合的结果。其中主要包含以下步骤：
1.使用高斯滤波器，平滑图像，滤除噪声。
2.计算图像中每个像素点的梯度强度和方向。
3.应用非极大值抑制（NMS：Non-Maximum Suppression），以消除边缘检测带来的杂散相应。
4.应用双阈值（Double-Threshold）检测来确定真实和潜在的边缘。
5.通过抑制孤立的弱边缘最终完成边缘检测。
1.高斯滤波器
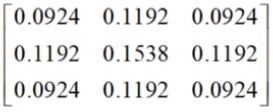
平滑图像。
2.计算梯度和方向
使用X和Y方向的Sobel算子来分别计算XY方向梯度：
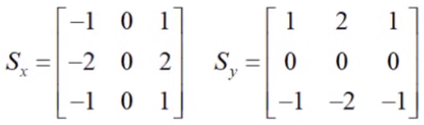
每个点的梯度强度有XY方向的梯度计算出来：
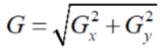
计算每个点梯度的方向：
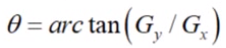
3.使用NMS
有两种方法，第一种方法（插值法，比较复杂）：
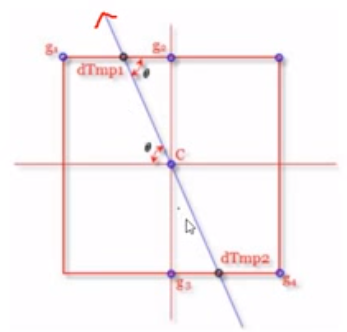
通过计算出的梯度方向，找到与周边临近点的边的交点，然后使用权重计算交点的值，假设g1和g2之间的交点（左上的黑点）处于6/4的位置，那么他的值为M = g1*(1-0.6)+g2*(0.4)。
当算出左上的黑点和右下的黑点值后，用这两个点与C的值进行比较，如果都小于C，则C归为边界。如果有一个比C大，则丢弃C，这就叫抑制。
第二种方法（指定8个方向，不用插值，简化版）：
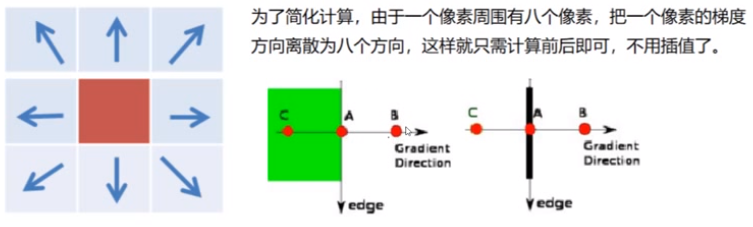4.双阈值检测
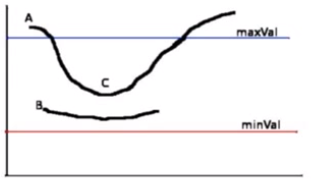在NMS的基础上，判断一个边界点的梯度强度：
(1) 如果值大于maxVal，则处理为边界
(2) 如果值minVal<梯度值<maxVal，再检查是否挨着其他边界点，如果旁边没有边界点，则丢弃，如果连着确定的边界点，则也认为其为边界点。
(3) 梯度值<minVal，舍弃。
通过以上步骤，完成Canny边缘检测。调用Canny API如下：
# 使用Canny边界检测 def use_canny(image): # 后面两个参数代表双阈值检测的minVal和maxVal img1 = cv.Canny(image, 50, 100) cv.imshow('img1', img1) # 这里使用更大的minVal和maxVal,细节边界变少了 img2 = cv.Canny(image, 170, 250) cv.imshow('img2', img2)
二、高斯金字塔
图像金字塔：Image pyramid
如图中所示，从0到3是一个下采样过程（指图片越来越小的方向），从3到0是一个上采样过程（将图片变大的过程），一次下采样加一次上采样不等于原图像，因为会损失一些细节信息。
# 下采样（图片变小4倍,即hw各缩小一倍） def down_sample(image): down = cv.pyrDown(image) cv.imshow('down', down) # 上采样（图片变大4倍,即hw各变大一倍） def up_sample(image): up = cv.pyrUp(image) cv.imshow('up', up)
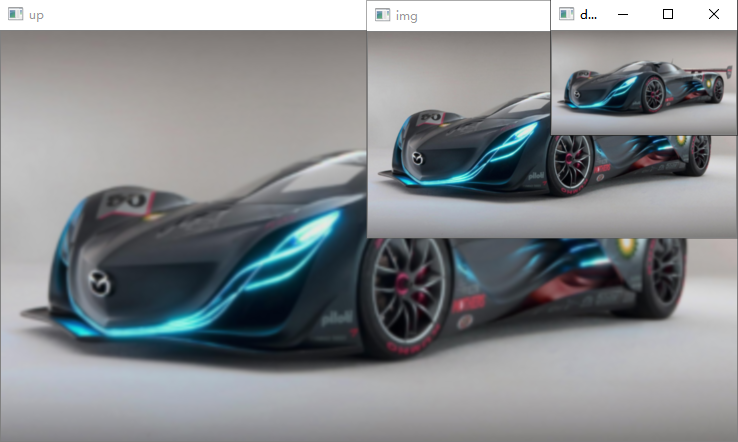
上采样+下采样=原图？？
如下图所示，很明显，经上采样后下采样得到的图片（右图）和原图（左图）相比，更加模糊，说明丢失了一些信息。
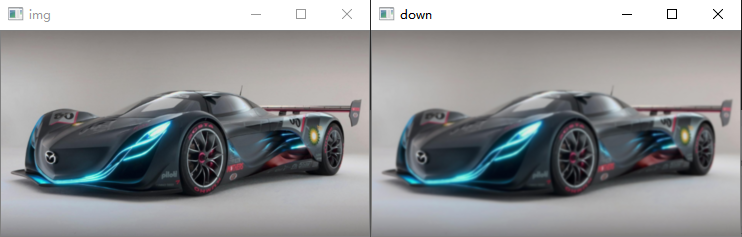
先经上采样，后经下采样的图像结果如下（大小未发生变化）：
原始图像: (205, 368, 3)
上采样后: (410, 736, 3)
上采样+下采样后: (205, 368, 3)
下采样+上采样=原图？？
如下图所示，非常明显，经下采样后上采样得到的图片和原图相比，模糊很严重，说明这种情况下丢失信息更加严重。
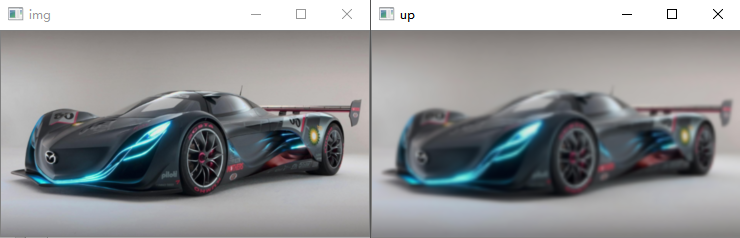
当h或w为单数时，下采样后其将变为单数，如下结果所示：
原始图像: (205, 368, 3) 下采样后: (103, 184, 3) 下采样+上采样后: (206, 368, 3)
原始图像和经下采样上采样后的图像大小发生了变化。
三、拉普拉斯金字塔
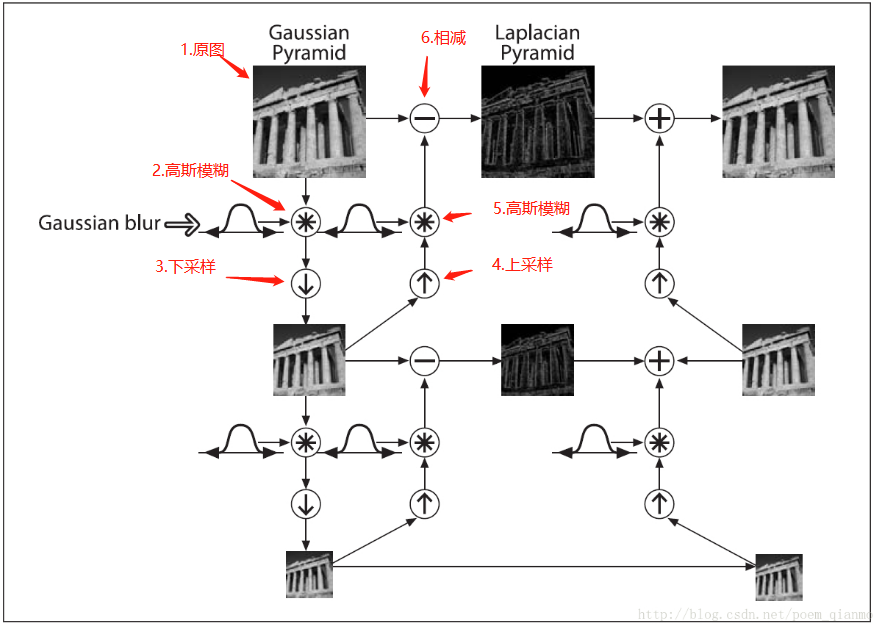
拉普拉斯金字塔的整个计算过程如上图所示：
1.左上角的图片为原始图片
2.对原始图像进行高斯平滑
3.执行一次下采样，图像变为原来的1/4
4.执行一次上采样，图像变为原图的大小
5.再次执行高斯模糊
6.用原图像减去高斯模糊后的图像，得到拉普拉斯图像
上述过程是某一层拉普拉斯金字塔的计算过程，其他层同样按这个过程计算。
def lap_pyr(image): img = image.copy() # 处理h或w为奇数的情况，如果为奇数，丢弃最后一行或列 h, w = image.shape[0:2] if h % 2 != 0: img = img[0:h - 1, :, :] if w % 2 != 0: img = img[:, 0:w - 1, :] gaus = cv.GaussianBlur(img, (3, 3), 0) down = cv.pyrDown(gaus) up = cv.pyrUp(down) gaus_up = cv.GaussianBlur(up, (3, 3), 0) diff = gaus - gaus_up # 返回下一层的原始图像（即高斯模糊后下采样得到的图像），以及本层拉普拉斯图像 return down,diff
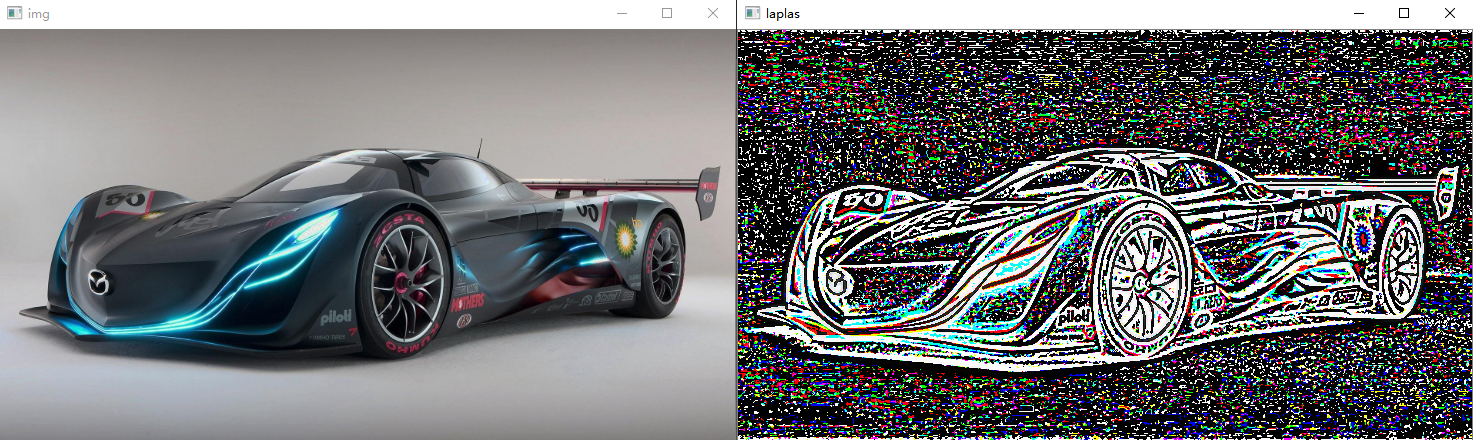
得到的图像如上图，但噪声很大。
四、图像轮廓
# 要找一个图中的轮廓，首先要将图片转换为二值图像 def find_contour(image): # 首先将图片转换为灰度图 gray = cv.cvtColor(image, cv.COLOR_RGB2GRAY) # 将灰度图转换为二值图像 ret, thresh = cv.threshold(gray, 127, 255, cv.THRESH_BINARY) cv.imshow('二值图像', thresh) # 在二值图像中寻找轮廓，返回的contours中含有多个轮廓 contours, hierarchy = cv.findContours(thresh, cv.RETR_TREE, cv.CHAIN_APPROX_NONE) # 复制一份原图像 draw_img = image.copy() # 在复制的图上画出轮廓，颜色为(0,0,255)红色，-1表示画出全部轮廓，指定0则表示只画第一个轮廓，
# 最后的2表示画线的粗细 res = cv.drawContours(draw_img, contours, -1, (0, 0, 255), 2) cv.imshow('轮廓图', res)
图像结果，左边为二值图像，右边为在原图的拷贝上画出的轮廓。
上述代码中关键函数为cv.findContours(img,mode,method)：
img：原图像的二值图像，见代码中的转换
mode：轮廓检索模式，主要有一下几种，最常用的是RETR_TREE
RETR_EXTERNAL：只检索最外面的轮廓；
RETR_LIST：检索所有的轮廓，并将其保存到一条链表当中；
RETR_CCOMP：检索所有的轮廓，并将他们组织为两层，顶层是各部分的外部边界，第二层是空洞的边界
RETR_TREE：检索所有的轮廓，并重构嵌套轮廓的整个层次。
method：轮廓逼近方法，常用的有一下两种（还有其他不常用的）
CHAIN_APPROX_NONE：以Freeman链码的方式输出轮廓，所有其他方法输出多边形
CHAIN_APPROX_SIMPLE：压缩水平的、垂直的和斜的部分，也就是，函数只保留他们的终点部分。如下图所示，锁边为NONE，右边为SIMPLE。
计算轮廓包含的面积，周长等：
# 计算轮廓包含的面积 print(cv.contourArea(contours[0])) print(cv.contourArea(contours[1])) # 计算第一个轮廓的周长，True表示闭合的 print(cv.arcLength(contours[0], True))
轮廓近似：
draw_img2 = image.copy() # 用周长的0.3倍作为阈值，对轮廓做近似处理，这里以第189个轮廓为例 epsilon = 0.03 * cv.arcLength(contours[188], True) approx = cv.approxPolyDP(contours[188], epsilon, True) res2 = cv.drawContours(draw_img2, [approx], -1, (255, 0, 0), 2) cv.imshow('res2', res2)draw_img2 = image.copy() # 用周长的0.3倍作为阈值，对轮廓做近似处理，这里以第189个轮廓为例 epsilon = 0.03 * cv.arcLength(contours[188], True) approx = cv.approxPolyDP(contours[188], epsilon, True) res2 = cv.drawContours(draw_img2, [approx], -1, (255, 0, 0), 2) cv.imshow('res2', res2)
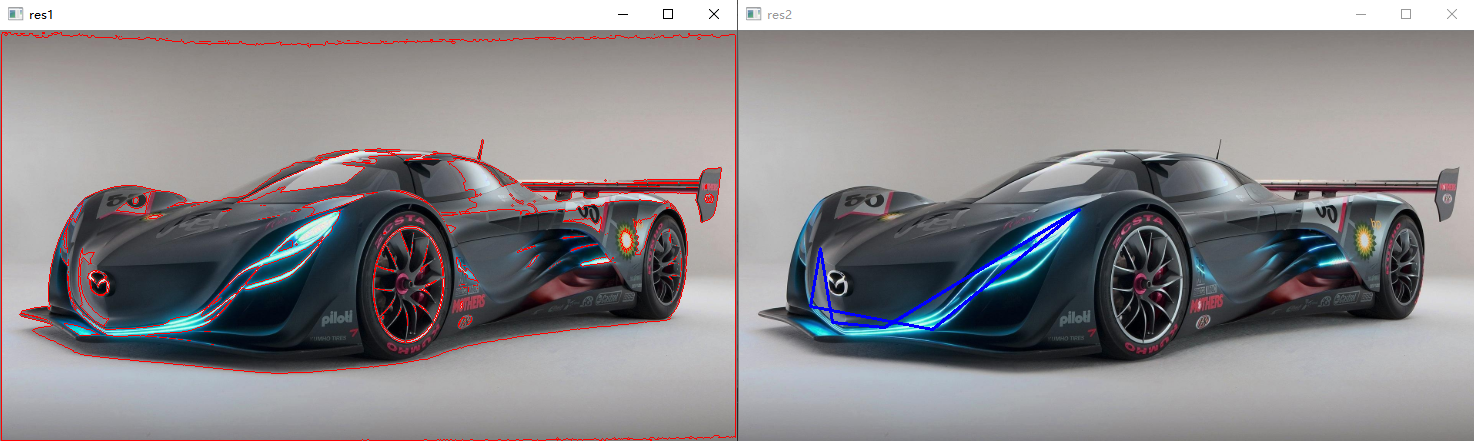
对所有轮廓都做近似处理：
# 将contours中的左右轮廓都做近似处理 new_contours = [] for i in contours: eps = 0.01 * cv.arcLength(i,True) approx = cv.approxPolyDP(i,eps,True) new_contours.append(approx) draw_img2 = image.copy() res2 = cv.drawContours(draw_img2, new_contours, -1, (255, 0, 0), 2) cv.imshow('res2', res2)
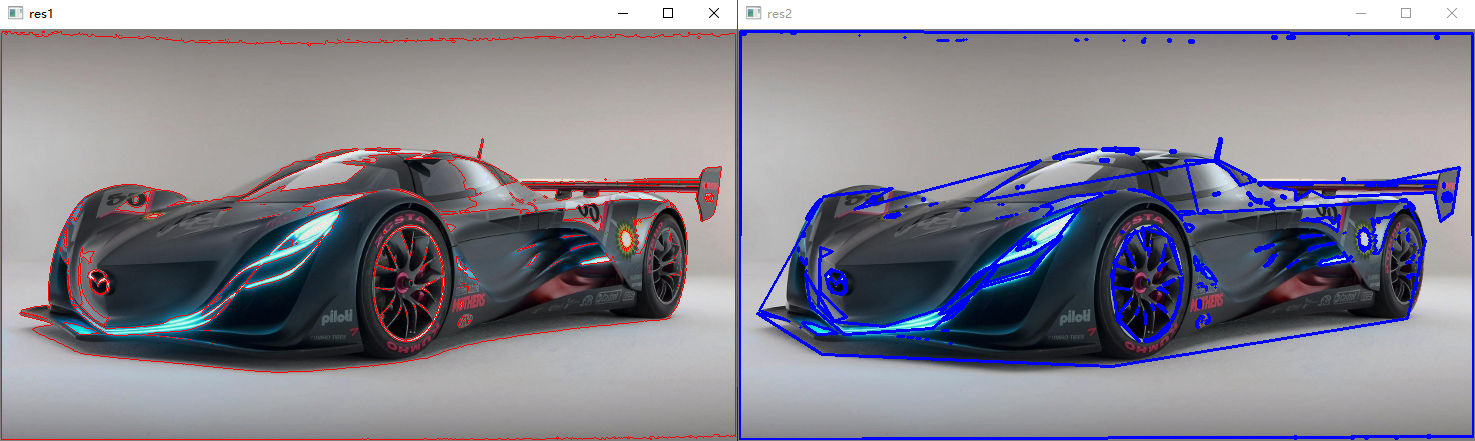
外接矩形：
x, y, w, h = cv.boundingRect(contours[188]) rect = cv.rectangle(draw_img2, (x, y), (x + w, y + h), (0, 255, 0), 2) cv.imshow('rect', rect)
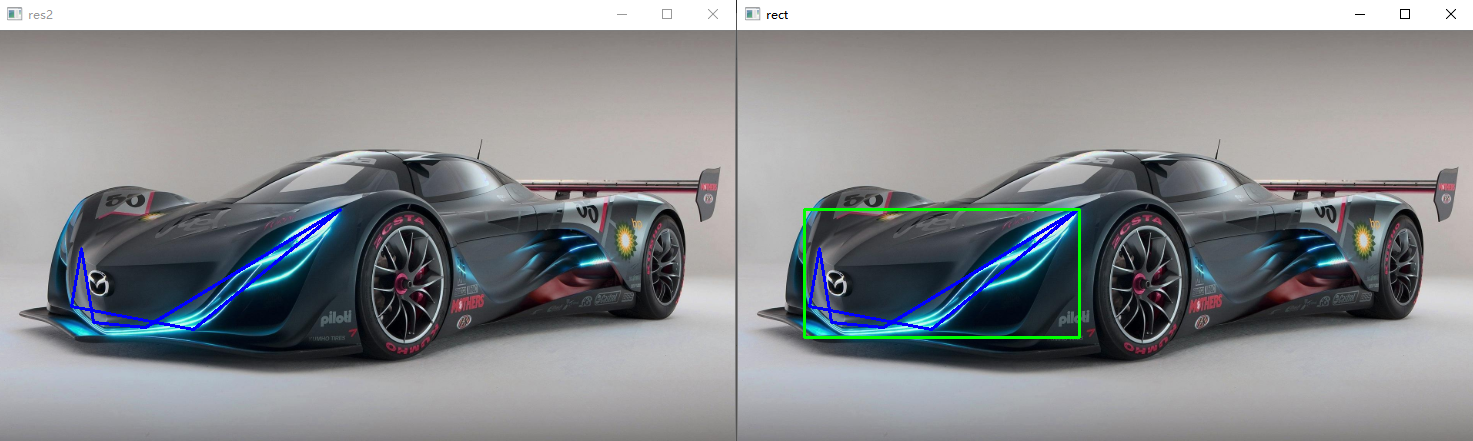
最小矩形：
可以通过轮廓来获取其最小矩形，用于定位车牌等很有用（车牌不是正的时候）
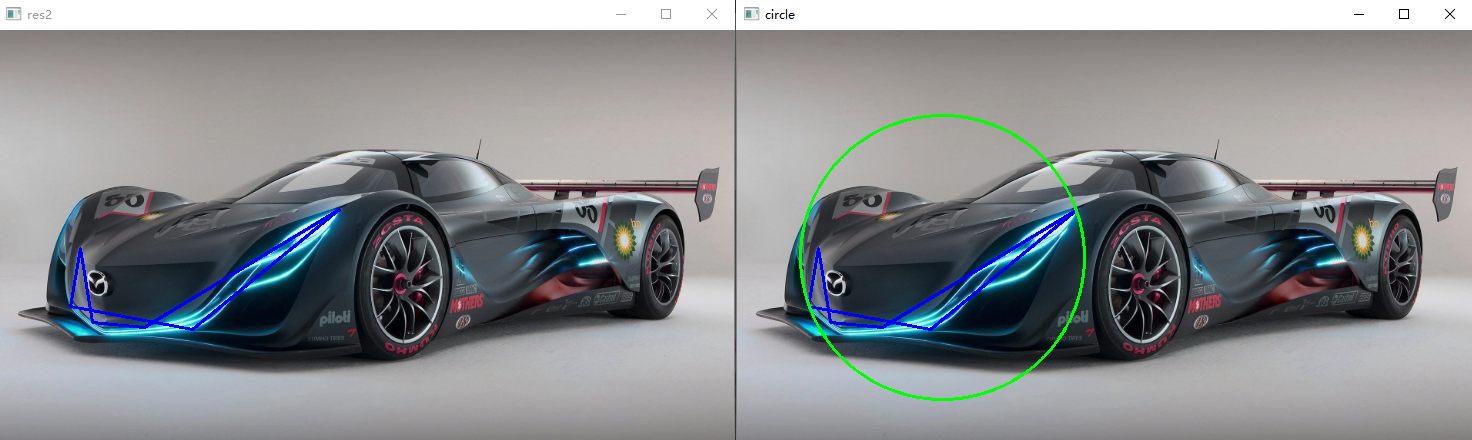
# 获取最小矩形 res = cv.minAreaRect(contours[188]) # box中保存的是由四个顶点坐标组成的二维数组，通过4个顶点，我们可以将车牌抠出来 box = cv.boxPoints(res) box = np.int32(box) # 用polylines将矩形画出来 box = box.reshape(-1, 1, 2) cv.polylines(draw_img2, [box], True, (0, 0, 255), 2)
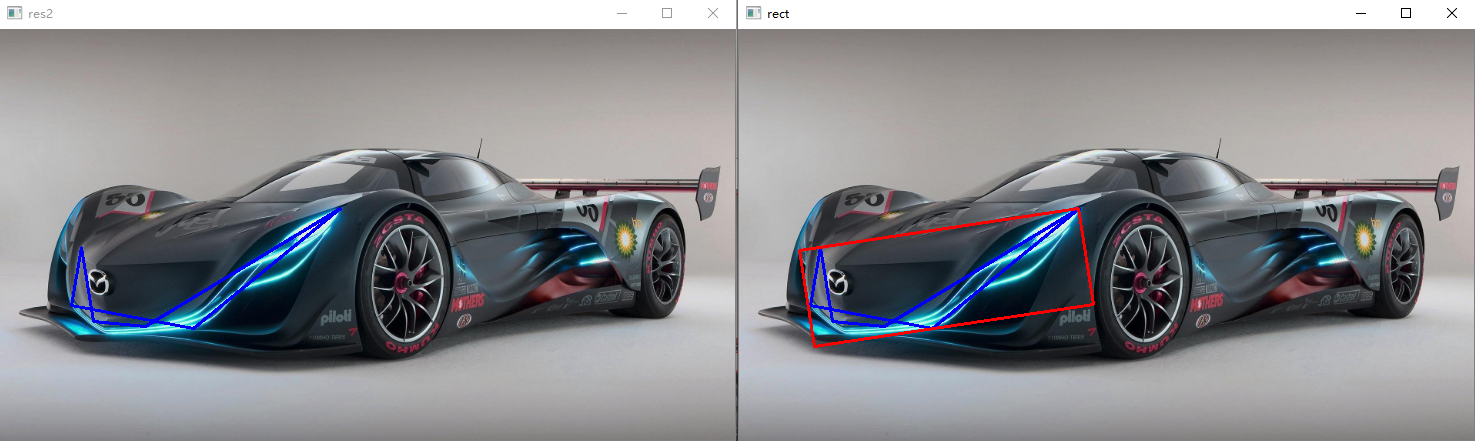
外接圆：
# 获取外接圆 (x, y), r = cv.minEnclosingCircle(contours[188]) center = (int(x), int(y)) radius = int(r) circle = cv.circle(draw_img2, center, radius, (0, 255, 0), 2) cv.imshow('circle', circle)
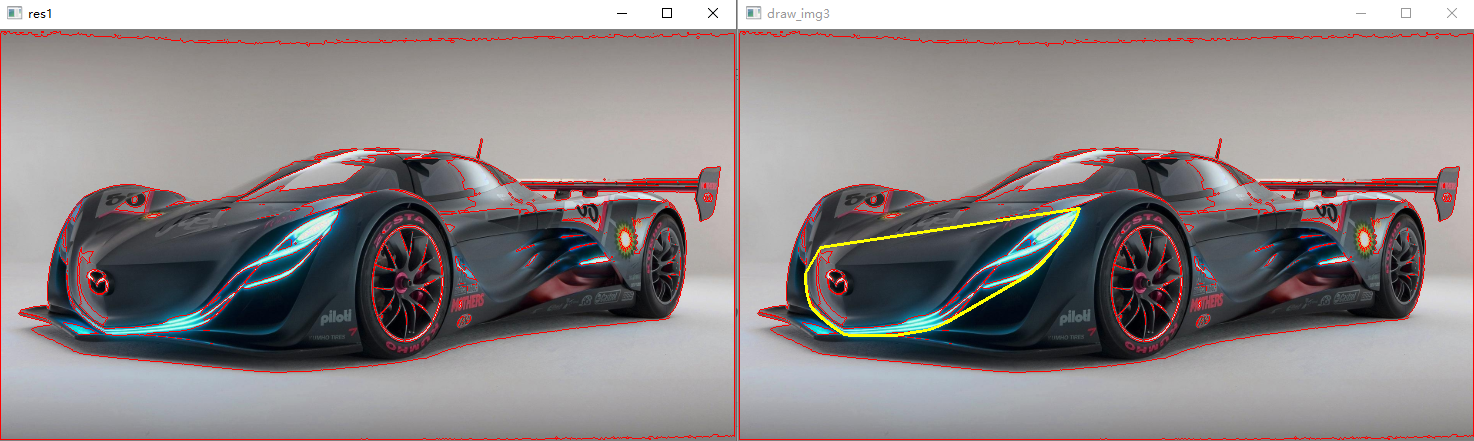
凸包：
convex Hull，获取轮廓的外接凸包，获得N个坐标，仍然用line画出。
res = cv.convexHull(contours[188]) length = len(res) for i in range(length): cv.line(draw_img3, tuple(res[i][0]), tuple(res[(i + 1) % length][0]), (0, 255, 255), 2) cv.imshow('draw_img3', draw_img3)
五、模板匹配
例如，我们要在一张图中匹配其中的一部分图像，并找到其具体坐标：
# 模板匹配 def template_match(src, temp): # 转换为灰度图像可以减少计算量 src = cv.cvtColor(src, cv.COLOR_RGB2GRAY) temp = cv.cvtColor(temp, cv.COLOR_RGB2GRAY) # 获取temp的h和w h, w = temp.shape[0:2] # 将原图和局部图输入，计算出一个差异矩阵res res = cv.matchTemplate(src, temp, cv.TM_SQDIFF) # 得到这个diff矩阵中的最小值、最大值以及所在位置,都是tuple min_val, max_val, min_loc, max_loc = cv.minMaxLoc(res) # 我们使用的是平方误差，值需要关心最小值所在位置 img = src.copy() # 用白色将对应的框画出来 rect = cv.rectangle(img, min_loc, (min_loc[0] + h, min_loc[1] + w), 255, 2) cv.imshow('rect', rect)
其中求diff矩阵的函数cv.matchTemplate(img,temp,cv.TM_SQDIFF)的第三个参数有以下选择：
1.TM_SQDIFF: 计算平方误差，值越小，越相关
2.TM_CCORR: 计算相关性，计算出来的值越大，越相关
3.TM_CCOFFF: 计算相关系数，计算出来的值越大，越相关
4.TM_SQDIFF_NORMED: 计算归一化的平方误差，越接近0越相关
5.TM_CCPRR_NORMED: 计算归一化的相关性，越接近1，越相关
6.TM_CCOFFF_NORMED: 计算归一化的相关系数，越接近1，越相关
