机器学习-4 神经网络
一、概念
多层向前神经网络(Multilayer Feed-Forward Neural Network)。
核心算法 ： Backpropagation，BP算法
由以下部分组成：
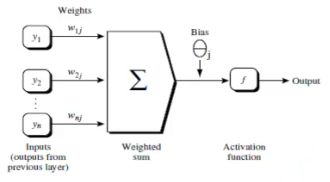
输入层(Input layers)：用于训练集（测试集）实例特征向量的传入。
隐藏层(Hidden layers)：层数是任意的，每一层的输出是一下层的输入。
输出层(Output layers)：输出最终结果（类别）。
单元（Units）：每一层由多个单元组成。
权重（weight）：层与层之间的每一个链接，都有一个权重，记为wij。
偏向（bias）：每一个node有一个偏向值（bias），与权重配合来计算每个节点的输出，记为θj。
层数（layers）：神经网络的层数一般不包含输入层，所以上图的网络为2层。
作为多层向前神经网络，理论上，如果有足够多的隐藏层和足够大的训练集，可以模拟出任何方程。
二、使用神经网络
在使用神经网络前，需满足下面两个要求：
1.使用神经网络训练数据之前，必须确定神经网络的层数，以及每一层单元的个数。
2.特征向量在被传入输入层时要先标准化（normalize）到0-1之间（为了加速学习过程）。
3.离散型变量可以被编码成一个输入单元对应一个特征值可能赋的值。
比如：特征值A可能取三个值(a0,a1,a2)，可以使用3个输入单元来代表A，当A=a0时，那么代表a0的单元就取1，其他取0，即(1,0,0)，当A=a1时，即(0,1,0)。
神经网络可以处理一下两种问题：
1.分类(classification)问题。
2.回归(regression)问题。
神经网络主要解决分类问题，对于分类问题，如果最终结果分为2类，则可以用一个输出单元来表示（0和1分别代表2类）。
如果多余2类，每一个类别用一个输出单元表示。所以输出层的单元数量通常等于类别的数量。
隐藏层层数：
没有明确的规则来设计最好有多少隐藏层，需根据实验测试和误差以及准确度来实验并改进。
三、交叉验证方法
Cross-validation
传统的验证方法是将整个数据集分为两份：其中一份用作训练集，另一份用作测试集。
这样虽然简单，但是可能会因为偶然性导致测试结果不准确。
交叉验证方法：将数据集分为多份（例如10份）。第一次使用第一份作为测试集，剩下九份作为训练集。第二次使用第二份作为测试集，剩下九份作为训练集。通过10次训练与测试，能够更合理的评估神经网络结构的有效性。
四、神经网络训练过程
输入：训练数据集(data set)，学习率(learning rate，关系训练的收敛速度，和梯度下降算法相关)，一个多层向前神经网络。
输出：一个训练好的神经网络(A trained neural network)。
对于每一个训练实例X，执行以下步骤：
- 由输入层向前传递：
1.对于第一个隐藏层的节点 j，输入值的计算公式为：
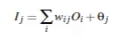
2.将输入值经过一个激励方程(Activation function)转化为一个0-1的输出值
一般来说，激励方程使用以下sigmoid函数（另一个常用的是tanh(x)函数）：
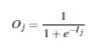
- 反向转播：
1.当每个输出层节点的输出计算出来后，计算与当前实例的分类之间的误差：
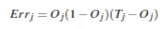
其中Oj(1-Oj)为sigmoid函数的导数，具体推导过程参照学习资料的1.如果激励函数使用的是tanh，则导数为1-(Oj)2。
2.对于隐藏层，同样要计算输出误差：
隐藏层某节点的输出误差与它后面链接的各输出层节点或隐藏层节点的输出误差及权重有关。
3.将所有隐藏层和输出层的误差都算出来以后，需要更新权重：
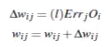
其中的(l)表示前面提到的学习率，用于控制梯度下降的速度（步长），取0-1之间的值，值越大训练越快，但可能会导致步伐太大，跨过曲面最低点。
4.同样更新偏向值（bias）：
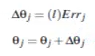
终止条件：
- 权重的更新低于某个阈值
- 预测的错误率低于某个阈值
- 达到预设一定的循环次数
五、实例训练过程（手工计算）
1.网络结构：
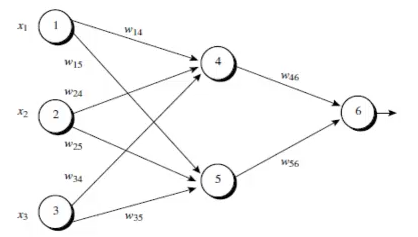
2.训练第一个实例（1,0,1）之前，随机产生所有的权重(-0.5-0.5之间)和偏向值(-0.5-0.5之间)。
3.计算正向转播中，隐藏层和输出层所有节点的值。
4.假设训练实例标签是1，即Tj=1。按一下公式计算输出层节点的误差。
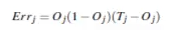
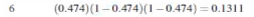
5.计算隐藏层的误差。
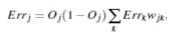
6.更新权重。
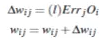
7.更新偏向。
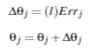
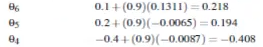
偏向可以认为是输入始终为1的wij。
8.训练结束。
