机器学习-2 决策树

一、例子：

　　用年龄、收入、是否学生、信用度高低来判断是否购买电脑为例子：

　　

 

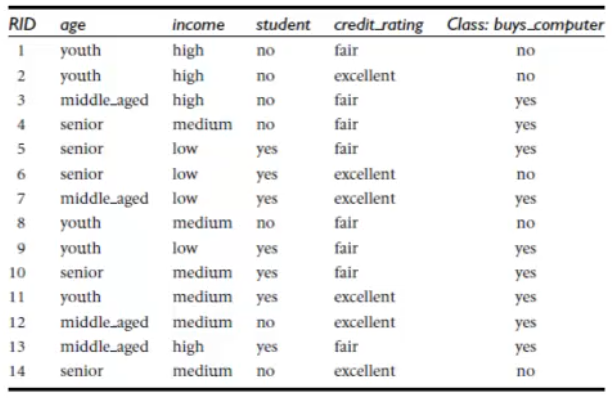
二、根节点的选择

　　信息：如果待分类的事物可能划分在多个类之中，则符号x_i的信息定义为：

　　　　　　　　

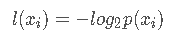
　　上例中，买电脑的概率为9/14，那么yes的信息为：

　　　　　　　　

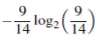
　　同理，no的信息为：

　　　　　　　　

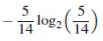
　　信息熵：即信息期望值。公式如下：

　　　　　　　　

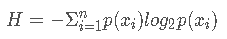
　　即：

 　　　　　　　　

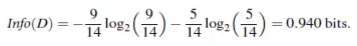
　　在决策树ID3算法中，选择使用信息获取量（Information Gain）作为节点选择的依据，也叫类与特征的互信息（D与A的互信息）：

　　　　　　　　　

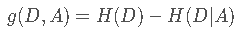
　　在上面我们已经求得了H(D)(即上面的Info(D))，H(D|A)代表的是在A的情况下D的信息熵。

　　　　　　　　　　

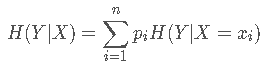
　　例如例子中的H(buy computer | age)，计算如下：

　　　　　　　　

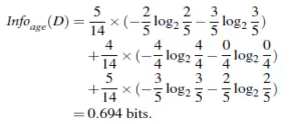
　　所以，g(buy computer, age) = 0.940-0.694 = 0.246 bits

 

　　类似的，可以求得income,student,credit_rating的信息获取量分别是：

　　g(buy computer, income) = 0.029 bits

　　g(buy computer, student) = 0.151 bits

　　g(buy computer, credit_rating) = 0.048 bits

　　去其中最大值作为根节点，即age作为分类根节点。

 

三、计算后续节点

　　在选择好根节点后，我们将训练集按age划分，并将age属性从训练集中剔除，得到以下三个列表：

　　

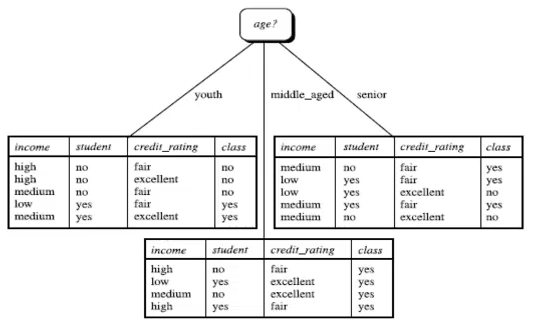
　　我们按选择根节点时计算信息获取量的方法，作用于每个分支的子数据集。从而可以选择第二层的分类节点。

 

四、处理连续值

　　当数据中有连续型数据，例如age数据并不是youth、middle_aged、senior，而是具体的岁数。

　　我们需要将连续型数据进行预处理，将其进行阈值划分，例如1-25为youth，26-50为middle_aged，51-100为senior。

 

五、划分结束条件

• 给定节点的所有样本属于同一类。例如age划分后的middle_aged。
• 没有剩余属性可以用来进一步划分样本。在此情况下，使用多数表决的方法。

　　如何避免overfitting：

　　　　当决策树层数过多时，可能因为划分太细而导致过拟合（overfitting），这是可以采取修建枝叶的方法来避免。

　　　　1.先剪枝：在生成决策树的过程中，当类别占比达到一定程度时不再往下细分。

　　　　2.后剪枝：在决策树完全创建后，再根据一些规则来对枝叶进行修剪。 

 

六、其他的决策树算法

　　C4.5算法。

　　CART算法：Classification and Regression Trees。

　　共同点：都是贪心算法，自上而下(Top-down approach)。

　　区别：属性选择度量方法不同，例如C4.5采用gain ratio，CART采用gini index，ID3采用Information Gain。

 

七、决策树的优点和缺点

　　优点：直观，便于理解，小规模数据集有效。

　　缺点：处理连续变量不是很好，类别较多时，错误增加的比较快，可规模性一般。