堆排序和选择排序
选择排序的执行过程为每次循环遍历数组找出最小(或最大)的数,将其放在数组的有序数列的最后面,每次第i次遍历查找要执行N-i个单位时间,然后要执行N次,故时间复杂度为O(N^2),很简单,比较适合较小的数列的排序。
选择排序的代码selection_sort.cpp会在下面的完整代码中呈现。
而堆排序是对于选择排序的优化排序,它利用率了最大(最小)堆顶的数最大(最小)的性质,使得找到一个数组找到最大(最小)的元素的操作不需要像选择排序一样消耗N-i的时间。其时间复杂度为O(nlogn),空间复杂度为O(1)。
在介绍堆排序的执行过程前,先要了解几个公式:
对于一个根节点 i,其左子树为 2*i+1,其右子树为 2*i+2 ,而最后一个有子树的根节点 a 的位置小于等于 N/2,N是待排序数组的长度。
本文中有关堆排序的介绍图片都是转自下面的作者的博客:
作者: dreamcatcher-cx
出处: <http://www.cnblogs.com/chengxiao/>
其执行过程如下:
1.先建立最大(最小)堆(build_heap)
1.1 将数组导入一颗完全二叉树;
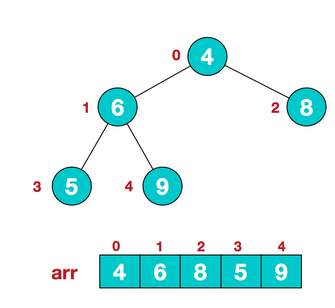
1.2 从倒数第一个有子树的根节点开始建立堆(heapify)(操作就是通过比较和变换使得根节点的大小大于(小于)子树的大小。),然后对前面一个根节点做同样的循环操作,直到堆顶也操作结束,则完成建立整个堆。
在heapify的过程中,我们要在改变了一个子树跟根节点位置后,再向下调整其子树的子树和其子树的位置,直至最后一个子树。
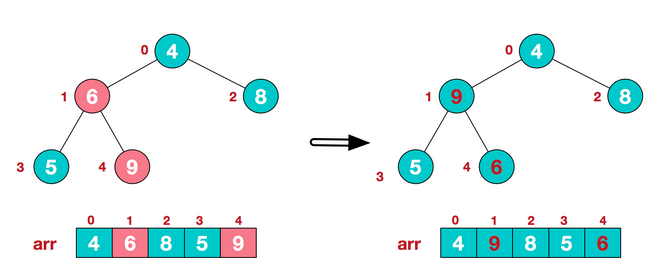
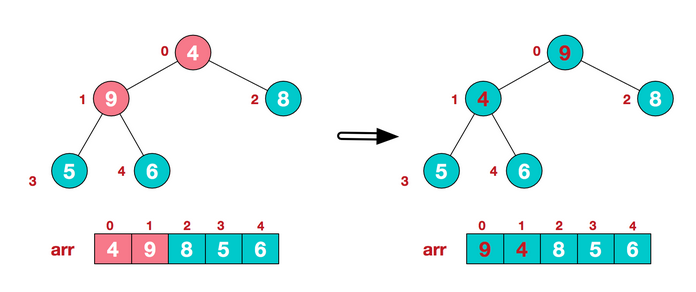
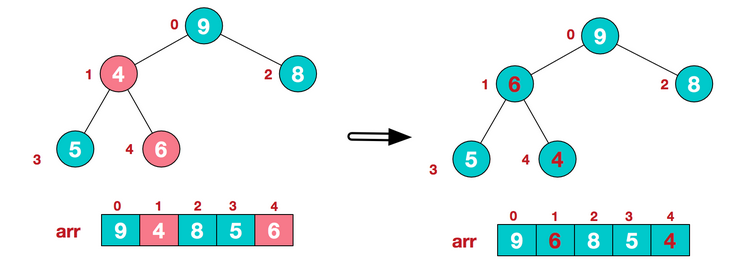
这部分代码如下:
void heap_sort::heapify(int Array[],int i,int n)//最大堆 { int child; for (; Lchild(i) < n; i = child)//这个for循环可以看出,heapify的思想是通过自顶向下的方法调整最大堆, { //并且只调整改变过位置的堆,这就要求下面的已经是最大(小)堆。 child = Lchild(i); //因为假如下面的树不符合堆的话,若上面的树已经形成堆了那么下面的就不会再作调整。 if (child + 1 < n&&Array[child] < Array[child + 1])//最终可能无法得出整个堆。 child++; if (Array[i] < Array[child]) { int temp = Array[i]; Array[i] = Array[child]; Array[child] = temp; } else break; } } void heap_sort::build_heap(int Array[], int n) { for (int i = n / 2; i >= 0; i--)//从最后的(往往是从没有子树的根节点开始,差不了多少)有子树的根节点开始。 { heap_sort::heapify(Array, i, n); } }
2. 交换堆顶与堆末尾的数值,并且调整堆的长度后,重新调整成最大(最小)堆,一直循环直至堆中只剩一个堆顶元素。这个过程实际上大部分人已经能理解了。如下图所示:
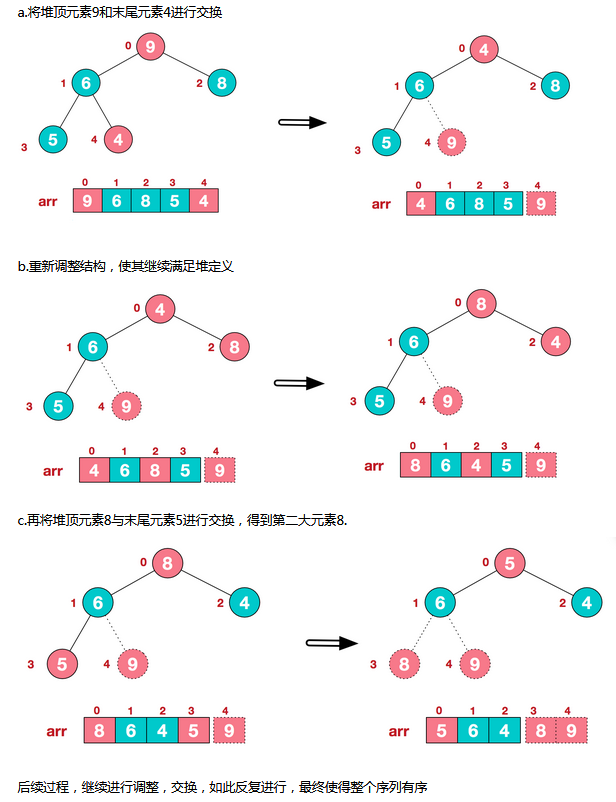
最终得到图如下:

这部分代码如下:
void heap_sort::sort_heap(int Array[], int n) { heap_sort::build_heap(Array, n); for (int i = n - 1; i > 0; i--) { int temp = Array[i]; Array[i] = Array[0]; Array[0] = temp; heap_sort::heapify(Array, 0, i);//因为下面的已经是堆,所以上面经过变换后变成无序树后只需要自顶向下调整即可。 } }
完整的工程代码如下:
Sort.h
//自己编写的各种排序算法的头文件。 #ifndef _SORT_H #define _SORT_H //冒泡排序 class bubble_sort{ private: int *Array,Length; public: bubble_sort(int *Array1,int Length); int *sort_bubble(); }; //归并排序 class merge_sort{ public: static void sort_merge(int Array1[], int Array2[], int Left, int Rightend, int Right,int recursion); static void Merge(int Array1[], int Array2[], int Left, int Rightend);//递归方法 static void Merge_pass(int Array1[], int Array2[], int ordered_len,int Length); static void Merge1(int Array1[], int Array2[], int Length);//非递归方法 }; //快速排序 class quick_sort{ public: static void sort_quick(int Array1[],int Left,int right); }; //插入排序 class insertion_sort{ public: static void sort_insertion(int Array[], int n); }; //堆排序 class heap_sort{ public: static void sort_heap(int Array[], int n); static void build_heap(int Array[], int n); static void heapify(int Array[], int i, int n); }; //选择排序 class selection_sort{ public: static void sort_selection(int Array[], int n); }; #endif
heap_sort.cpp
#include "Sort.h" #define Lchild(i) (2*i+1)//定义对于传入的根节点算出相应的左子节点 void heap_sort::heapify(int Array[],int i,int n)//最大堆 { int child; for (; Lchild(i) < n; i = child)//这个for循环可以看出,heapify的思想是通过自顶向下的方法调整最大堆, { //并且只调整改变过位置的堆,这就要求下面的已经是最大(小)堆。 child = Lchild(i); //因为假如下面的树不符合堆的话,若上面的树已经形成堆了那么下面的就不会再作调整。 if (child + 1 < n&&Array[child] < Array[child + 1])//最终可能无法得出整个堆。 child++; if (Array[i] < Array[child]) { int temp = Array[i]; Array[i] = Array[child]; Array[child] = temp; } else break; } } void heap_sort::build_heap(int Array[], int n) { for (int i = n / 2; i >= 0; i--)//从最后的(往往是从没有子树的根节点开始,差不了多少)有子树的根节点开始。 { heap_sort::heapify(Array, i, n); } } void heap_sort::sort_heap(int Array[], int n) { heap_sort::build_heap(Array, n); for (int i = n - 1; i > 0; i--) { int temp = Array[i]; Array[i] = Array[0]; Array[0] = temp; heap_sort::heapify(Array, 0, i);//因为下面的已经是堆,所以上面经过变换后变成无序树后只需要自顶向下调整即可。 } }
selection_sort.cpp
#include "Sort.h" void selection_sort::sort_selection(int Array[], int n) { for (int i = 0; i < n; i++) { int min_location = i; for (int j = n - 1; j >i; j--) { if (Array[j] < Array[min_location]) min_location = j; } int temp; temp = Array[min_location]; Array[min_location] = Array[i]; Array[i] = temp; } }
main.cpp
#include <iostream> #include "Sort.h" using namespace std; void main() { int Array[] = { 7, 5, 2, 1, 3, 7,93, 6,5, 10, 100, 98, 44, 66, 23 }; int Array2[] = { 7, 5, 2, 1, 3, 7, 93, 6, 5, 10, 100, 98, 44, 66, 23 }; int n = sizeof(Array) / sizeof(int); int n2 = sizeof(Array2) / sizeof(int); heap_sort::sort_heap(Array, n); selection_sort::sort_selection(Array2, n2); cout << "堆排序:" << endl; for (int i = 0; i < n; i++) { cout << Array[i] << endl; } cout << "选择排序:" << endl; for (int i = 0; i < n; i++) { cout << Array2[i] << endl; } system("pause"); }
运行结果如下:
到此介绍结束,欢迎交流。
作者: 十面埋伏但莫慌
出处: <https://www.cnblogs.com/leo-lv/>
转载请注明出处及原文链接,谢谢!



