Hbase 数据结构--跳跃表
简介
在HBASE中，跳跃表有是应用在MEM上做为查询有若干的平衡数据结构像：B树、红黑树、AVL树等，这类树在大的数据量存储上会有些性能上的瓶颈。
于是搜索理论，然后找B站学习了一下相关视频：
若干数据结构讲究CRUD操作，今天我们来简单地把这些原理性问题解释一下，看看跳跃表是如何实现这类操作的。
同时，跳跃表有各个版本，版本的逻辑细节上有些出入，大体都一样的，然后找了其他博客一些案例作为解释：
数据结构
先说一下这个常用的数据结构几个特点：
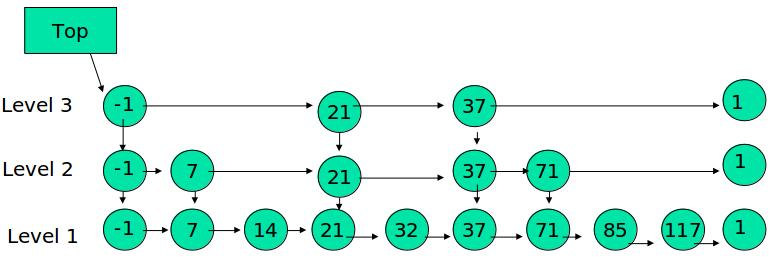
(1) 由很多层结构组成
(2) 最底层(Level 1)的链表是双向有序链表，上面每一层是单向有序链表
(3) 最底层(Level 1)的链表包含所有元素
(4) 除最底层(Level 1)的链表，上面的元素如果一个元素出现在 Level i 的链表中，则它在 Level i 之下的链表也都会出现。
(5) 每个节点包含两个指针，一个指向同一链表中的下一个元素，一个指向下面一层的元素。
C：增加
C也就是我们说的增加数据
STEP1：产生随机数
1 import random 2 3 def random_level(): 4 k = 1 5 while random.randint(0,1): 6 k += 1 7 return k
用这个随机数来决定当前增加的层级，如果为真则增加一层，直到停止； 注：有些表的操作是直接加入层级，比如k = 1 就将增加上一层或Kn层，根据随机数来决定增加几层。
STEP2：插入
利用前面生面的层级k ,决定插入的层级数，这里引用了别人的案例；
例子：插入 119， K = 2
如果 K 大于链表的层数，则要添加新的层。
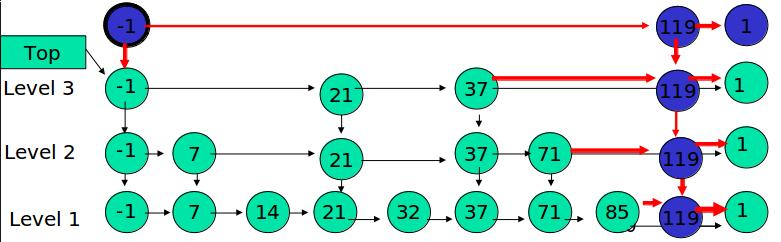
例子：插入 119， K = 4
R：删除
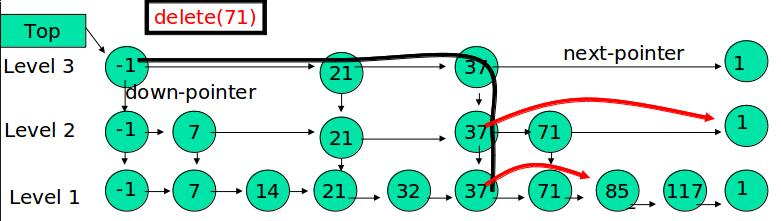
删除还是比较容易的，跳跃树有一个特点，就是第一层是双面链表，上面的层级都是单向链表，所以只需修改链表指针即可实现删除操作；
例子：删除 71
U：更新
更新的操作实际就是二个操作，即增加+删除操作。
当数据存在我们的列表中，则直接更新即可以。
如果数据不在我们的列表中，先将列表元素删除，然后增加，最后将指针修正正确。
D：搜索
搜索就so easy了，从最顶层开始找，找不到就下沉一层一直找到为止，当然有可能找不到；
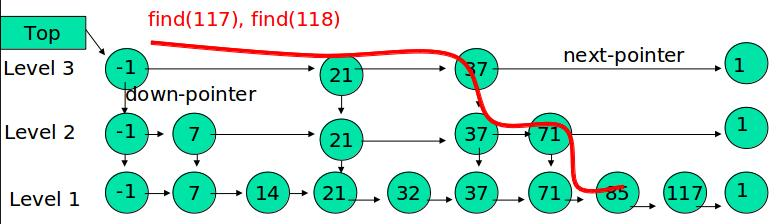
例子：查找元素 117
(1) 比较 21， 比 21 大，往后面找
(2) 比较 37, 比 37大，比链表最大值小，从 37 的下面一层开始找
(3) 比较 71, 比 71 大，比链表最大值小，从 71 的下面一层开始找
(4) 比较 85， 比 85 大，从后面找
(5) 比较 117， 等于 117， 找到了节点。
ref : https://www.cnblogs.com/thrillerz/p/4505550.html
