word2vec原理

一、统计语言模型

统计语言模型就是指计算一个句子出现概率的模型。假设一句话由T个词按顺序构成，则这T个词的联合概率就是这个句子的概率：

$$p(W)=p(w_1^T)=p(w_1,w_2,\ldots,w_T)$$

利用贝叶斯公式，上式可写为：

$$p(W)=p(w_1^T)=p(w_1)p(w_2|w_1)p(w_3|w_1^2)\cdots p(w_T|w_1^{T-1})=\prod_{t=1}^{T}p(w_t|w_1^{t-1})$$

其中的条件概率便是模型的参数，参数个数为T个。当语料库（Corpus）C足够大的时候，条件概率$p(w_t|w_1^{t-1})=\frac{p(w_1^t)}{p(w_1^{t-1})}$可表示为：

$$p(w_t|w_1^{t-1})=\frac{p(w_1^t)}{p(w_1^{t-1})} \approx  \frac{count(w_1^t)}{count(w_1^{t-1})}$$

假设词汇表为V，其中词汇的个数是$|V|$，那么对于一个长度为T的句子，有$|V|^T$种组合方式，对于每一种组合方式，都要计算T个参数，总共就需要计算$T|V|^T$个参数，计算量非常之大，所以该模型并不容易实现。

 

二、n-gram模型

n-gram模型对条件概率$p(w_t|w_1^{t-1})$做了一个Martov假设，认为一个词出现的概率只和它前面的n-1个词相关，可表示为：
$$p(w_t|w_1^{t-1}) \approx p(w_t|w_{t-n+1}^{t-1})$$
当n=2时：
$$p(w_t|w_1^{t-1}) \approx p(w_t|w_{t-1}) \approx \frac{count(w_{t-1},w_t)}{count(w_{t-1})}$$

这时单个参数$p(w_t|w_1^{t-1})$的统计就变得简单了。
在模型效果方面，n=2再到n=3，模型效果上升显著，从n=3到n=4时，模型效果提升不明显。

 

三、神经概率语言模型

从上面的模型可以看到，问题的核心在于找到一个方法去计算$p(w_t|w_1^{t-1})$，神经概率语言模型的方法是通过一个神经网络去学习这个概率，具体为：
1、将词汇表V中的任意一个词$i$通过映射关系C将其映射为一个m维实数向量$C(i) \in R^m$，其中C由$|V|\times m$维矩阵来表示
2、对于词汇表中的第$i$个词$i=w_t$，给定其上下文环境对应的特征向量：
$$Context=(C(w_{t-1}),C(w_{t-2}),\ldots,C(w_{t-n+1}))$$

则在Context出现的情况下，$w_t$出现的条件概率可用概率函数来表示：
$$f(i,w_{t-1},\dots,w_{t-n+1})=g(i,C(w_{t-1}),C(w_{t-2}),\ldots,C(w_{t-n+1}))$$

其中映射关系C的参数就是词的特征向量本身，由$|V|\times m$维矩阵来表示，其中第i行的就是词汇表V中第i个的特征向量C(i)，函数g可认为是一个前馈或递归神经网络.
对于任意的上下文词组，在该词组出现的条件下，有如下约束：
$$\sum_{i=1}^{|V|}f(i,w_{t-1},\dots,w_{t-n+1})=1$$
即在该上下文词组出现的情况下，下一个词必然出现在词汇表中，所以其加和为1，不同的词出现的概率不一样。

 

 

该模型的结构如下图所示：

 

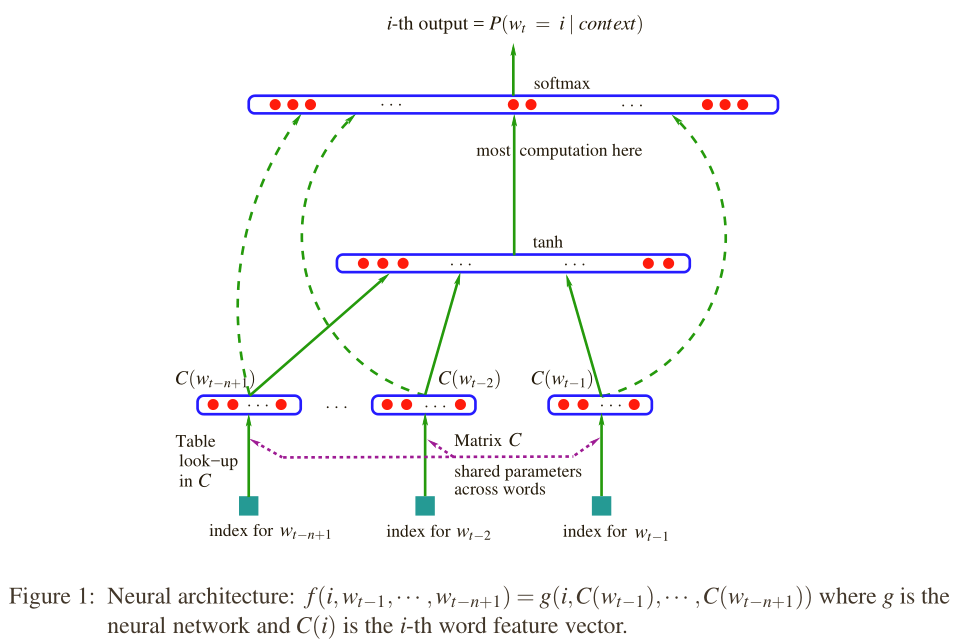
最下面表示的是上下文词组在词汇表中的索引，输入x即为上下文词组的特征向量，即将n-1个词的向量首尾连接起来，维度为$(n-1)\times m$：
$$x=Context=(C(w_{t-1}),C(w_{t-2}),\ldots,C(w_{t-n+1}))$$

这个是输入层，中间层是一个隐藏层，具体为双曲正切函数$tanh$，隐藏层的输出为：
$$y=b+U tanh(d+Hx)$$

其中，H是一个$h \times (n-1)m$的一个矩阵，其中h为隐藏层的神经元个数，d为隐藏层的偏移（共有h个元素），U是隐藏层输出的权重矩阵（$|V| \times h$），b是隐藏层输出的偏移。
可以得到模型中的参数为：
$$\theta=(b,d,U,H,C)$$

参数的个数为：
$$|V|(1+nm+h)+h(1+(n-1)m)$$

在输出层用softmax函数将概率归一化，具体为：
$$p(w_t|w_{t-1},\ldots,w_{t-n+1})=\frac{e^{y_{w_t}}}{\sum_{i \in V} e^{y_i}}$$

其物理意义表示在给定上下文词组的条件下，输出$w_t$为词汇表V中的第i个词（索引）的概率。

目标是最大化对数似然函数：
$$L=\frac{1}{T} \sum_t log f(w_t,w_{t-1},\ldots,w_{t-n+1};\theta)$$

为了求得最优的参数$\theta$，即可使用随机梯度上升法：

$$\theta \leftarrow \theta + \frac {\partial  log  p(w_t|w_{t-1},\ldots,w_{t-n+1})}{\partial \theta}$$

 

四、word2vec

 word2vec是在上面的模型基础上发展而来的，包括两个模型，CBOW模型(Continuous Bag-of-Words Model)和Skip-gram模型(Continuous Skip-gram Model)。可分别基于Hierarchical Softmax和Negative Sampling来设计，下面只介绍Hierarchical Softmax的CBOW和Skip-gram模型。

 

1、CBOW

与神经概率语言模型类似，CBOW模型同样包括三层神经网络结构，输入层，投影层，和输出层。

其中每一个样本形式为(Context(w),w)，其中Context(w)为w的上下文环境，由词w前后各c各词组成。

输入层：Context(w)中2c个词的词向量

投影层：将2c个词向量做加和

$$x_{w_t}=\sum_{i=1}^{2c}C(w_i) \in R^m$$

输出层：一棵Huffman树，叶子节点共$|V|$个，$|V|$表示词汇表V的大小

 

该模型与神经概率语言模型有如下不同：

1、神经概率语言模型的输入层是上下文词组拼接而成，而CBOW是累加得到

2、神经概率语言模型有隐藏层$tanh$，而CBOW没有

3、神经概率语言模型输出的是线性结构，而CBOW的输出是树形结构Huffman树

 

未完待续