漫步支持向量机(svm)之二 拉格朗日乘子法

所谓工欲善其事，必先利其器，要想求解目标函数的最小值，而且还是在有不等式约束条件下的最小值，就必须要知道拉格朗日乘子法。

设目标函数为
$$
J(x,y)=x^2+y^2
$$

则求$J(x,y)$的最小值很简单吧，让J关于x，y的偏导数等于0，即可求出最小点$\hat x,\hat y$,$J(x,y)$的几何图像是一个抛物面，其等值面则是以原点为中心的同心圆环。

那如果加上约束线$y=x^2+1$，那也就意味着，自变量$x,y$只能在约束线上运动。几何图像如下所示：

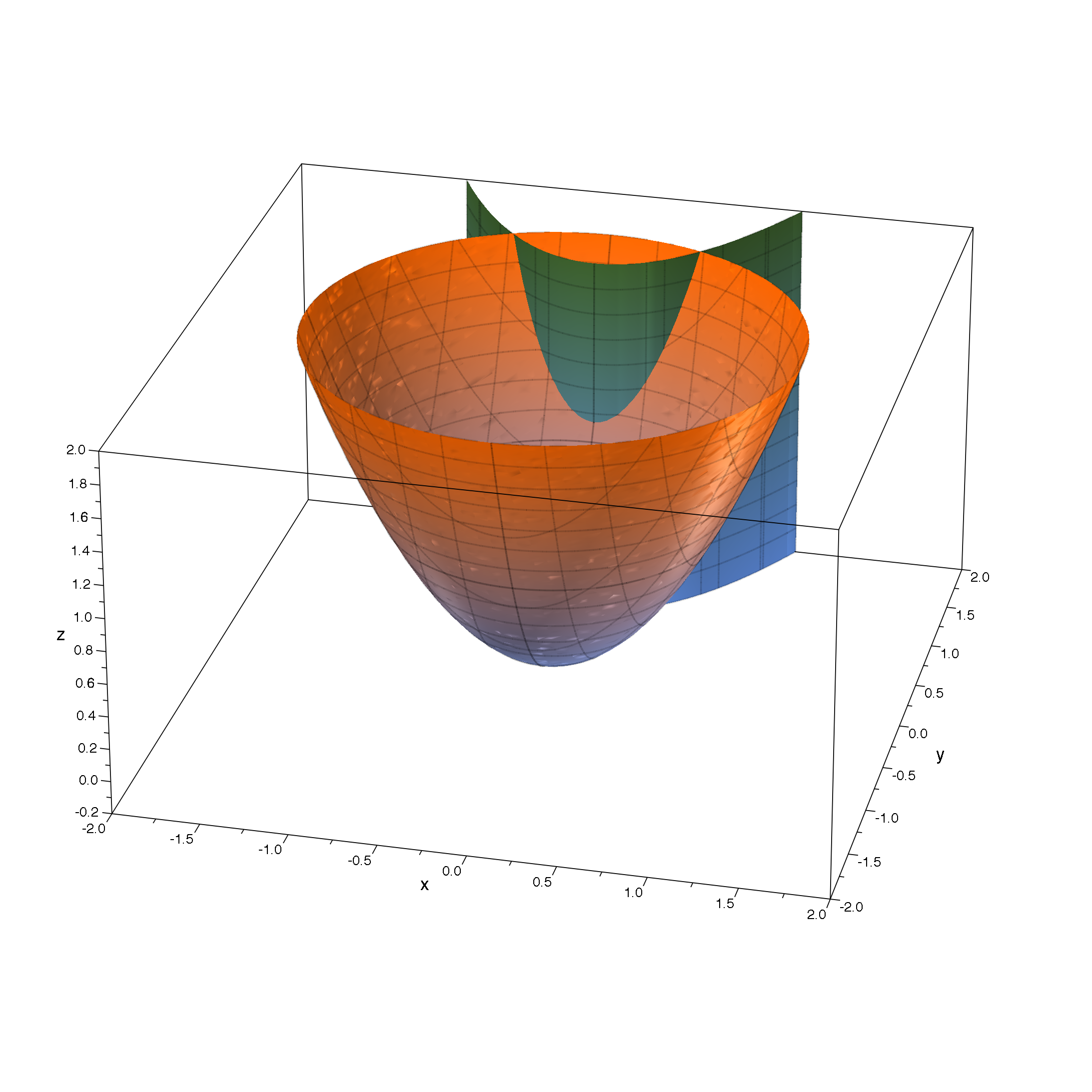
等高线图像如下：

此时求目标函数$J(x,y)$的最小值就不在J关于x,y偏导为0的点上了，因为关于x,y偏导为0的点不在约束线上。

仔细观察$J(x,y)$的等值面，可以发现从原点往外，等值面所对应的目标函数的值一直在增加，等值面与约束线的关系有三种，相交，相切，相离。相交表示自变量可以取到约束线上的值，相切的时候正好处于临界位置，此时也是目标函数在约束线上取到极值的时候，相离表示自变量不在约束线上，纵然此时目标函数可能取到更小的值，然而已经在约束线之外了，并没有什么卵用。

好了，既然相切的时候就是目标函数在约束条件下取到最小值的时候，那就好办了，相切意味着等值面（在二维情况下应该叫做等高线更合适些）的法向量和约束线的法向量在切点处共线。

也就是说，等高线$J(x,y)=x^2+y^2=R^2$的梯度向量$\nabla J=(\partial J/\partial x,\partial J/\partial y)$和约束线$C(x,y)=x^2+1-y=0$的梯度向量$\nabla C=(\partial C/\partial x,\partial C/\partial y)$共线。也即
$$
\nabla J+\lambda \nabla C=0
$$
其中的$\lambda$就是传说中的拉格朗日乘子了。

有了这个等式，再加上约束线方程，就可以解出极值点和拉格朗日乘子$\lambda$了。

好了，如果是不等式约束又该如何求解呢？

此时要分两种情况来讨论，第一种情况是当极值点就在约束线上时，这个时候其实等价于等式约束，也即和$C(x,y)=0$时的极值点是一样的。比如不等式约束为：
$$C(x,y)=x^2+1-y \le 0$$
如图所示：

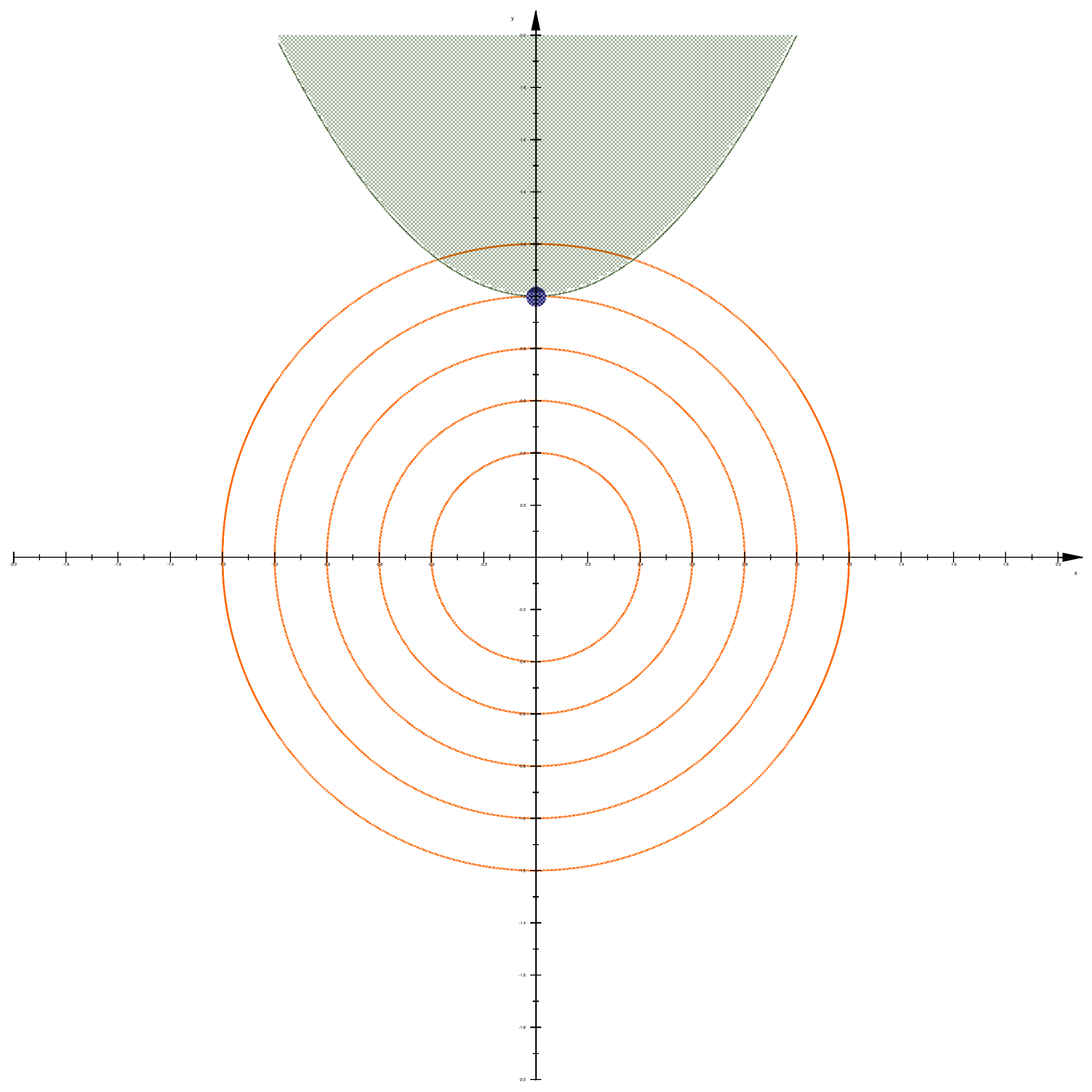
第二种情况是当极值点不在约束线上，此时极值点在哪儿呢？当然在$J(x,y)$关于$x,y$的偏导为0的点上了，此时约束条件并不起作用，也就是说拉格朗日乘子等于0。比如不等式约束为：
$$C(x,y)=-x^2-1+y \le 0$$
如图所示：

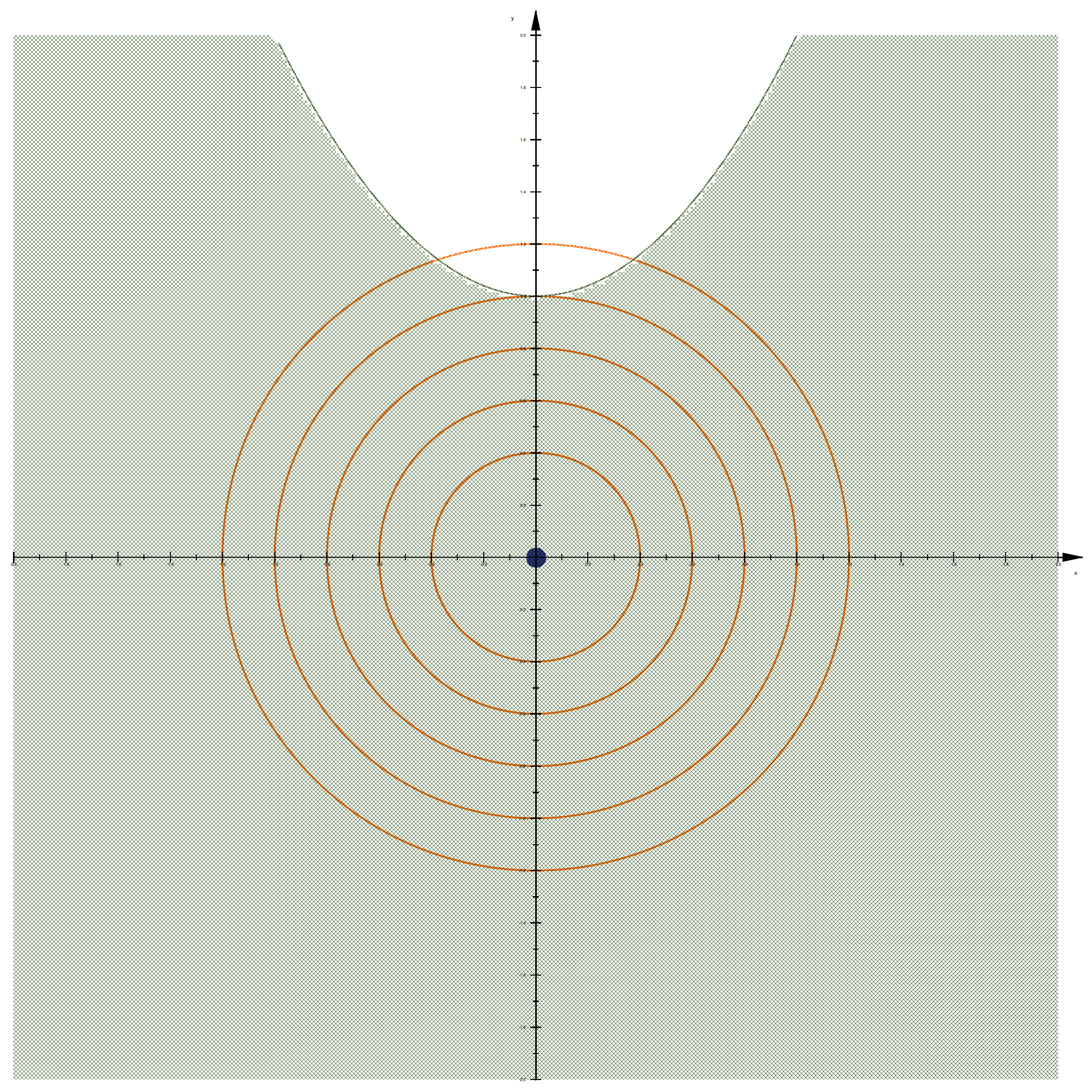
将上面两种情况结合在一起，可以写成：
$$
\lambda \cdot C(x,y)=0
$$

也就是说，当$\lambda=0$时，极值点不在约束线上，而在$C(x,y)<0$的地方，也就是$\nabla J(x,y)=0$的地方，此时等价于无约束条件下求解目标函数数的极值。当$C(x,y)=0$时，极值点在约束线上，此时等价于等式约束，而且目标函数的梯度$\nabla J$与约束线的梯度$\nabla C$反向，因为约束面在$C(x,y) \le 0$的区域，而梯度$\nabla C$指向的是$C(x,y)$增加的方向，所以在方程$\nabla J+\lambda \nabla C=0$中$\lambda$要大于等于0。

若设拉格朗日函数为：
$$
L(x,y,\lambda)=J(x,y)+\lambda \cdot C(x,y)
$$

那么$\nabla J+\lambda \nabla C=0$可以写成$\nabla L=0$

好了，总结一下，要求解不等式约束下目标函数的极值，并假设极值点为$(\hat x,\hat y)$，相应的拉格朗日乘子为$\hat \lambda$ ,那么需要满足以下条件：

$$
\nabla L=\nabla J+\hat \lambda \nabla C=0 \\
C(\hat x,\hat y) \le 0\\
\hat \lambda \cdot C(\hat x,\hat y)=0 \\
\hat \lambda \ge 0
$$

这个条件也就是传说中的KKT条件。