Hangover(1.4.1)

Description

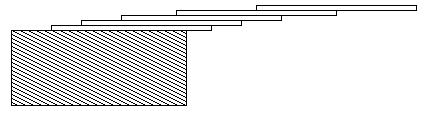
How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

#include <iostream>
#include<cmath>
using namespace std;
int main()
{double n;
int i;
while(cin>>n&&n!=0.00){
	double a=0.00;

for(i=2;i<10000;i++)
{a=a+double(1.0/i);
if(a>=n)break;}
cout<<i-1<<" card(s)"<<endl;

}

return 0;}

注意要用0.1对double类型进行乘除