栈（Stack）和队列

栈（Stack）和队列

栈是一个后进先出的线性表，它要求只在表尾进行删除和插入操作。

所谓的栈，其实就是一个特殊的线性表。表尾称为栈顶（Top），相应的表头称为栈底（Bottom）。

栈的插入（Push）,栈的删除（Pop）.最开始栈中不包含任何数据，称为空栈，此时栈顶就是栈底，然后数据从栈顶进入，栈顶和栈底分离。数据出栈时从栈顶弹出，栈顶下移，整个栈的当前容量变小。

 

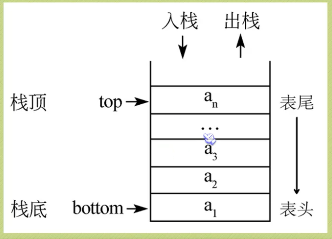
入栈操作在栈顶进行，每次向栈中压入一个数据，top指针加1，直到栈满为止。

出栈操作就是在栈顶取出数据，栈顶指针下移，栈的当前容量-1。

 

 逆波兰表达式：（没有括号）逆波兰表达式又叫做后缀表达式，是一种没有括号，并严格遵循“从左到右”运算的后缀式表达方法。

 它的优势在于只用两种简单操作，入栈和出栈就可以搞定任何普通表达式的运算。其运算方式如下：

如果当前字符为变量或者为数字，则压栈，如果是运算符，则将栈顶两个元素弹出作相应运算，结果再入栈，最后当表达式扫描完后，栈里的就是结果。

16：队列（queue)

只允许在一端进行插入操作，而在另一端进行删除操作的线性表。与栈相反，队列是一种先进先出的线性表。实现一个队列同样需要顺序表或链表作为基础。

 

队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

 

队列既可以用链表实现，也可以用顺序表实现。但和栈相反，栈一般我们通过顺序表实现，而队列我们常通过链表实现，称为链队列。

 创建一个队列：首先在内存中创建一个头节点，然后将队列的头指针和尾指针都指向这个生成的头结点，此时为空队列。

队列的顺序存储结构：假设一个队列有n个元素，则顺序存储的队列需要建立一个大于n的存储单元，并把队列的所有元素存储在数组的前n个单元，数组下标为0的一端是队头。

 如果队头指针可以移动，那么出队列复杂度就可以下降。但要解决假溢出的问题。循环队列,取模操作。